- •Ргр «Математический анализ» з а д а ч а 1
- •Контрольные варианты к задаче 1
- •З а д а ч а 2
- •Контрольные варианты к задаче 2
- •З а д а ч а 3
- •Контрольные варианты к задаче 3
- •З а д а ч а 4
- •Контрольные варианты к задаче 8
- •З а д а ч а 9
- •Контрольные варианты к задаче 9
- •З а д а ч а 10
- •Контрольные варианты к задаче 10
- •З а д а ч а 11
- •Контрольные варианты к задаче 11
- •З а д а ч а 12
- •З а д а ч а 15
- •Контрольные варианты задачи 15
- •З а д а ч а 16
- •Контрольные варианты задачи 16
- •Образец выполнения контрольной работы
- •Образец выполнения контрольной работы
- •«Графики функций»
- •Задача №27. Построить графики функций, заданных параметрически,
- •Указания к выполнению
- •Образец выполнения контрольной работы
Образец выполнения контрольной работы
“ Функции нескольких переменных ”
1)
Найти
 и
и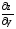 функции
функции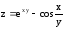 .
.
Решение
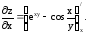 Считаем переменную “y”
постоянной величиной.
Считаем переменную “y”
постоянной величиной.
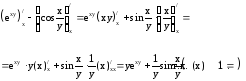
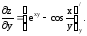 Считаем
переменную “х” постоянной величиной.
Считаем
переменную “х” постоянной величиной.
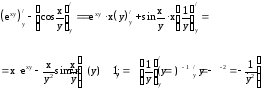
Ответ:
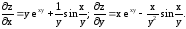
2)
Показать, что
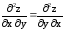 при
при .
.
Решение. Сначала найдем первые частные производные
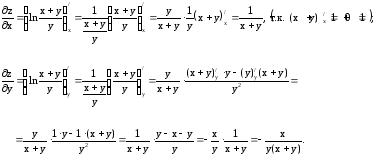
Теперь находим смешанные вторые частные производные и сравниваем их.
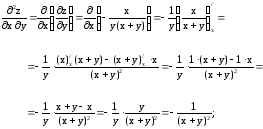
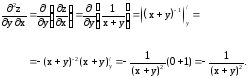
Видим, что смешанные производные равны, что и требовалось доказать.
3)
Вычислить приближенно с помощью
дифференциала
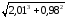 .
.
Решение.
Введем
функцию двух переменных
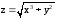 .
Так как 2,01=2+0,01,
.
Так как 2,01=2+0,01,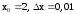 .
Аналогично
.
Аналогично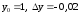 ,
т. к.
,
т. к.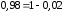 .
Воспользуемся тем, что
.
Воспользуемся тем, что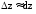 при малых
при малых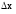 и
и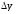 .
.
Так
как
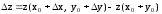 ,
,
отсюда
следует, что
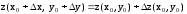 .
.
Заменим
приращение функции
 ее дифференциалом
ее дифференциалом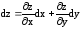 ,
,
где
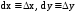 .
.
Тогда
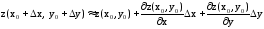 ,
,
т.
е. в данном случае
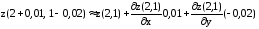 .
.
Вычислим
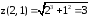 .
Найдем
.
Найдем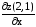 .
Для этого сначала найдем частную
производную
.
Для этого сначала найдем частную
производную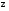 по
по в произвольной точке.
в произвольной точке.

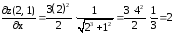 .
.
Теперь найдем
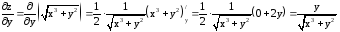 ;
;
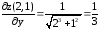 .
.
Находим искомое значение корня
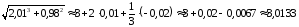 .
.
Если
найти
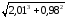 на калькуляторе, то получим
на калькуляторе, то получим .
Различие только в четвертом знаке после
запятой.
.
Различие только в четвертом знаке после
запятой.
Ответ:
 .
.
4)
Исследовать на экстремум функцию
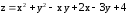 .
.
Решение. Найдем сначала стационарные точки, т. е. те точки, в которых частные производные одновременно равны нулю:

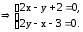
Изменим порядок во втором уравнении и приведем систему линейных уравнений к стандартному виду, чтобы ее можно было решить методом Крамера.
 .
.
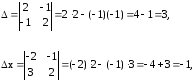

Нашли
одну стационарную точку, в которой
 ,
это точка
,
это точка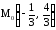 .
.
Выясним
с помощью вторых производных, есть ли
в
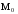 экстремум, и, если есть, какой.
экстремум, и, если есть, какой.
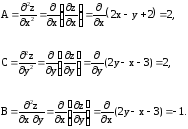
Составляем
определитель
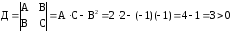 .
.
Так
как
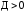 ,
экстремум существует. Так как
,
экстремум существует. Так как ,
в стационарной точке
,
в стационарной точке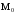 функция имеет минимум. Найдем его.
функция имеет минимум. Найдем его.
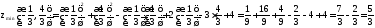 .
.
Ответ:
 .
.
5)
Найти наибольшее и наименьшее значения
функции
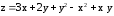 в треугольнике со сторонами
в треугольнике со сторонами .
.
Решение. Так как свои наибольшее и наименьшее значения непрерывная функция может иметь или в стационарной точке внутри рассматриваемой области или на границе этой области, задачу будем решать в два действия. Найдем стационарные точки и значения функции в тех из них, которые лежат в рассматриваемой области.
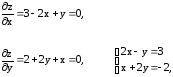
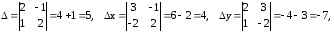
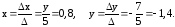
2
В
1
Д
А С
0 1 2 х
М0

Точка
 не принадлежит треугольнику
не принадлежит треугольнику (рис. 7), поэтому значение функции в этой
точке не вычисляем. Переходим ко второму
действию. Треугольник
(рис. 7), поэтому значение функции в этой
точке не вычисляем. Переходим ко второму
действию. Треугольник ограничивают три прямые. Будем
исследовать функцию на экстремум на
каждой из них. Сначала найдем значения
функции в вершинах треугольника.
ограничивают три прямые. Будем
исследовать функцию на экстремум на
каждой из них. Сначала найдем значения
функции в вершинах треугольника.




Рисунок 7
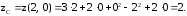
Рассмотрим
границу
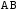 :
: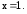 Подставляя
Подставляя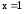 в выражение функции, получим
в выражение функции, получим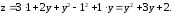
Получили
задачу на экстремум для функции одной
переменной. Найти наибольшее и наименьшее
значения функции
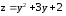 на отрезке
на отрезке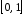 .
Находим
.
Находим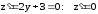 при
при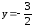 ,
а это значение
,
а это значение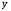 не входит в рассматриваемый отрезок
не входит в рассматриваемый отрезок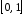 .
На концах отрезка значения функции
уже подсчитаны, это
.
На концах отрезка значения функции
уже подсчитаны, это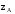 и
и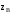 .
.
Переходим
к границе
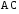 :
: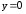 .
Подставляя
.
Подставляя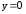 в выражение функции, получим
в выражение функции, получим .
.
Снова
решаем задачу для функции одной
переменной. Найти наибольшее и наименьшее
значения функции
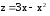 на отрезке
на отрезке .
.
Находим
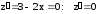 при
при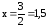 .
Эта точка входит в отрезок
.
Эта точка входит в отрезок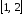 .
Поэтому вычислим значение функции в
этой точке.
.
Поэтому вычислим значение функции в
этой точке.
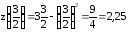 .
.
На
концах отрезка значения функции
подсчитаны заранее, это
 и
и .
.
Рассматриваем
третью границу
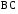 :
: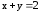 .
Выразим
.
Выразим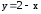 и подставим в выражение функции:
и подставим в выражение функции:
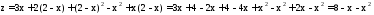 .
.
Ищем
наибольшее и наименьшее значения функции
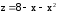 на отрезке
на отрезке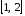 .
.
Находим
 при
при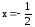 ,
а это значение
,
а это значение не входит в
не входит в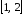 .
Теперь выбираем из найденных значений
функции
.
Теперь выбираем из найденных значений
функции наибольшее. Это значение равно 6 в точке
наибольшее. Это значение равно 6 в точке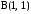 .
А наименьшее значение принимается в
двух точках:
.
А наименьшее значение принимается в
двух точках: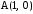 и
и .
.
Ответ:
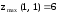 ,
, .
.
6)
Найти производную функции
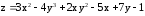 в точке
в точке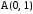 в направлении от этой точки к точке
в направлении от этой точки к точке .
.
Решение.
Напишем
формулу производной функции по
направлению вектора
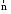 .
.
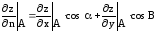 ,
,
где
 – орт направления вектора
– орт направления вектора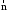 .
.
Сначала
найдем вектор
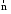 ,
в направлении которого будем искать
производную.
,
в направлении которого будем искать
производную.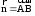
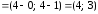 .
Найдем длину
.
Найдем длину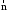 .
.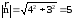 .
Направляющие косинусы вектора
.
Направляющие косинусы вектора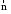 совпадают с координатами орта
совпадают с координатами орта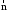 ,
поэтому
,
поэтому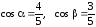 .
.
Теперь
найдем частные производные функции
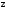 .
.
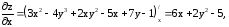

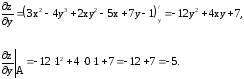
Все найденные значения подставляем в формулу производной по направлению:
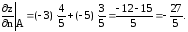
Вывод.
Функция
 убывает по направлению вектора
убывает по направлению вектора ,
так как полученная производная меньше
нуля.
,
так как полученная производная меньше
нуля.
Ответ: