З а д а ч а 15
Известно,
если
.
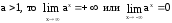Пример 17
Исследовать
функцию
на непрерывность. Установить характер
точек разрыва. Схематично построить
график функции .
Функция
элементарная, поэтому она непрерывна
во всех точках, кроме точки
,
где она не определена.
,
.
Поэтому
,
.
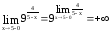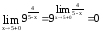В точке
-
разрывII
рода, т. к. левосторонний предел бесконечен.
Контрольные варианты задачи 15
Исследовать
функцию
на непрерывность. В точках разрыва
установить характер разрыва. Схематично
построить график функции:
|
1.
|
2.
|
3.
|
4.
|
5.
|
|
6.
|
7.
|
8.
|
9.
|
10.
|
|
11.
|
12.
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
19.
|
20.
|
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
26.
|
27.
|
28.
|
29.
|
30.
|
З а д а ч а 16
По
определению модуль числа
Следовательно,
Пример 18
Исследовать функцию на непрерывность. Установить характер разрыва. Построить график функции
.
так
как
Функция
не определена в точке
.
Эта функция может быть записана в виде
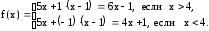
Каждое
из аналитических выражений непрерывно,
следовательно, функция
имеет разрыв только в точке
,
где она не определена. Слева от этой
точки
функция
задана формулой
.
Следовательно,
=
.
Справа от точки
функция задана формулой
,
поэтому
.
Односторонние пределы в точке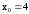
конечны, но не равны между собой. Предел
функции в точке
не существует. Функция имеет разрыв в
этой точке, который является неустранимым
разрывомI
рода (скачком).
Контрольные варианты задачи 16
Исследовать функцию на непрерывность. В точках разрыва установить характер разрыва. Схематично построить график функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
“ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ”
17. Найти производные функций:
|
1. |
1)
|
2)
|
3)
| |
|
4)
|
5)
|
6)
| ||
|
7)
|
8)
|
9)
| ||
|
10)
|
| |||
|
| ||||
|
2. |
1)
|
2)
|
3)
| |
|
4)
|
5)
|
6)
| ||
|
7)
|
8)
|
9)
| ||
|
10)
|
| |||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
|
3. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
4. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
5. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
6. |
1)
|
2)
|
3)
| ||
|
4)
|
5)
|
6)
| |||
|
7)
|
8)
|
9)
| |||
|
10)
|
| ||||
|
7. |
1)
|
2)
|
3)
| ||
|
4)
|
5)
|
6)
| |||
|
7)
|
8)
|
9)
| |||
|
10)
|
| ||||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
|
8. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
9. |
1)
|
2)
|
3)
| ||||
|
4)
|
5)
|
6)
| |||||
|
7)
|
8)
|
9)
| |||||
|
10)
|
| ||||||
|
| |||||||
|
10. |
1)
|
2)
|
3)
| ||||
|
4)
|
5)
|
6)
| |||||
|
7)
|
8)
|
9)
| |||||
|
10)
|
| ||||||
|
| |||||||
|
11. |
1)
|
2)
|
3)
| ||||
|
4)
|
5)
|
6)
| |||||
|
7)
|
8)
|
9)
| |||||
|
10)
|
| ||||||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
|
12. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
13. |
1)
|
2)
|
3)
| ||
|
4)
|
5)
|
6)
| |||
|
7)
|
8)
|
9)
| |||
|
10)
|
| ||||
|
| |||||
|
14. |
1)
|
2)
|
3)
| ||
|
4)
|
5)
|
6)
| |||
|
7)
|
8)
|
9)
| |||
|
10)
|
| ||||
|
15. |
1)
|
2)
|
3)
| ||
|
4)
|
5)
|
6)
| |||
|
7)
|
8)
|
9)
| |||
|
10)
|
| ||||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
|
16. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
17. |
1)
|
2)
|
3)
| |
|
4)
|
5)
|
6)
| ||
|
7)
|
8)
|
9)
| ||
|
10)
|
| |||
|
| ||||
|
18. |
1)
|
2)
|
3)
| |
|
4)
|
5)
|
6)
| ||
|
7)
|
8)
|
9)
| ||
|
10)
|
| |||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
|
19. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
20. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
21. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
22. |
1)
|
2)
|
3)
| |
|
4)
|
5)
|
6)
| ||
|
7)
|
8)
|
9)
| ||
|
10)
|
| |||
|
23. |
1)
|
2)
|
3)
| |
|
4)
|
5)
|
6)
| ||
|
7)
|
8)
|
9)
| ||
|
10)
|
| |||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
|
24. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
25. |
1)
|
2)
|
3)
| |||||
|
4)
|
5)
|
6)
| ||||||
|
7)
|
8)
|
9)
| ||||||
|
10)
|
| |||||||
|
| ||||||||
|
26. |
1)
|
2)
|
3)
| |||||
|
4)
|
5)
|
6)
| ||||||
|
7)
|
8)
|
9)
| ||||||
|
10)
|
| |||||||
|
| ||||||||
|
27. |
1)
|
2)
|
3)
| |||||
|
4)
|
5)
|
6)
| ||||||
|
7)
|
8)
|
9)
| ||||||
|
10)
|
| |||||||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
|
28. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
| |
|
7)
|
8)
|
9)
| |
|
10)
|
| ||
;
;
;
;
;
;
;
;
;
.
|
29. |
1)
|
2)
|
3)
| ||
|
4)
|
5)
|
6)
| |||
|
7)
|
8)
|
9)
| |||
|
10)
|
| ||||
|
| |||||
|
30. |
1)
|
2)
|
3)
| ||
|
4)
|
5)
|
6)
| |||
|
7)
|
8)
|
9)
| |||
|
10)
|
| ||||
|
10)
|
| ||||
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;
;
;
;
.
.
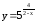
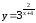
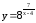
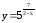
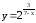
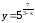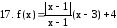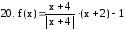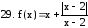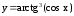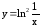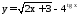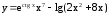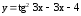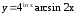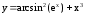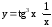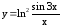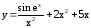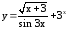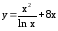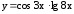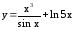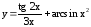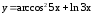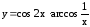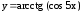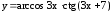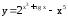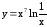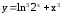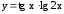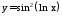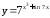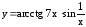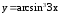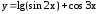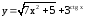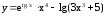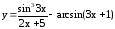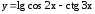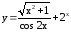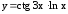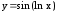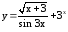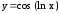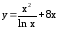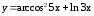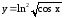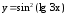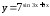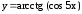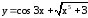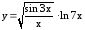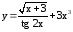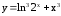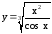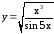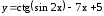