64. Какие напряжения возникают в поперечном сечении бруса круглого сечения при кручении и как они направлены?

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:

- все образующие поворачиваются на один и тот же угол , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

- каждое сечение поворачивается относительно другого на некоторый угол , называемый углом закручивания;

- радиальные линии на торцевой поверхности остаются прямыми.

На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.

Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где М_к=T (рис.5.5). На элементарной площадке dF будет действовать элементарная сила , момент который относительно оси вала равен. Крутящий моментМ_к, в сечении равен

.                                     (5.3)

                                                  Рис.5.5

 

Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной (рис.5.6).

Правый торец элемента повернется относительно левого на угол , образующаяСВ повернется на угол и займет положениеСВ₁. Угол - относительный сдвиг. Из треугольникаОВВ₁ найдем:

                                Рис.5.6                                                           Рис.5.7

 

.

 Из треугольника СВВ₁: . Откуда, приравнивая правые части, получим

.

На основании закона Гука при сдвиге:

.                                     (5.4)

Подставим выражение (5.2) в (5.1):

.

Откуда

.                                                  (5.5)

70. Как строятся эпюры поперечных сил и изгибающих моментов

Рассмотрим пример построения эпюр поперечных сил Q и изгибающих моментов M_x.

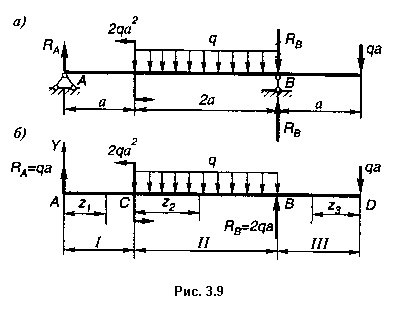
1. Изображаем расчетную схему (рис. 3.9, а).

2. Определяем реакции опор. Первоначально выбираем произвольное направление реакций (рис. 3.9, а) 

Так как реакция R_B с минусом, изменяем выбранное направление на противоположное (рис. 3.9, б), а про минус забываем.

Проверка: 

Y = 0,  R_A - 2qa + R_B - qa = qa - 2qa + 2qa - qa = 0.

3. Расчетная схема имеет три силовых участка.

I участок АС: 0 < z₁ < a. Начало координат выбираем в крайней левой точке А. Рассмотрим равновесие отсеченной части бруса (рис. 3.10).

В сечении возникают внутренние усилия:

поперечная сила 

Q = qa = const

и изгибающий момент 

M_x = qa * z₁ при z₁ = 0 M_x = 0; при z₁ = a M_x = qa².

II участок CB: 0 < z₂ < 2a. Начало координат перенесено в начало участка С (рис. 3.11).

На этом участке 

при z₂ = 0 Q = qa, M_x = -qa²;

при z₂ = 2 Q = -qa, M_x = qa². 

 

На 2-м участке в уравнении моментов аргумент z₂ имеет 2-ю степень, значит эпюра будет кривой второго порядка, т.е. параболой. На этом участке поперечная сила меняет знак (в начале участка +qa, а в конце -qa), значет на эпюре M_x будет экстремум в точке, Q = 0. Определяем координату сечения, в котором экстремальное значение M_x, приравнивая нулю выражение поперечной силы на этом участке. 

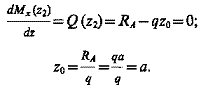
Определяем величину экстремального момента (с учетом знака):

III учаток BD: 0 < z₃ < a. Начало координат на третьем участке помещено в крайней правой точке (рис. 3.12). 

Здесь Q = qa = const; M_x = -qa*z₃; при z₃ = 0 M_x = 0; при z₃ = a M_x = -qa².

4. Строим эпюры Q и M_x (рис. 3.13, б и в). 

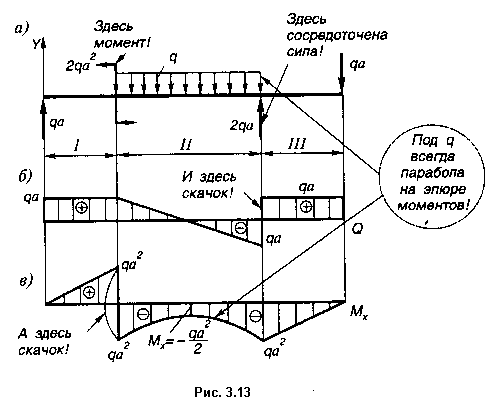
5. Проверка построения.