4°. Директрисы эллипса и гиперболы.
Рассмотрим какой-нибудь эллипс и введём декартову прямоугольную систему координат так, чтобы этот эллипс определялся каноническим уравнением
.
Предположим, что
рассматриваемый эллипс не является
окружностью, т.е. что
и, следовательно,
.
Предположим ещё, что этот эллипс вытянут
в направлении оси
,
т.е. что
.
Определение 6.
Две прямые, перпендикулярные к большой
оси эллипса и расположенные симметрично
относительно центра на расстоянии
от него, называются директрисами
эллипса.
Уравнение директрис в выбранной системе координат имеют вид
и
.
Первую из них мы условимся называть левой, вторую – правой.
Так как для эллипса
,
то
.
Отсюда следует, что правая директриса
расположена правее правой вершины
эллипса; аналогично, левая директриса
расположена левее его левой вершины.
Эллипс вместе с директрисами изображён
на рис. 7.
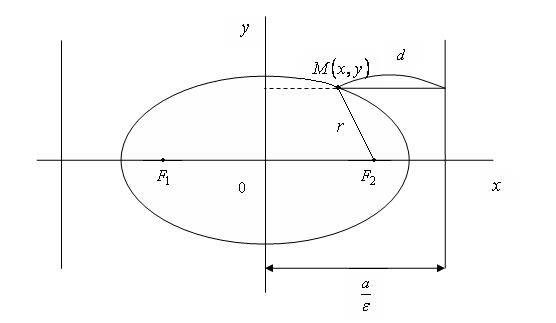
Рис. 7
Рассмотрим какую–нибудь гиперболу и введём декартову прямоугольную систему координат так, чтобы эта гипербола определялась каноническим уравнением
.
Определение 7. Две прямые, перпендикулярные к той оси гиперболы, которая её пересекает, и расположенные симметрично относительно центра на расстоянии от него, называются директрисами гиперболы.
Уравнение директрис в выбранной системе координат имеют вид
и .
Первую из них мы условимся называть левой, вторую – правой.
Так как для гиперболы
,
то
.
Отсюда следует, что правая директриса
расположена между центром и правой
вершиной гиперболы; аналогично, левая
директриса расположена между центром
и левой вершиной. Гипербола вместе с
директрисами изображена на рис. 8.
Рис. 8.
Значение директрис эллипса и гиперболы выявляется следующими двумя теоремами.
Теорема 1.
Если
– расстояние от произвольной точки
эллипса до какого–нибудь фокуса,
– расстояние от той же точки до
соответствующей этому фокусу директрисы,
то отношение
есть постоянная величина, равная
эксцентриситету эллипса:
.
Доказательство:
Предположим для определённости, что
речь идёт о правом фокусе и правой
директрисе. Пусть
– произвольная точка эллипса (см. рис.
7). Расстояние от
до правой директрисы выражается
равенством
,
а расстояние от до правого фокуса даётся второй из формул (7):
.
Отсюда имеем:
.
Теорема доказана. ■
Теорема 2. Если – расстояние от произвольной точки гиперболы до какого–нибудь фокуса, – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение есть постоянная величина, равная эксцентриситету гиперболы:
.
Доказательство: Предположим для определённости, что речь идёт о правом фокусе и правой директрисе. Пусть – произвольная точка гиперболы (см. рис. 8). Нам придётся рассмотреть два случая:
Точка находится на правой половине гиперболы. Тогда расстояние от до правой директрисы выражается равенством
,
а расстояние от до правого фокуса даётся второй из формул (10):
.
Отсюда имеем:
.
Точка находится на левой половине гиперболы. Тогда расстояние от до правой директрисы выражается равенством
,
а расстояние от до правого фокуса даётся второй из формул (15):
.
Отсюда имеем:
.
Теорема доказана. ■
Свойство эллипса и гиперболы, выраженное предыдущими теоремами, можно положить в основу определения этих линий. Именно
Определение 8. Геометрическое место точек, для которых расстояние от некоторой фиксированной точки (фокуса) и расстояние до некоторой фиксированной прямой (директрисы) находятся в постоянном отношении
,
(18)
есть эллипс, если
,
гипербола, если
,
парабола, если
.
5°. Полярное уравнение эллипса, гиперболы и параболы.
Воспользуемся определением 8 для вывода полярного уравнения эллипса, гиперболы и параболы (по форме записи общее для этих трёх линий) при некотором специальном расположении полярной оси. Отметим, что в случае гиперболы это уравнение определяет линию не целиком, а только одну её ветвь.
Пусть нам дана какая–нибудь из названных линий (эллипс, гипербола или парабола, если данная линия гипербола, то мы будем рассматривать какую–нибудь одну её ветвь) и пусть – фокус линии, – соответствующая этому фокусу директриса (в случае гиперболы в качестве и возьмём фокус и директрису, ближайшие к рассматриваемой ветви).
Введём полярную
систему координат так, чтобы полюс
совместился с фокусом
,
а полярная ось была перпендикулярно к
директрисе и направлена от неё к фокусу
(рис. 9). Обозначим, как обычно через
полярные координаты произвольной точки
на линии. Чтобы вывести уравнение линии,
будем исходить из соотношения (18)
,
где
– эксцентриситет линии, а
и
имеют тот же смысл, что и в пунктах
1°–3°.
Рис. 9.
Так как полюс совмещён с фокусом , то
.
(19)
Далее,
.
(20)
Пусть
– точка, расположенная на линии так,
что отрезок
перпендикулярен к полярной оси, и
– длина отрезка
(для параболы,
совпадает с её параметром).
Из (18) имеем
,
откуда
.
Но
;
следовательно,
.
Из последнего равенства и равенства (20) получаем:
.
Подставляя в (18) вместо и их выражения (19) и (20), найдём:
,
откуда,
.
(21)
Уравнение (21) является полярным уравнением эллипса, гиперболы (вернее одной ветви гиперболы) и параболы. Здесь – фокальный параметр, – эксцентриситет кривой. Уравнение (21) широко используется в небесной механике.