
- •Содержание
- •Эффективность инвестиций в основной капитал
- •Система показателей, характеризующих эффективность инвестиций в основной капитал
- •Расчетная часть
- •Оценка тесноты связи между фактором и результативным показателем на основе корреляционного анализа. Осуществление проверки значимости линейного коэффициента корреляции
- •Оценка тесноты связи
- •2.1.2. Проверка значимости
- •Рассчет доверительных границ для коэффициента корреляции
- •Определение параметров уравнения линейной регрессии.
- •Определение параметров
- •Оценка значимости уравнения линейной регрессии
- •Определение тренда для факторного признака
- •Расчет параметров уравнений
- •Выбор уравнения тренда
- •Заключение
- •Список литературы
- •Приложение 1 Приложение 2 Приложение 3
Рассчет доверительных границ для коэффициента корреляции
Вероятность события γ рассчитывается по формуле:
γ=1-α
Следовательно, γ=0,98 (98%)
Тогда, tγ=2,33 (по таблице нормального закона распределения)
Для значения r=0,96 найдем Z’ (по таблице Z-преобразований Фишера)
Z’=1,9459
По формуле

найдем интервал для Z’.
1,9459
– 2,33 ≤Z
≤ 1,9459 + 2,33
≤Z
≤ 1,9459 + 2,33
0,7809 ≤ Z ≤ 3,1109
По таблице Z-преобразований Фишера найдем границы для r
0,65 ≤ r ≤ 0,996
Вывод: с вероятностью γ=98% можно утверждать, что значение линейного коэффициента корреляции лежит в пределах от 0,65 до 0,996.
Определение параметров уравнения линейной регрессии.
Определение параметров
Для нахождения параметров линейной регрессии используем метод наименьших квадратов. Этот метод позволяет получить систему нормальных уравнений для оценки параметров a и b.

Для решения данной системы построим вспомогательную таблицу.
Таблица 2. Расчет сумм для определения параметров a и b линейной регрессии
|
№ |
|
|
|
|
|
1 |
69,5 |
934 |
4830,25 |
64913 |
|
2 |
103,1 |
1078,2 |
10629,61 |
111162,42 |
|
3 |
133,4 |
1137,1 |
17795,56 |
151689,14 |
|
4 |
133,5 |
1260,7 |
17822,25 |
168303,45 |
|
5 |
150,9 |
1425,7 |
22770,81 |
215138,13 |
|
6 |
166,1 |
1548,4 |
27589,21 |
257189,24 |
|
7 |
223,4 |
1711,3 |
49907,56 |
382304,42 |
|
сумма |
979,9 |
9095,4 |
151345,25 |
1350699,8 |
|
сред |
140 |
1299,3 |
25224,21 |
|
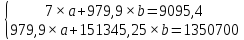
Решим эту систему при помощи матрицы.
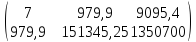
Отсюда, параметры a и b будут равны соответственно:




Решением системы уравнений являются a=534,15 и b=5,47. Следовательно, уравнение линейной регрессии будет иметь следующий вид:

Оценка значимости уравнения линейной регрессии
Для осуществления оценки существенности линейной регрессии необходимо определить коэффициент детерминации по формуле:

Для этого заполним вспомогательную таблицу:
Таблица 3. Расчет сумм для определения коэффициента детерминации
|
N |
|
|
( |
|
( |
|
1 |
914,315 |
-385,0279 |
148246,4508 |
-365,3429 |
133475,4033 |
|
2 |
1098,1070 |
-201,2359 |
40495,8702 |
-221,1429 |
48904,1633 |
|
3 |
1263,848 |
-35,4949 |
1259,8849 |
-162,2429 |
26322,7447 |
|
4 |
1264,395 |
-34,9479 |
1221,3527 |
-38,6429 |
1493,2704 |
|
5 |
1359,573 |
60,2301 |
3627,6701 |
126,3571 |
15966,1276 |
|
6 |
1442,717 |
143,3741 |
20556,1448 |
249,0571 |
62029,4604 |
|
7 |
1756,148 |
456,8051 |
208670,9385 |
411,9571 |
169708,6876 |
|
сумма |
|
|
424078,3121 |
|
457899,8571 |
|
среднее |
|
|
|
|
|
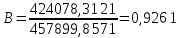
Вывод:
значение коэффициента детерминации В
близко к 1, следовательно полученное
уравнение линейной регрессии хорошо
описывает существующую зависимость
данных переменных (инвестиции в основной
капитал сельского хозяйства и продукция
сельского хозяйства). Изменение валового
выпуска продукции сельского хозяйства
на 92,6% обусловлено изменениями инвестиций
в основной капитал сельского хозяйства,
а на 7,4%
 прочих случайных факторов.
прочих случайных факторов.
Корреляционное поле и уравнение линейной регрессии представлено в Приложении 1.
Определение тренда для факторного признака
Расчет параметров уравнений
Предположим, что уравнением тренда будет являться прямая, квадратичная парабола или показательная функция.
а)
расчет параметров уравнения тренда для
линейной функции вида

Параметры
 и
и определяются методом наименьших
квадратов
определяются методом наименьших
квадратов

Таблица
4. Расчет сумм для определения параметров
 уравнения
уравнения
|
|
|
|
|
|
1 |
69,5 |
1 |
69,5 |
|
2 |
103,1 |
4 |
206,2 |
|
3 |
133,4 |
9 |
400,2 |
|
4 |
133,5 |
16 |
534 |
|
5 |
150,9 |
25 |
754,5 |
|
6 |
166,1 |
36 |
996,6 |
|
7 |
223,4 |
49 |
1563,8 |
|
сумма 28 |
979,9 |
140 |
4524,8 |




Решением
системы уравнений являются следующие
значения
 и
и .
.
Уравнение
линейного тренда имеет вид

Рассчитаем показатель рассеивания Q для линейного тренда по формуле:

Заполним вспомогательную таблицу.
Таблица 5. Расчет сумм для определения коэффициента рассеивания Q1
|
t |
|
|
|
|
|
1 |
69,5 |
75,14 |
-5,64 |
31,8096 |
|
2 |
103,1 |
96,75 |
6,35 |
40,3225 |
|
3 |
133,4 |
118,36 |
15,04 |
226,2016 |
|
4 |
133,5 |
139,97 |
-6,47 |
41,8609 |
|
5 |
150,9 |
161,58 |
-10,68 |
114,0624 |
|
6 |
166,1 |
183,19 |
-17,09 |
292,0681 |
|
7 |
223,4 |
204,80 |
18,60 |
345,96 |
|
сумма 28 |
|
|
|
1092,2851 |
Q1=1092,29
б)
расчет параметров a
и
b
для
показательной функции вида
 по формуле
по формуле

Для определения параметров a и b заполним таблицу.
Таблица
6. Расчет сумм для определения параметров
a
и b
функции

|
|
|
|
|
|
|
1 |
69,5 |
1 |
1,842 |
1,842 |
|
2 |
103,1 |
4 |
2,0133 |
4,0265 |
|
3 |
133,4 |
9 |
2,1252 |
6,3755 |
|
4 |
133,5 |
16 |
2,1255 |
8,5019 |
|
5 |
150,9 |
25 |
2,1787 |
10,8934 |
|
6 |
166,1 |
36 |
2,2204 |
13,3222 |
|
7 |
223,4 |
49 |
2,3491 |
16,4436 |
|
сумма 28 |
979,9 |
140 |
14,854 |
61,4051 |


 ;
;

Решением
системы уравнений будут следующие
значения
 и
и .
Уравнение тренда для показательной
функции будет иметь следующий вид:
.
Уравнение тренда для показательной
функции будет иметь следующий вид:

Рассчитаем показатель рассеивания Q2 для показательной функции.
Таблица 7. Расчет сумм для определения показателя рассеивания Q2
|
|
|
|
|
|
|
1 |
69,5 |
80,5704 |
-11,0704 |
122,5538 |
|
2 |
103,1 |
95,0731 |
8,0269 |
64,4316 |
|
3 |
133,4 |
112,1862 |
21,2138 |
450,0243 |
|
4 |
133,5 |
132,3797 |
1,1203 |
1,2550 |
|
5 |
150,9 |
156,2081 |
-5,3081 |
28,1759 |
|
6 |
166,1 |
184,3256 |
-18,2256 |
332,1709 |
|
7 |
223,4 |
217,5042 |
5,8958 |
34,761 |
|
сумма 28 |
979,9 |
|
|
1033,3724 |
Q2=1033,37
в)
расчет параметров a,
b
и c
для квадратичной параболы вида
 по формуле
по формуле

Заполним таблицу
Таблица
8. Расчет сумм для определения параметров
a,
b
и c
функции

|
|
|
|
|
|
|
|
|
1 |
69,5 |
1 |
1 |
1 |
69,5 |
69,5 |
|
2 |
103,1 |
4 |
8 |
16 |
206,2 |
412,4 |
|
3 |
133,4 |
9 |
27 |
81 |
400,2 |
1200,6 |
|
4 |
133,5 |
16 |
64 |
256 |
534 |
2136 |
|
5 |
150,9 |
25 |
125 |
625 |
754,5 |
3772,5 |
|
6 |
166,1 |
36 |
216 |
1296 |
996,6 |
5979,6 |
|
7 |
223,4 |
49 |
343 |
2401 |
1563,8 |
10946,6 |
|
сумма 28 |
979,9 |
140 |
784 |
4676 |
4524,8 |
24517,2 |



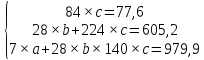

Уравнение тренда для квадратичной параболы имеет вид

Вычислим показатель рассеивания Q3
Таблица 9. Расчет сумм для определения показателя рассеивания Q3
|
|
|
|
|
|
|
1 |
69,5 |
79,76 |
-10,26 |
105,2676 |
|
2 |
103,1 |
96,77 |
6,33 |
40,0689 |
|
3 |
133,4 |
115,62 |
17,78 |
316,1284 |
|
4 |
133,5 |
136,31 |
-2,81 |
7,8961 |
|
5 |
150,9 |
158,84 |
-7,94 |
63,0436 |
|
6 |
166,1 |
183,21 |
-17,11 |
292,7521 |
|
7 |
223,4 |
209,42 |
13,98 |
195,4404 |
|
сумма 28 |
– |
– |
– |
1020,5971 |
Q3=1020,6








 )2
)2
 )2
)2








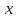



 t
t t
t t)2
t)2


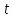






 t
t t
t t)2
t)2


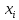







 t
t t
t t)2
t)2