4.3. Аналитическое выравнивание ряда

Суть аналитического выравнивания заключается в замене эмпирических (фактических) уровней теоретическими, которые рассчитаны по определенному уравнению. В аналитическом выравнивании наиболее часто используются следующие уравнения:

Пример выравнивания по прямой линии

Уравнение прямой выражается формулой

где - значения уровней выравненного ряда, которые нужно вычислить; , - параметры прямой;

- показатели времени.

Задачу решают методом наименьших квадратов. Для этого решают систему уравнений:

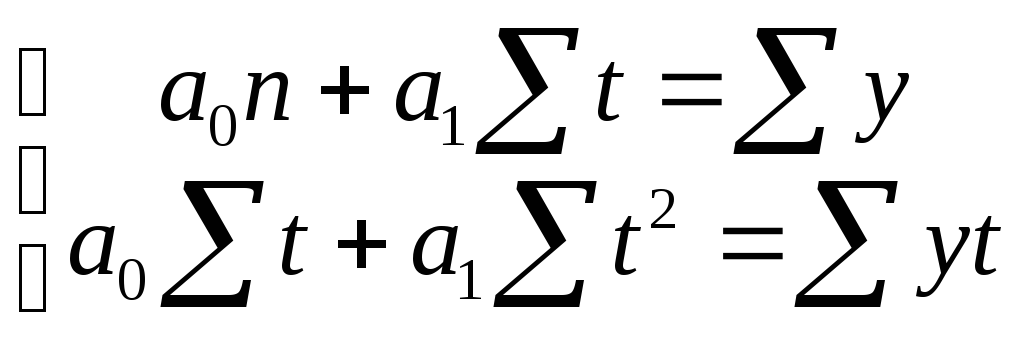
где - фактические уровни ряда динамики; - число членов ряда.

Обычно в расчетах применяется условное время.

Если вместо абсолютного времени выбрать условное время таким образом, чтобы , то записанные выражения для определения упрощаются:

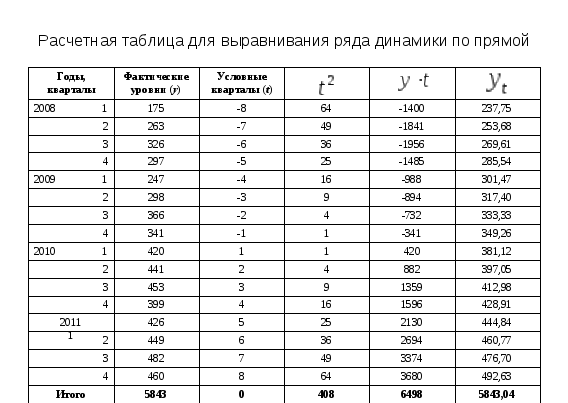
В данном случае уравнение, связывающее выручку магазина и условные кварталы:

Данное уравнение можно использовать для прогнозирования выручки магазина в будущем, подставляя в условные кварталы равные 9, 10 и т.д.

5. Измерение сезонных колебаний

Сезонными колебаниями называются более или менее устойчивые внутригодовые колебания (месячные или квартальные) в ряду динамики.

Сезонные колебания характеризуются специальными показателями, которые называются индексами сезонности.

Совокупность этих индексов образует сезонную волну.

Для вычисления индексов сезонности применяются различные методы. Мы рассмотрим метод средней арифметической.

Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней.

Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным:

где - усредненные уровни по одноименным внутригодовым периодам; - общий средний уровень.

Е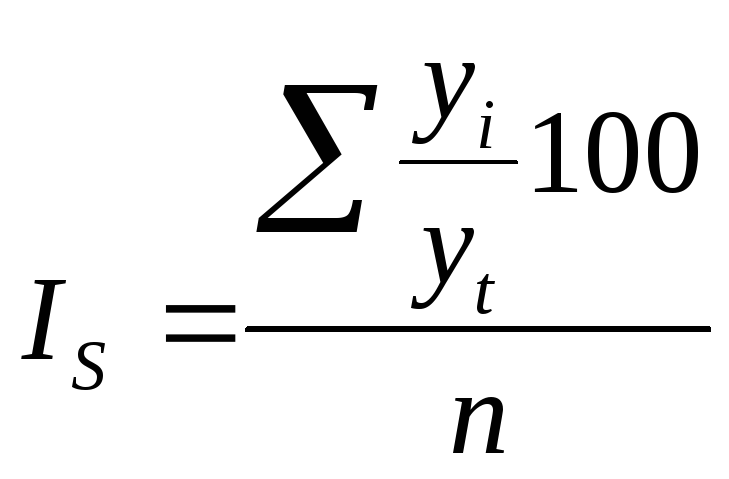сли ряд динамики содержит определенную тенденцию в развитии, то индексы сезонности определяются по формуле:

где - эмпирические уровни по одноименным внутригодовым периодам; - выравненные уровни по одноименным внутригодовым периодам; - число лет.

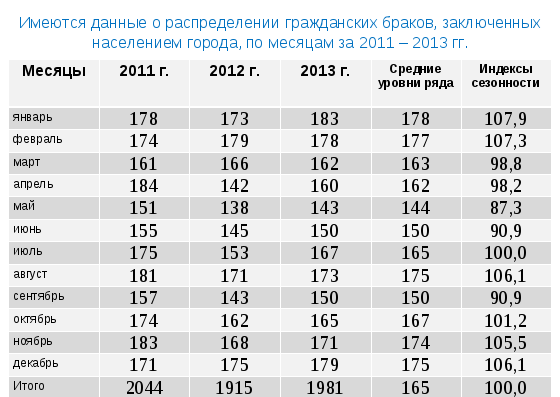
Из укрупненных данных «Итого» видно, что явление не имеет тенденцию развития. Поэтому

пользуемся формулой:

Определяем: январь: . февраль: и т.д.

Общий средний уровень:

Находим индексы сезонности: январь:

февраль: и т.д.

6. Элементы прогнозирования и интерполяции

Важное место в системе методов прогнозирования занимают статистические методы. Применение прогнозирования предполагает, что закономерности развития, действующие в прошлом (внутри ряда динамики) сохранятся и в будущем, т.е. прогноз основан на экстраполяции.

Экстраполяция, проводимая в будущее, называется перспективной и в прошлое - ретроспективной. Обычно говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию.

1. Прогнозирование по среднему абсолютному приросту.

Метод основан на предположении о равномерном изменении уровня.

где - экстраполируемый уровень;- номер уровня;- последний уровень ряда динамики;- номер последнего уровня;- срок прогноза (период упреждения);- средний абсолютный прирост.

Пример ряда с постоянным абсолютным приростом ().

t 2011 2012 2013 2014

y 100 110 120 130