МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ
образовательное учреждение
высшего образования
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
__________________________________________________________________
Кафедра вычислительной техники
Расчётно – графическая работа «Методы приближения функций»
по дисциплине: «Вычислительная математика»
Вариант: 24
Выполнил: Проверил:
Студент гр. АВТ-341, АВТФ
Калмыкова В. С. Шелудько В. И.
«14» марта 2025 г. «14» марта 2025 г.
_________________ _________________
(подпись) (подпись)
Новосибирск 2025
Оглавлени
ОПИСАНИЕ ЗАДАНИЯ 3
1. ИНТЕРПОЛЯЦИЯ ПРИ ПОМОЩИ ВСТРОЕННОЙ ФУНКЦИИ MATCHCAD LINTERP 4
2. ИНТЕРПОЛЯЦИЯ С ПОМОЩЬЮ РЕШЕНИЯ СЛАУ 5
3. ИНТЕРПОЛЯЦИЯ МЕТОДОМ ЛАГРАНЖА 9
4. ИНТЕРПОЛЯЦИЯ МЕТОДОМ НЬЮТОНА 11
5. ИНТЕРПОЛЯЦИЯ СПЛАЙНАМИ 14
6. АППРОКСИМАЦИЯ ПОЛИНОМОМ (МЕТОД НАИМЕНЬШИХ КВАДРАТОВ) 17
7. СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДОВ 20
8. ИНТЕГРИРОВАНИЕ АППРОКСИМИРУЕМОЙ ФУНКЦИИ 22
9. ВЫЧИСЛЕНИЕ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ ФУНКЦИИ В ТОЧКЕ Х0 = 2.9999 23
ЗАКЛЮЧЕНИЕ 27
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ 28
ПРИЛОЖЕНИЕ 28
ОПИСАНИЕ ЗАДАНИЯ
Для заданной дискретной функции
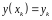
Таблица 1. Контрольное задание
|
1 |
2 |
3 |
4 |
|
0 |
1 |
2 |
3 |
|
0 |
9 |
1 |
6 |
С помощью системы MathCad, используя разные способы выполнить приближение функции методами:
1. Интерполяция с помощью решения слау.
2. Интерполяция методом Лагранжа
3. Интерполяция методом Ньютона.
4. Интерполяция сплайнами
5. Аппроксимация полиномом (МНК)
ПОРЯДОК РЕШЕНИЯ
По п.1 Записать программу MathCad приближения заданной дискретной y( xk) = yk с использованием его стандартных (встроенных) процедур. Проверить качество решения и найти значение функции при заданном значении аргумента (например, x=2.58 обеспечивающий абсолютную погрешность решения ε ≤ 0.01÷0.001 и относительную погрешность ε/y<0.01).
По п.2 Используя найденные в п.1 приближения функции, выполнить экстраполяцию на два шага вперед и оценить качество экстраполяции для каждого приближения функции.
По п.3 Для любой выбранной студентом из найденных аппроксимирующих функций вычислить значение интеграла на интервале приближения ([0;3]). Изменяя шаг интегрирования (по необходимости), найти его величину, обеспечивающую ту же погрешность, что и в п.1. Оценить значение производной при заданном значении аргумента, что и в п.1.
Интерполяция при помощи встроенной функции matchcad linterp
Зададим векторы исходных данных согласно варианту
При помощи встроенной функции Matchcad linterp(x,y,x) осуществим линейную интерполяцию и построим функцию по заданным точкам. По рисунку 1 мы можем наблюдать общий характер функции, а также участки возрастания и убывания, что позволит в дальнейшем провести анализ функции и сделать предположения о возможной аналитической формуле функции, заданной таблично.
Рисунок 1. Построение функции по заданным точкам.
При помощи встроенной функции MatchCad predict, выполним экстраполяцию на два шага вперед для построенной по заданным точкам функции.
Рисунок 2. Экстраполяция на два шага вперед для исходной функции.
В дальнейшем, оценку качества экстраполяции для различных методов интерполирования функций будем проводить на основе полученной экстраполяции для исходной функции.