
Помощник по физике
.pdf
41
значение (мкФ):
1) 0,55 и 6; 2) 4,5 и 0,6; 3 ) 0,55 и 5; 4) 0,65 и 4; 5) 0,45 и 6.
10.2 Конденсатор электроемкостью С1 = 4 мкФ был заряжен до разности потенциалов U1 = 40 В и отключен от источника тока. Если к этому конденсатору присоединить параллельно другой конденсатор электроемкостью С2 = 5 мкФ, то энергия, израсходованная на образование искры в момент присоеди-
нения второго конденсатора |
(мДж): |
|
|||
1) |
1,1; |
2) 1,2; |
3) 1,0; |
4) 1,3; |
5) 1,5. |
10.3 В однородном электрическом поле напряженности Е находится заряд q . В плоскости, перпендикулярной силовым линиям, этот заряд переместили на расстояние L. Работу, которую при этом совершили силы поля над зарядом:
1) 0; 2) EqL; 3) –EqL; 4) EL /q ; 5) нет верного.
10.4 Формула, отражающая условие потенциальности электростатического поля:
|
|
|
1 |
|
|
|
|
|
|||
1) |
E d S |
ρ dV ; |
2) Ф Е E d S ; |
3) E d l 0 ; |
|||||||
|
|||||||||||
|
S |
|
q |
|
ε0 V |
S |
|
l |
|
||
4) |
E |
|
; |
|
5) q i dV . |
|
|
|
|||
|
|
|
|
|
|||||||
|
|
|
0 |
|
i |
V |
|
|
|
||
10.5 Если плоский конденсатор с площадью пластин S = 100 см2 заполнен двумя слоями диэлектриков: фарфора толщиной d1 = 2 мм ( 1 = 5) и эбонита толщиной d2 = 1,5 мм ( 2 = 3), то его электроемкость (пФ):
1) 98,3; 2) 99,3; 3) 100,3; 4) 101,3; 5) 102,3.
10.6 Две пластины с электрическими зарядами противоположных знаков расположены на небольшом расстоянии. При уменьшении расстояния между пластинами в 2 раза, энергия электрического поля:
1) |
увеличится в 2 раза; |
2) увеличится в 4 раза; 3) уменьшится в 2 раза; |
4) |
уменьшится в 4 раза; |
5) не изменится. |
10.7 Отношение работы, совершаемой электрическим полем при перемещении положительного заряда, к значению этого заряда является:
1) потенциалом электрического поля; |
2) напряженностью электрического |
поля; 3) электрическим напряжением; |
4) электроемкостью; 5) энергией |
электрического поля. |
|

42
ПОСТОЯННЫЙ ТОК
ОСНОВНЫЕ ФОРМУЛЫ
1 Сила и плотность электрического тока:
I |
dQ |
и |
j |
I |
, |
|
|
||||||
|
||||||
|
dt |
|
S |
|||
где S – площадь поперечного сечения проводника. |
||||||
Плотность тока в проводнике: |
|
|
|
|||
j ne |
, |
|||||
где 
 - скорость упорядоченного движения зарядов в проводнике; n –
- скорость упорядоченного движения зарядов в проводнике; n –
концентрация зарядов.
2Электродвижущая сила, действующая в цепи:
A ,
q 0
где q0 – единичный положительный заряд, А – работа сторонних сил.
3 Сопротивление R однородного линейного проводника, проводимость G
проводника и удельная электрическая проводимость вещества проводника:
R ρ |
l |
; |
G |
1 |
; |
|
1 |
, |
|
S |
|
||||||||
|
|||||||||
|
|
|
R |
|
|
||||
где ρ – удельное электрическое сопротивление; S – площадь поперечного сечения проводника; l – его длина.
4 Сопротивление проводников при последовательном и параллельном соединении:
n |
1 |
n |
1 |
|
|
R R i и |
|
, |
|||
R |
|
||||
i 1 |
i 1 |
Ri |
|||
где Ri – сопротивление i-го проводника; n – число проводников.
5 Зависимость удельного сопротивления ρ от температуры:
0 |
(1 t) , |
||||
где α – температурный коэффициент сопротивления. |
|||||
6 Закон Ома: |
|
|
|
|
|
для однородного участка цепи |
I |
U |
; |
|
|
|
|||||
|
|
|
R |
||
для неоднородного участка цепи |
I |
1 2 12 |
; |
||
|
|||||
R

43
для замкнутой цепи |
I |
|
, |
|
R r |
||||
|
где U – напряжение на участке цепи; R – сопротивление участка цепи; r –
сопротивление источника тока; ( 1- 2) – разность потенциалов на концах участка цепи; 12 – ЭДС источников тока, входящих в участок; - ЭДС всех источников тока цепи.
7Закон Ома в дифференциальной форме:
j γ E ,
|
где E – напряженность электрического поля. |
|
||
8 |
Работа тока за время t : |
|
||
|
A IUt I2 Rt |
U 2 |
t . |
|
9 |
R |
|||
|
|
|||
Мощность тока: |
|
|||
P UI I2Rt U2 t . R
10 Закон Джоуля-Ленца:
Q I2Rt IUt,
где Q – количество теплоты, выделяющееся в участке цепи за время t. 11 Закон Джоуля-Ленца в дифференциальной форме:
w j E γE 2 ,
где w – удельная тепловая мощность тока. 12 Правила Кирхгофа:
первый закон Кирхгофа – алгебраическая сумма токов, сходящихся в уз ле, равна нулю:
I k 0 ;
k
второй закон Кирхгофа – в любом замкнутом контуре алгебраическая сумма падений потенциала на отдельных участках цепи равна алгебраической сумме ЭДС, встречающихся в этом контуре:
Ii R i i . i k
11 Основные характеристики постоянного электрического тока
44
11.1 Самостоятельная проводимость газа обусловлена:
1) наличием ионов; 2) созданным в газе электрическим полем; 3) нагреванием газа; 4) наличием электронов; 5) воздействием ионизирующих излучений.
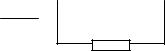
11.2 Сопротивление приведенной цепи из трех резисторов равно (R):
1) 1,5; 2) 3; 3) 0,5; 4) 2; 5) 1.
R
R 


 R
R
11.3 Средняя скорость упорядоченного движения электронов n при плотности тока j:
1) |
j |
; |
2) |
2j |
; |
3) |
n |
; 4) |
j |
; 5) нет верного. |
|
2en |
|
en |
|
ej |
en |
||||
11.4 Общее сопротивление R четырех резисторов, соединенных параллельно, равно:
1) R ОБ R ; |
2) R ОБ |
|
R |
; |
3) R ОБ 4R ; |
4) RОБ |
|
R |
; |
5) R ОБ 2R . |
|
|
|||||||||
|
||||||||||
|
|
4 |
|
|
|
2 |
|
|
||
11.5 Имеются две проволоки одинаковой длины из одинакового материала, но с разными сечениями (S1 S2). Проволоки включены последовательно.
При сравнении плотности тока j |
в проводниках: |
|||
1) j1 j2; |
2) |
j1 = j2; |
3) j1 j2; |
4) для правильного ответа данных недос- |
таточно; |
5) |
j1 и j2 |
не связаны с S1 и S2. |
|
11.6 По алюминиевому проводу течет ток I = 0,2 А. Удельное сопротивление |
||||
алюминия |
= 26 нОм·м. Если поперечное сечение провода S = 0,2 мм2, то |
|||
сила, действующая на отдельные свободные электроны со стороны электрического поля (10-21 Н):
1) 4,16; 2) 1,6; 3) 9,1; 4) 41,6; 5) 3,2.
11.7 Выражением сопротивления проводника через его размеры:
1) 1 T ; |
|
l |
|
|
E |
|
2) |
; |
3) l |
2kT |
|||
|
||||||
|
|
S |
|
|
||
|
V |
|
2 |
|
; 4) |
; |
5) q E dl.. |
||
|
||||
|
V |
1 |
||
11.8 Для существования электрического тока необходимо наличие:
1) |
проводника с малым сопротивлением; 2) свободных носителей зарядов; |
3) |
разности потенциалов и наличие свободных носителей заряда; 4) разно- |
сти потенциалов; 5) электростатического поля.
|
|
45 |
11.9 Плотность тока – это: |
|
|
1) |
величина заряда, переносимого через поверхность в единицу времени; |
|
2) |
поток заряда через поверхность; |
3) сила тока через расположенную в |
данной точке, перпендикулярную к направлению движения носителей тока
площадку, отнесенная к величине этой площадки; |
4) заряд, переносимый |
|
за 1 с через поперечное сечение проводника при силе тока в 1 А. |
||
11.10 Электрическим током называется: |
|
|
1) упорядоченное движение частиц; |
2) колебательное движение заряжен- |
|
ных частиц; 3) хаотические движения электрических зарядов; 4) направ-
ленное движение электрических зарядов; |
5) тепловое движение электро- |
нов и ионов. |
|
11.11 Электрическое сопротивление металлов и полупроводников при понижении температуры:
1) увеличивается у металлов и полупроводников; 2) уменьшается у металлов и полупроводников; 3) увеличивается у металлов, уменьшается у полупроводников; 4) уменьшается у металлов, увеличивается у полупроводников; 5) не изменяется ни у металлов, ни у полупроводников.
12 Закон Ома для участка цепи. Закон Ома для полной цепи. Работа и мощность тока
12.1 В цепь, состоящую из источника ЭДС с внутренним сопротивлением 1 Ом и сопротивления 20 Ом, включается вольтметр: первый раз – параллельно сопротивлению; второй – последовательно с ним. Показания вольтметра остаются одинаковыми. Сопротивление вольтметра (Ом):
1) 21; 2) 400; 3) 151; 4) 40; 5) нет верного.
12.2 Сила тока в проводнике с сопротивлением 10 Ом за время 50 с равномерно возрастает от 5 А до 10 А. Количество теплоты выделившееся за это время в проводнике (кДж):
1) 19; 2) 29; 3) 39; 4) 49; 5) 9.
12.3 Нагреватель электрического чайника имеет две секции. При включении одной из них вода в чайнике закипит через время t1 = 15 мин, при включении
другой – через время t2 |
= 30 мин. Если обе секции включить последователь- |
||||||||
но, то вода в чайнике закипит за время t |
(мин): |
|
|||||||
1) |
45; |
2) |
44; |
3) |
43; |
4) |
42; |
5) |
46. |
12.4 Вольтметр, включенный в сеть последовательно с сопротивлением R1, показал напряжение U1 = 198 В, а при включении последовательно с сопро-

46
тивлением R2 = 2R1 показал U2 = 180 В. Если сопротивление вольтметра Rv =
900 Ом, то напряжение в сети |
(В): |
|
|
|
|||||
1) |
216; |
2) |
218; |
3) |
215; |
4) |
220; |
5) |
217. |
12.5 Плотность тока в никелиновом проводнике длиной 4 м и удельным со-
противлением |
|
= 420 нОм·м равна |
1 МА/м2. Разность потенциалов на кон- |
||||||||||
цах проводника (В): |
|
|
|
|
|
|
|
|
|||||
1) |
1,68; |
|
2) |
0,168; |
3) |
168; |
4) |
0,0168; |
5) |
0,68. |
|||
12.6 Удельное сопротивление материала |
2 мкОм м. Плотность тока, текуще- |
||||||||||||
го по резистору длиной |
5 м, если на концах его поддерживается разность |
||||||||||||
потенциалов 2 В (МА/м2): |
|
|
|
|
|
|
|||||||
1) |
1; |
2) |
0,5; |
3) |
0,2; |
4) |
0,1; |
|
5) |
2. |
|
|
|
12.7 ЭДС батареи, если известно, что при увеличении сопротивления нагрузки, подключенной к батарее, в 2 раза напряжение на нагрузке увеличивается от 10 В до 12 В (В):
1) |
22; 2) |
15; |
3) |
17,5; |
4) 11; |
5) нет верного. |
|
|
|
|||||||
12.8 |
Закон Ома для неоднородного участка цепи записывается: |
|
||||||||||||||
1) |
I R |
2 |
ε |
|
; 2) |
I R ε ; |
3) j σE ; 4) |
Iρ |
E |
l |
E |
* ; |
||||
|
|
|||||||||||||||
|
|
1 |
|
12 |
|
|
|
S |
|
l |
||||||
|
|
|
|
E l E*l dl . |
|
|
|
|
|
|||||||
5) |
I |
|
ρ dl |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
l |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12.9 Электрический заряд, прошедший в течение 20 с через поперечное сечение провода с сопротивлением R = 3 Ом при равномерном нарастании напряжения на концах провода от U1 = 2 В до U2 = 4 В (Кл):
1) 27; 2) 400; 3) 20; 4) 13; 5) нет верного.
12.10 Если сила тока в проводнике сопротивлением R =20 Ом равномерно нарастает в течение времени t = 2 с от I0 = 0 до I = 6 А, то количество теплоты Q, выделившееся в этом проводнике за вторую секунду (Дж):
1) 420; 2) 419; 3) 418; 4) 421; 5) 422.
12.11 Электрическая плитка мощностью 1 кВт с нихромовой спиралью предназначена для включения в сеть с напряжением 220 В. Удельное сопротивление нихрома при 00С 0 = 1 мк Ом·м, а температурный коэффициент сопротивления = 0,4·10-3 К-1. Если температура спирали 9000 С, то длина проволоки диаметром 0,5 мм (м):
1) 7; 2) 8; 3) 9; 4) 10; 5) 6.
47
12.12 Если при внешнем сопротивлении R1 = 50 Ом ток в цепи I1 = 0,2 А, а при сопротивлении R2 = 110 Ом – I2 = 0,1 А, то ток короткого замыкания ис-
точника ЭДС (А): |
|
|
|
|
1) 2,4; |
2) 1,2; |
3) 2,5; |
4) 1,8; |
5) 2,2. |
12.13 Два |
последовательно |
соединенных |
элемента с одинаковыми ЭДС |
|
1 = 2 = 2В и внутренними сопротивлениями r1 = 1 Ом и r2 = 1,5 Ом замкнуты на внешнее сопротивление R. Если внешнее сопротивление R = 0,5 Ом, то разность потенциалов на зажимах каждого элемента U (В):
1) 0; 0,66; 2) 0,66; 2; 3) 2; 2,66; 4) 1; 1,66; 5) 0,66; 0.
12.14 Если источник тока с ЭДС и внутренним сопротивлением r при силе тока во внешней цепи I1 = 4 А развивает мощность Р1 = 10 Вт, а при силе тока
I2 = 2 А мощность Р2 = 8 Вт, то ЭДС источника |
(В): |
||||||||
1) |
5,5; |
2) |
11,0; |
3) |
12,0; |
4) |
10,5; |
5) |
6,5. |
12.15 Электронагревательный прибор подключен к источнику тока с ЭДС и внутренним сопротивлением r. Сопротивление R прибора при котором полезная мощность максимальна и соответствующее значение КПД:
1) |
r = R, 100%; 2) r = R, 50%; |
3) R , 50%; |
4) R , 100%; |
5) |
R 0, 100%. |
|
|
12.16 В медном проводе сечением |
6 мм2, длиной 5 м и удельным сопротив- |
||
лением = 17 нОм м течет ток. За 1 мин в проводнике выделяется 18 Дж теплоты. Плотность электрического тока (МА/м2):
1) |
770; |
2) |
77; |
3) |
7,7; |
4) |
0,77. |
|
12.17 К ЭДС относится утверждение: |
|
|||||||
1) |
работа, совершаемая сторонними силами; |
2) работа, совершаемая элек- |
||||||
тростатическими силами; 3) работа, совершаемая сторонними и электростатическими силами при перемещении единичного положительного заряда по замкнутой цепи; 4) работа сторонних сил по перемещению единичного положительного заряда; 5) разность потенциалов на внешнем участке цепи.
12.18 Закон Джоуля-Ленца в дифференциальной форме записывается:
1) |
R I 2 t ; 2) I n t ; |
3) j E E * ; |
4) j2 ; 5) |
I 1 2 12 I . |
||||||||||||
12.19 Укажите неверное уравнение Кирхгофа: |
|
|
|
|
|
R2 |
||||||||||
1) |
I3 I1 I4 0 ; |
2) |
I1R1 I1R 2 I4R 4 0 ; |
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
R4 |
|
|
|
|||||||
3) |
I1R1 I1R2 I3R3 ε; |
4) I1 I4 I3 0; |
R1 |
|
|
|
|
|
|
|
R3 |
|||||
|
|
|
|
|
|
|
|
|
||||||||
5) |
I1 const . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
A |
|
I3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
48
ЭЛЕКТРОМАГНЕТИЗМ
ОСНОВНЫЕ ФОРМУЛЫ
1 Механический момент, действующий на контур с током, помещенный в однородное магнитное поле:
|
|
|
|
, |
|
M |
pm B |
||
|
|
|
|
|
|
|
|
|
|
где B - магнитная индукция, |
pm - магнитный момент контура с током: |
|||
p m IS n ,
где S – площадь контура с током; n - единичный вектор нормали к поверхности контура.
|
|
|
2 Связь магнитной индукции B и напряженности |
H магнитного поля: |
|
|
|
|
B 0 H, |
|
|
где 0 - магнитная постоянная; - магнитная проницаемость.
3 Закон Био-Савара-Лапласа:
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
I |
d l |
, r |
|
||
d B |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
, |
|
4 |
|
|
|
r 3 |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
где d B - магнитная индукция поля, |
создаваемая элементом длины d l |
||||||||
|
|
|
|
|
|
|
|
|
|
проводника с током I ; r - радиус-вектор, проведенный от d l к точке, в которой определяется магнитная индукция.
Модуль вектора d B : |
|
|
|
||
d B |
0 |
|
Idl sin |
, |
|
4 |
r 2 |
||||
|
|
|
|||
где - угол между векторами d l и r .
4Принцип суперпозиции (наложения) магнитных полей:
B Bi ,
i

49
|
|
где B -магнитная индукция результирующего поля; B i - магнитные индукции складываемых полей.
5 Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:
B 0 2I , 4 r
где r – расстояние от оси проводника.
Магнитная индукция в центре кругового проводника с током:
B 0 |
|
I |
|
|
, |
||
2R |
|||||||
|
|
|
|
||||
где R – радиус кривизны проводника. |
|
|
|
||||
6 Закон Ампера: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
d F I |
|
|
|
||||
d l , B , |
|
||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
где d F - сила, действующая на элемент длины d l проводника с током I ,
помещенный в магнитное поле с индукцией B . 7 Модуль силы Ампера:
d F IBdl sin ,
где α – угол между векторами d l и B.
8 Сила взаимодействия двух прямых бесконечных прямолинейных параллельных проводников с токами I1 и I2 :
dF 0 2I1I2 dl , 4 R
где R – расстояние между проводниками; dl – отрезок проводника. 9 Сила Лоренца:
F q υ B ,
где F – сила, действующая на заряд q, движущийся в магнитном поле со
скоростью υ . 10 Формула Лоренца:
FQ E Q υ B ,

50
где F – результирующая сила, действующая на движущийся заряд Q,
если на него действует электрическое поле напряженностью E и маг-
нитное поле индукцией B .
11 Закон полного тока для магнитного поля в вакууме (теорема о циркуляции
|
|
|
|
n |
|
вектора |
B d l Bl dl ?0 Ik , |
||||
B ): |
|||||
|
|
L |
L |
k 1 |
|
где 0 – магнитная постоянная; |
|
|
|||
B – вектор элементарной длины конту- |
|||||
ра, направленной вдоль обхода контура; |
Bl = B cos - составляющая |
||||
вектора |
|
|
|
|
|
B в направлении касательной контура L произвольной формы |
|||||
(с учетом выбранного направления обхода); - угол между векторами B
n
и l ; Ik - алгебраическая сумма токов, охватываемых контуром.
k 1
12 Магнитная индукция поля внутри соленоида (в вакууме), имеющего N
витков: |
B |
0 N I |
, |
|
|||
|
|
l |
|
где l – длина соленоида.
13 Магнитная индукция поля внутри тороида ( в вакууме):
dФB B d S BndS,
где d S dS n – вектор, модуль которого равен dS, а направление сов-
|
|
падает с нормалью n к площадке; Вn – проекция вектора |
B на нправ- |
ление нормали к площадке. |
|
14 Поток вектора магнитной индукции через произвольную поверхность S:
ФВ Bd S BndS
S S
15 Потокосцепление (полный магнитный поток, сцепленный со всеми витками соленоида):
Ф 0 N2I S, l
где - магнитная проницаемость среды.
