2.1.3. Площадь в полярных координатах

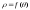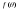Пусть в полярной системе координат дана кривая, уравнение которой ,где - непрерывная функция при 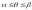. Требуется вычислить площадь криволинейного сектора, ограниченного радиусами – векторами ОА и ОВ (для которых соответственно

)

.

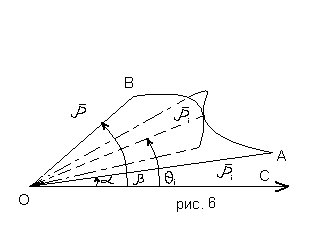
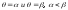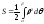Если плоская фигура ограничена несколькими кривыми, уравнения которых заданы в полярных координатах, то вычисления площади такой фигуры стараются свести к вычислению алгебраической суммы площадей криволинейных секторов.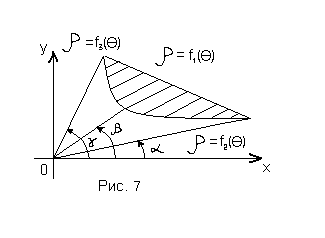

Следовательно, будем иметь

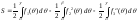.(т.е. из площади криволинейного сектора, ограниченного 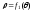, отнимаем площади криволинейных секторов, ограниченных линиями , )

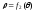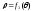2.2. Вычисление объемов тел

2. 2. 1.Вычисление объема тела по площади поперечногo сечения

Пусть дано тело произвольной формы, заключенное между плоскостями x=a и x=b. Кроме того, пусть известна площадь любого поперечного сечения (т.е. площадь сечения, образованного плоскостью перпендикулярной к оси ОХ - тела). Требуется вычислить объем этого тела.

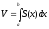, где S – площадь поперечного сечения.

2.2.2. Объем тела вращения

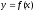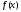Пусть вокруг оси ОХ вращается криволинейная трапеция, ограниченная осью ОX, прямыми x=a и x=b и кривой , где- непрерывная, неотрицательная на отрезке [a; b] функция. Тогда эта криволинейная трапеция опишет тело, являющееся телом вращения.

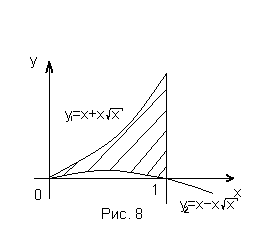
Пример 8. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной двумя ветвями кривой и прямой х=1.

Решение:

искомый объем получается как разность двух объемов, получающихся при вращении вокруг оси ОХ двух криволинейных трапеций, ограниченных сверху соответственно кривыми 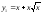и. Область определения функции

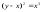
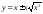
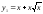
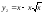
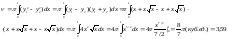
2.3. Вычисление длины дуги

2.3.1. Длина дуги в полярных координатах

Пусть на плоскости XOYдана кривая, уравнение которойy=f(x), гдеf(x) – непрерывная на отрезке [a, b] функция.

Пусть производная этой функции также непрерывная функция на отрезке [a,b].

.

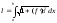Пример 9. Вычислить длину дуги кривой 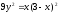между точками пересечения ее с осью ОХ.

Решение:

у=0, ,.

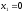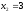Т.к. у в четной степени, то кривая симметрична относительно оси ОХ.

ОДЗ:.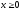

,

:

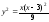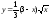
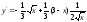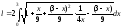
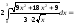
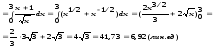
2.3.2. Длина дуги кривой, заданной параметрическими уравнениями ,,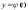 где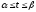

Пусть функции ,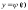- непрерывные нафункции, с непрерывными производными;,.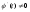

.

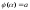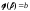Пример 10. Вычислим длину траектории

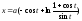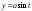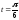,отдо.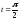

Решение:

;

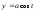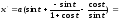
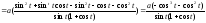
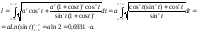
2.3.3. Длина дуги в полярных координатах

Пусть в полярной системе координат дана кривая, уравнение которой , где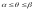. Функция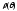имеет непрерывную производную на сегменте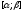

.

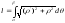Пример 11. Найти всю длину кривой .

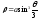Решение:

.

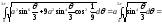
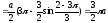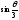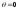Здесь имеем прии при.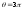

2.4. Площадь поверхности вращения

Требуется вычислить площадь поверхности, образованной вращением кривой y=f(x), гдеf(x) – непрерывная нафункция, вокруг оси ОХ.Пусть функцияf(x) имеет непрерывную производную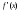на отрезке.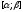

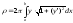Если дуга АВ задана параметрическими уравнениями, то

.

Пример 12. Определить площадь поверхности, образованной вращением вокруг оси ОХ дуги кривой 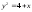, отсеченной прямой х=2.

Решение: ,:

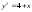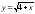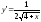
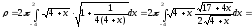
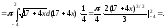
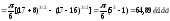
2.5. Вычисление работы переменной силы

Пусть тело движется под действием некоторой переменной силы Fпо прямой, причем направление силы совпадает с направлением движения, а работа А, произведенная силойFпри перемещении тела из т.х=а по прямой ОХ в точку х=bтой же прямой, может быть выражена (в случае когдаF=F(x) есть непрерывная функции на [a;b]) с помощью определенного интеграла следующим образом:

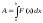. (1)

Пример 13. Рессора прогибается под нагрузкой 1,5 т на 1 см. Какую работу надо затратить для деформации рессора на 3 см? (Сила деформации пропорциональна величине деформации).

Решение: обозначим через х – величину деформации, т.к. F=kx, гдеk- коэффициент пропорциональности (коэффициент жесткости).

Известно, что при х=0,01 м F=1,500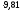(Н),

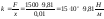то , следовательно,.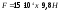

По формуле (1) работа .
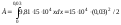