1.5. Интегрирование в симметричных пределах четных и нечетных функций

При вычислении определенных интегралов от четных и нечетных функций полезно иметь в виду следующие формулы:

(в предположении, что f(x) – непрерывная на симметричном относительно начала координат отрезке [-a;a] функция).

Пример 5. Вычислить:.

Решение:подынтегральная функция чётная, поэтому

.

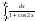
1.6. Интеграл от периодической функции по периоду

Пусть фуккция f(x) – непрерывная, периодическая с периодом Т, т.е. f(x+T)=f(x).

Для такой функции имеет место следующее свойство: интеграл от периодической функции по периоду не зависит от положения интервала интегрирования: 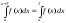,(т.е. на любом промежутке длины Т интеграл от периодической функции имеет одно и то же значение).Пример Пример 6. Вычислить: .

Решение: подынтегральная функция имеет период T=π, поэтому из верхнего и нижнего периодов можно вычесть 2π, полученный интеграл будет равен данному:

2. Приложение определенного интеграла

2.1. Геометрические приложения определенного интеграла

Вычисление площади Фигур

2.1.I.Площадь в прямоугольных декартовых координатах Площадь криволинейной трапеции

При постановке задачи определенного интегрирования мы уже рассмотрели вопрос о вычислении площади криволинейной трапеции, т.е. фигуры, ограниченной прямыми x=a, x=b, y=0 и кривой y=f(x), гдеf(x) - неотрицательная, непрерывная на отрезке [a;b] функция , и установили, что площадь указанной фигуры вычисляется по формуле(рис. 1)

Если криволинейная трапеция ограничена .осью ОХ и другой кривой y= f(x), где f(x) - непрерывная, неотрицательная на данном отрезке функция, то для вычисления площади такой фигуры надо предварительно найти абсциссы точек пересечения кривой с осью OX, затем применить формулу (I) (рис. 2).

Если плоская фигура ограничена и снизу и сверху кривыми, уравнения которых y=f₁(x) и y=f₂(x), где a≤x≤b и функции f₁(x), f₂(x) – непрерывны причём f₁(x)≤ f₂(x), искомая площадь будет представлять собой разность площадей криволинейных трапеций aABb и aCDb: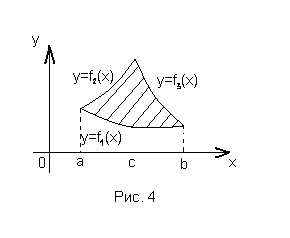

или(рис. 3).

Пусть фигура ограничена сверху или

снизу дугами нескольких кривых. Для вычисления площади такой фигуры стараются разбить эту фигуру на части прямыми, параллельными оси Оу, так , чтобы каждая часть была ограничена только одной кривой, как сверху, так и снизу.

( для случая, указанного на рис. 4).

Если непрерывная на [a;b] функция f(x) меняет на нем знак так, что некоторые части графика данной функции находятся с одной стороны от оси ОХ, а иные - с другой, то для вычисления площади фигуры поступим следующим образом: в отдельности вычисляют площадь фигуры, расположенной выше оси ОХ, и фигуры ниже оси ОХ.

А затем берут сумму абсолютных величин всех полученных интегралов.

.

Пример 7. Вычислить площадь фигуры, ограниченной осью ОХ и синусоидой при 0≤х≤2π .

2.1.2. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме

Пусть кривая, ограничивающая криволинейную трапецию сверху, задана уравнениями в параметрической форме: