- •I. Понятие определенного интеграла
- •1. 1. Основные свойства определённого интеграла
- •1. 2. Формула Ньютона-Лейбница
- •1.3. Интегрирование по частям в определенном интеграле
- •1.4. Замена переменной в определенном интеграле
- •1.5. Интегрирование в симметричных пределах четных и нечетных функций
- •2. Приложение определенного интеграла
- •2.1. Геометрические приложения определенного интеграла
- •2.1.2. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме
- •2.1.3. Площадь в полярных координатах
- •2.2. Вычисление объемов тел
- •2. 2. 1.Вычисление объема тела по площади поперечногo сечения
- •2.2.2. Объем тела вращения
- •2.3. Вычисление длины дуги
- •2.6. Вычисление центра тяжести плоской линии
- •2.7. Центр тяжести плоской фигуры
I. Понятие определенного интеграла
Пусть на [a;b] задана непрерывная функция у =f(x).
Разобьем
отрезок [a;
b]
на n
частичных отрезков с помощью
произвольно выбранных на нем точек
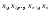 .
.
На каждом из отрезков (частичных) возьмем произвольные точки ξi (i=1,2,3…n). Во взятых точках вычислим значения функции f(x): f(ξ1), f(ξ2), f(ξ3)…, f(ξn).
Составим произведения длин ∆x1 , ∆x2, …,∆xn частичных отрезков на значения функции f(ξi).
Все эти произведения сложим и выразим сумму их через
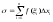 (1)
(1)
где σ=f(ξ1)∆х1+f(ξ2) ∆х2+f(ξ3)∆х3+…+ f(ξn)∆хn; или
Сумму такого вида называют интегральной суммой, составленной для функции f(x) на отрезке [a;b].
Будем неограниченно увеличивать число делений отрезка [a;b] однако так, чтобы длина ∆xi каждого отрезка [xi-1;x] стремилась к нулю; и рассмотрим получающееся при этом множество интегральных сумм σ.
Если при этом разбиении интегральные суммы будут стремиться к одному и тому же пределу, то этот предел называют определенным интегралом от функции f(x) на отрезке[a;b].
Определение.
Если
существует предел
суммы
(1) при ∆хi→0,
то
говорят, что функция f(x)
интегрируема на [a;b],
число
I
называют определенным интегралом от
функции f(x)
на [a;b].
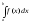 ,
,
где числа «а» и «b» называются пределами интегрирования (или интеграла), соответственно нижним, верхним; отрезок [a;b] – промежутком интегрирования.
1. 1. Основные свойства определённого интеграла
1. По определению
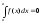 .
.
2. По определению
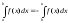 .
.
3. Каковы бы ни были числа a,b,c, всегда имеет место равенство
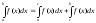 .
.
4. Постоянный множитель можно выносить за знак определённого интеграла, т. е.
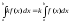 .
.
5. Определённый интеграл от алгебраической суммы функции равен алгебраической сумме их интегралов, т. е.
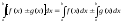 .
.
1. 2. Формула Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке [a;b] и F(x) есть какая-либо первообразная для f(x) на этом отрезке, то справедлива следующая формула:
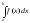 =F(b)-F(a)
. (2)
=F(b)-F(a)
. (2)
Пример 1. Вычислить:
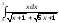 .
.
Решение: применим формулу Ньютона-Лейбница:
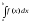 =F(x)|
=F(x)| =F(b)
-F(a)
=F(b)
-F(a)
Преобразуем подынтегральную функцию
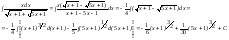 .
.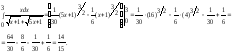
1.3. Интегрирование по частям в определенном интеграле
Пусть функции U(x) и V(x) имеют непрерывные производные на [a;b], тогда справедлива формула
 . (3)
. (3)
Пример 2. Вычислить:
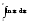 .
.
Решение: пусть
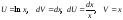 ,
т. к. функции
,
т. к. функции и
и непрерывны на
непрерывны на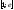 вместе со своими производными, то
согласно формуле (I) находим
вместе со своими производными, то
согласно формуле (I) находим
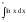
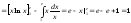 .
.
1.4. Замена переменной в определенном интеграле
Пусть
требуется вычислить
 ,
где
f(x)
-
непрерывная на [a;b]
функция. Часто
здесь бывает удобно применить, как и в
случае вычисления неопределенного
интеграла, замену переменной путем
введения вместо
старой переменной новой переменной t,
связанной
со старой
соотношением
,
где
f(x)
-
непрерывная на [a;b]
функция. Часто
здесь бывает удобно применить, как и в
случае вычисления неопределенного
интеграла, замену переменной путем
введения вместо
старой переменной новой переменной t,
связанной
со старой
соотношением
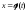 .
.
Итак,
введем новую переменную t
,
положив
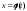 .
.
Пусть выполняются следующие условия:
а) функция
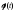 определена
и непрерывна на отрезке
определена
и непрерывна на отрезке
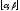 ;
;
б) при
изменении t
на
 значения функции
значения функции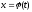 не выходят
за пределы отрезка
не выходят
за пределы отрезка
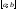 .
При этом
.
При этом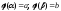 ;
;
в) Функция
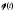 на отрезке
на отрезке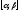 имеет непрерывную производную
имеет непрерывную производную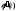 .
.
Тогда имеет место равенство
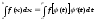 (4)
(4)
При
пользовании формулой (4) следует функцию
 стараться
выбирать
так, чтобы новый интеграл был более
простым для вычисления,
чем первоначальный.
стараться
выбирать
так, чтобы новый интеграл был более
простым для вычисления,
чем первоначальный.
Пример
3. Вычислить:
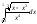
Решение: применим
подстановку:
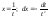 .Найдем пределы
интегралов для новой переменной при
.Найдем пределы
интегралов для новой переменной при
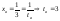 ,
при
,
при .
.
Следовательно, при применении x от 1/3 до 1 новая переменная t изменяется от 3 до 1.
Функция
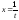 -
убывает
и непрерывна вместе
со своей производной
-
убывает
и непрерывна вместе
со своей производной
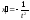 на отрезке
на отрезке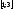
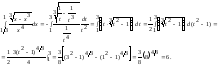
Пример
4. Вычислить:
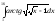 .
.
Решение.