Задание n 1 Тема: Свободные и вынужденные колебания

Начало формы

Конец формы

Маятник совершает вынужденные колебания со слабым коэффициентом затухания , которые подчиняются дифференциальному уравнению Амплитуда колебаний будет максимальна, если частоту вынуждающей силы уменьшить в _____ раз(-а).

5

Решение: Дифференциальное уравнение вынужденных колебаний имеет вид , где коэффициент затухания, собственная круговая частота колебаний; амплитудное значение вынуждающей силы, деленное на массу; частота вынуждающей силы. При слабом затухании (коэффициент затухания значительно меньше собственной частоты колебаний маятника) амплитуда колебаний будет максимальна, если частота вынуждающей силы совпадет с собственной частотой колебаний маятника (явление резонанса). Собственная частота колебаний равна: , частота вынуждающей силы . Следовательно, частоту вынуждающей силы необходимо уменьшить в 5 раз.

Задание n 2 Тема: Сложение гармонических колебаний

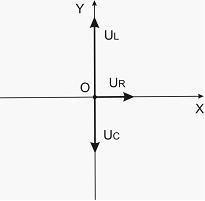Сопротивление, катушка индуктивности и конденсатор соединены последовательно и включены в цепь переменного тока, изменяющегося по закону(А). На рисунке схематически представлена фазовая диаграмма падений напряжения на указанных элементах. Амплитудные значения напряжений соответственно равны: на сопротивлении ; на катушке индуктивности ; на конденсаторе  Установите соответствие между сопротивлением и его численным значением. 1. Полное сопротивление 2. Активное сопротивление 3. Реактивное сопротивление

1
2
3

Решение: Для решения используется метод векторных диаграмм. Длина вектора равна амплитудному значению напряжения, а угол, который вектор составляет с осью ОХ, равен разности фаз колебаний напряжения на соответствующем элементе и силы тока в цепи. Амплитудное значение полного напряжения равно . Величина Полное сопротивление цепи связано с амплитудными значениями тока и напряжения законом Ома: . Амплитудное значение силы тока, как это следует из закона его изменения, равно . Тогда 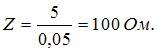Активное сопротивление Полное сопротивление цепи равно: , где реактивное сопротивление; индуктивное и емкостное сопротивления соответственно. Отсюда 

Задание n 3 Тема: Средняя энергия молекул

Кинетическая энергия (в Дж) всех молекул в 2 г неона при температуре 300 К равна …

Решение: Средняя кинетическая энергия одной молекулы равна , где – постоянная Больцмана, – термодинамическая температура, – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы . Молекула неона имеет 3 поступательные степени свободы, следовательно, . В 2 г неона содержится молекул, где масса газа, молярная масса неона, число Авогадро. Кинетическая энергия всех молекул будет равна: 

ЗАДАНИЕ N 4  Тема: Первое начало термодинамики. Работа при изопроцессах

При адиабатическом расширении 2 молями одноатомного газа совершена работа, равная 2493 Дж. При этом изменение температуры составило _____ K.

100

Решение: При адиабатическом расширении работа газа находится по формуле: ; следовательно, 

ЗАДАНИЕ N 5  Тема: Второе начало термодинамики. Энтропия

Если количество теплоты, получаемое рабочим телом от нагревателя, увеличится в 2 раза, то коэффициент полезного действия тепловой машины …

			увеличится на
			увеличится на
			уменьшится на
			уменьшится на

ЗАДАНИЕ N 6  Тема: Распределения Максвелла и Больцмана

На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала. Для этой функции неверными являются утверждения, что …

			при понижении температуры величина максимума функции уменьшается
			при понижении температуры площадь под кривой уменьшается
			с ростом температуры наиболее вероятная скорость молекул увеличивается
			положение максимума кривой зависит не только от температуры, но и от природы газа

Решение: Полная вероятность равна:, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости , при которой функция максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.

ЗАДАНИЕ N 7  Тема: Уравнения Максвелла

Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …

			0.

Решение: Из уравнения следует, что источником вихревого магнитного поля являются токи проводимости и переменное электрическое поле, для которого .

ЗАДАНИЕ N 8  Тема: Магнитостатика

На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с противоположно направленными токами, причем . Индукциямагнитного поля равна нулю на участке …

			а
			b
			c
			d

Решение: Линии магнитной индукции прямолинейных длинных проводников с токами и представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта совпадает с направлением тока в проводнике. Индукция результирующего магнитного поля определяется по принципу суперпозиции и равна нулю, если векторы и противоположно направлены и равны по модулю. Это может быть только в точках интервалов а и d. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле , то модули векторов и равны, если , так как по условию . Следовательно, индукциярезультирующего магнитного поля равна нулю в некоторой точке интервала а.

ЗАДАНИЕ N 9  Тема: Законы постоянного тока

На рисунке представлены результаты экспериментального исследования зависимости силы тока в цепи от значения сопротивления R, подключенного к источнику постоянного тока. КПД источника (в процентах) при сопротивлении Омсоставляет …

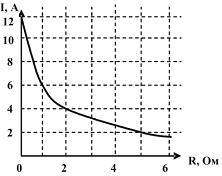
			80
			83
			75
			67

ЗАДАНИЕ N 10  Тема: Электростатическое поле в вакууме

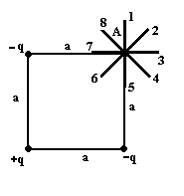Электростатическое поле создано системой точечных зарядов , и . Градиент потенциала поля в точке А ориентирован в направлении …

2

Решение: Градиент потенциала в некоторой точке связан с напряженностью поля в этой точке соотношением , поэтому для нахождения в вершине квадрата необходимо найти напряженность поля в этой точке. Согласно принципу суперпозиции полей напряженность в точке А равна: , где и – напряженности полей, создаваемых точечными зарядами , и в рассматриваемой точке соответственно. На рисунке показаны направления этих векторов. Величина напряженности поля точечного заряда определяется по формул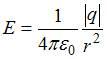е , где электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине, а заряд удален от рассматриваемой точки на расстояние , то , а . Модуль вектора равен диагонали квадрата, построенного на векторах и , то есть . Таким образом, модуль напряженности результирующего поля в точке А , а сам вектор ориентирован в направлении 6. Тогда вектор ориентирован в направлении 2.

ЗАДАНИЕ N 11  Тема: Электрические и магнитные свойства вещества

На рисунке приведена петля гистерезиса. Здесь B – магнитная индукция поля в веществе, H – напряженность внешнего магнитного поля. Коэрцитивной силе на графике соответствует отрезок …

			ОМ
			ОС
			АМ
			ОN

ЗАДАНИЕ N 12  Тема: Явление электромагнитной индукции

Проводящий плоский контур площадью 75 см² расположен в магнитном поле перпендикулярно линиям магнитной индукции. Если магнитная индукция изменяется по закону мТл, то ЭДС индукции, возникающая в контуре в момент времени (в мВ), равна …

			0,18
			180
			1,8
			18

Решение: В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: . Поскольку плоскость контура перпендикулярна линиям магнитной индукции, где S – площадь контура. Таким образом,