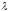Оценим значение
Практически
формула непригодна для вычисления.
Найдем np=200
0.01=2, меньше 10 Можно использовать
формулу Пуассона при X
=
2 и m=3;
сразу получаем Р3,200 =0.1805; б)
-
не более 3 деталей вышло из строя
Для
вычисления каждого слагаемого используем
формулу Пуассона, определяя значения
вероятностей по таблице при
и
приm=0,1,
2,3.
Р200(
)
= 0.8572;
в){т > 2}- не менее двух деталей вышло из строя .Здесь следует перейти к противоположному событию m<2. Тогда Р200(m>2)=1-Р0,2ОО –P1,200=0.5940.
г)2<
m
<1
от двух до четырех деталей включительно
за время t
вышли из строя следует найти Р200(2<m<
4)=Р2,200+Р3,200+Р4,200. Используя, формулу
Пуассона опять при
=2
и
m=2,3,4
по таблице находим
Р200
Задача 6.5.10
Вероятность изделию быть, бракованным равна 0.05. Найти вероятность того, что среди 1000 изделий а) 40 бракованных; б) число бракованных находится в промежутке от 40 до 70 включительно; в) сколько изделий надо взять, чтобы с вероятностью, не менее 0,9 среди них оказалось не менее 50 бракованных?
Решение: Испытание изделий на брак удовлетворяет модели испытаний Бернулли Вероятность для каждого изделия быть бракованным, р=0.05, а набракованным q=0.95. Испытаниям подвергаются n=1000 изделий.
a)
m=40;
Р 40,1000 находим по формуле Муавра
Лапласа. Определим необходимые величины:
np=50;
npq=47,5,
f(-1.45)=f(1.45)=0.1392.Окончательно
получаем
б)
Р1000 (40< m
< 70) находим по интегральной формуле
Муавра –Лапласа при
в) необходимо найти число n,удовлетворяющее условию
(Очевидно,
что
).Следовательно
Ф(x2)=1.
Получаем
По
таблице, что Ф(t)=-0,8
при t=-1,29.
Поэтому
и
после упрощения получаем
Решив
это неравенство, найдем
Следует взять менее 1198 изделий.
Функция распределения случайной величины. Непрерывная случайная величина
Функция распределения F(x) примет значение
F(x)=P(X<x). (6.5.4)
Свойства
функции распределения: F(-
)
=0;
F(+
)
= 1. О <F(x)
< 1;
если х2
>
,
to
F(
)
F(
).
Вероятность попадания случайной величины X в промежуток [а;b) определяется формулой
P(a<X<b) = F(b)-F{a). (6.5.5)
Существуют случайные величины, множество значений которых непрерывно заполняют некоторый числовой промежуток.
Если функция F(x) распределения случайной величины X непрерывна и имеет почти всюду (кроме, возможно, конечного числа точек) непрерывную производную, то случайную величину X называют непрерывной, а функцию f(x) = F'(x) называют плотностью вероятности случайной величины X. Имеют место формулы:
а)
б)
в)
;
г)
.
Вероятность того, что непрерывная случайная величина имеет конкретное значение, равна нулю.
Математическим ожиданием непрерывной случайной величины X называется число M(X), равное
(6.5.6)
Дисперсия D(x) непрерывной случайной величины
X определяется по формуле
(6.5.7)
Задача 6.5.11
Прибор
состоит из двух блоков, вероятность
безотказной работы каждого из которых
в течение времени
равна 0,5. Найти рядраспределения
для числа блоков, работающих, и момент
t=T
. Найти
функцию распределения F(x)
ДСВ
X
Решение.
Обозначим
состояние каждого блока через (R)
или
(О),
в
зависимости
от того, работает он или отказал.
Вероятность F(R)=P(O)=1/2.
Множество всех
исходов опыта Е
содержит
4 элемента, вероятность каждого равна
¼,
Е = {(0,0); (0,R);
(R,0);
(R,R)}-
Случайная
величина X-
число
работающих блоков к моменту t.
Случаю
(О
О) соответствует
значение X=0
(оба
блока отказали),
=
Р(Х
=
0) = 1/4,
случаям (О
R)
и
(R
О) соответствует
значение Х=1
(один
блок отказал),
=Р(X
=
1)=1/4+1/4=1/2. Случаю
(R
R)
соответствует
значение
Х=2
(оба
блока работают) ,
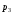=Р(Х
=
2) =1/4.Ряд
распределения для случайной величины
Х-
числа
работающих блоков имеет
вид
|
|
0 |
1 |
2 |
|
|
1/4 |
1/2 |
1/4 |
Если
x
0,
то F(x)=0,
так
как нет ни одного значения X
левее
нуля.
Если
0 < x
1
,то в промежуток (-
;0) попадает одно значениеХ=0,
следовательно,
F(x)=P(x=0)=1/4.
Если
1 < x
2,то
в промежуток (-
;х) попадает два значенияX
=0
и X=1,
следовательно,
F(x)
= Р(Х = 0)
+ Р(Х
= 1)
= ¾.
Если
2 < x
,то в промежуток (-
;x)
попадают
все значения X,
т.е.
Х=0,
Х=1, Х=2.
Следовательно,
F(x)=1.
Получаем
Задача 6.5.12
Составить функцию распределения случайной величины, распределенной по биномиальному закону.
Решение.
X
принимает
значение
с
вероятностями.
При
.
При
нужно
найти сумму значений, попавших в
промежуток от -
доx,
т.е. значения 0,1,2…k.
Следовательно,
.
Приx>n,
F(x)=1.
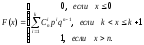
Задача 6.5.13
Случайная
величина Х
имеет плотность распределения,
пропорциональную х
при
0
и равную 0 при
и
.
а) Найти выражение для f(x)
б)
Найти М(х),
D(x),
.
Решение. а) Выражение плотности распределения имеет вид
Пользуясь свойством плотности распределения, находим
откуда
1/2
б)
Математическое ожидание М(Х)=
Дисперсия
D(X)=
Задача 6.5.14
Задана функция распределения случайной величины X:
Найти вероятность того, что случайная величина Х примет значение в интервале (1;3).
Решение. Вероятность попадания случайной величины в интервал (1;3) по формуле (1.2) равна P(1<X<3)=F(3)-F(1)=1-1/2=1/2.
Закон больших чисел. Предельные теоремы
Теорема Чебышева 6.5.1 Если Х – неотрицательная случайная величина и М(Х) – её математическое ожидание, то для любой А>0 имеет место неравенство
,
(6.5.8)
или
. (6.5.9)
Если
случайная величина имеет дисперсию
D(X),
то для любого
имеет место неравенство Чебышева:
,
(6.5.10)
или
. (6.5.11)
Если
- средняя арифметическая независимых
случайных величин
,k=1,
… n,
каждая из которых имеет
и
,
то неравенство Чебышева принимает вид
.
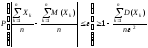(6.5.12)
Для
случайных величин, одинаково распределённых
с
и
,
неравенство (6.5.12) принимает вид
.
(6.5.13)
Если
дисперсия независимых случайных величин
равномерно ограничены числом С, то
следствием (6.5.11) является неравенство
.
(6.5.14)
Следствием (6.5.11) является также неравенство Чебышева для случайной величины, распределенной по биноминальному закону:
,
(6.5.15)
и для случайной величины, равной частности появлений события в n независимых испытаниях:
.
(6.5.16)
Теорема
Ляпунова 6.5.2
Пусть
дана последовательность независимых
случайных величин
,k=1,
… n,…,
для каждой из которых существует
математическое ожидание
=
,
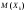дисперсия
=
и третий центральный абсолютный момент
.
Если выполняется условие
(6.5.17)
то
случайная величина
распределена нормально с математическим
ожиданиемМ(Х)=∑
и дисперсией
=
.
Теорема
Ляпунова относится к группе теорем,
объединённых общим названием центральная
предельная теорема. Одна
из простых формулировок центральной
предельной теоремы относится к одинаково
распределённым случайным величинам:
если
-
независимые одинаково распределённые
случайные величины с математическими
ожиданиями
и дисперсиями
,
то при неограниченном увеличении их
числаn
закон распределения их суммы X
приближается к нормальному с параметрами
M(X)=na
и D(X)=
.
Теорема
Лапласа 6.5.3. Пусть m
– частота появлений события A
в n
независимых испытаниях, а p
– вероятность наступления события A
в отдельном испытании. При
случайная величина
распределена нормально сМ(Х)=0
и D(X)=1,
то
есть
.
Приближение
формулы Муавра – Лапласа следует из
того, что закон распределения случайной
величины
при большомn
близок
к нормальному с плотностью вероятности
.
Задача 6.5.15
Математическое ожидание скорости ветра на аэродроме равно 7 м/с. Оценить вероятность того, что скорость ветра на аэродроме а) не превзойдет 28 м/с : б) будет не менее 35 м/с.
Решение. Случайная величина Х – скорость ветра. а) по условию А – 28 м/с. Применяем неравенство (6.5.12’):
б) По условию А = 35 м/с. Применяем неравенство (6.5.12):
.
Задача 6.5.16
Средний вес детали равен 50 г, а дисперсия равна 0,1. Оценить вероятность того, что вес случайно выбранной из партии детали окажется в границах (49,5;50,5).
Решение. Случайная величина Х – вес детали. По условию
=50
г,
=0,1
и
=0,5.
Неравенство 49,5<X<50,5
равносильно -0,5<X-50<0,5
, или
.
Поэтому применяем неравенство Чебышева
(1.7.2’):
Искомая вероятность не меньше 0,6.
Задача 6.5.17
Сумма всех вкладов в некоторую сберегательную кассу составляет 20000 руб., а вероятность того, что случайно взятый вклад не превышает 100 руб., равна 0,8. Что можно сказать о числе вкладчиков данной сберкассы?
Решение.
Пусть
Х
–
размер случайно взятого вклада ,а n
– число всех вкладов. Тогда из условия
задачи средний размер вклада
Так как
и по неравенству (1.7.1’)
то
Отсюда
и, следовательно,
Задача 6.5.18
Ёмкость
изготовляемого заводом конденсатора
должна быть по техническим условиям
равной 2 мкФ с разрешённым допуском 0,1
мкФ. Завод добился средней ёмкости,
равной 2 мкФ с дисперсией, равной 0,004
мкФ
.
Какова вероятность изготовления
бракованного конденсатора? Расчёт
провести по неравенству Чебышева,
предположив, что ёмкости конденсаторов
распределены по нормальному закону с
теми же параметрами.
Решение.
Конденсатор
будет бракованным, если отклонение
ёмкости конденсатора Х
от среднего значения М(Х)=2
мкФ будет по абсолютной величине болеем
=0,1
мкФ. По неравенству Чебышева (6.5.13 ) имеем
а
поэтому вероятность события P
Если же предположить, что значения ёмкости распределены по нормальному закону, то
Видим, что, используя значение о нормальном законе распределения, ответ получаем более точным. Неравенство же Чебышева дает грубую оценку, зато оно применимо к случайным величинам, распределенным по любому закону.
Системы случайных величин
Систему двух случайных величин (X,Y) можно изобразить случайно точкой на плоскости.
Событие,
состоящее в попадании случайной точки
(X;Y)
в область D,
принято обозначать в виде
(X;Y)
D.
Закон распределения системы непрерывных случайных величин (X,Y) будем задавать с помощью функции плотности вероятности f(x,y).
Вероятность попадания случайной точки (X,Y) в область D определяется равенством
Функция плотности вероятности обладает следующими свойствами:
Если все случайные точки (X;Y) принадлежат конечной области D , то последнее условие принимает вид
.
(6.5.18)
Математическое ожидание дискретных случайных величин X и Y, входящих в систему, определяются по формулам
(6.5.19)
а математические ожидания непрерывных случайных величии - по формулам
(6.5.20)
(6.5.21)
Точка
(
;
)
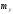называетсяцентром
рассеивания системы
случайных величин (X,Y).
Математические
ожидания
и
ту
можно
найти и проще, если случайные величины
X
и
Y
независимы.
В этом случае из законов распределения
этих случайных величин можно определить
математические ожидания
и
ту
по
формуле
(6.5.22)
(6.5.23)
Дисперсии дискретных случайных величин X и Y определяются по формулам
;
(6.5.24)
.
(6.5.25)
Дисперсии же непрерывных случайных величин X и Y, входящих в систему, находятся по формулам
;
(6.5.26)
.
(6.5.27)
Средние квадратичные отклонения случайных величин X и Y определяются по формулам
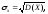
(6.5.28)
Для вычисления дисперсий могут быть применены формулы
(6.5.29)
Важную роль в теории систем случайных величин играет так называемый корреляционный момент (ковариация)
(6.5.30)
Для дискретных случайных величин корреляционный момент находится по формуле
(6.5.31)
а для непрерывных – по формуле
(6.5.32)
Корреляционный момент можно также найти по формуле
(6.5.33)
Здесь
для дискретных величин X и Y и
(6.5.34)
для непрерывных величин.
Случайные величины X и Y называются независимыми, если вероятность одной из них принимает значение, лежащее в любом промежутке области ее значений, и не зависит от того, какое значение приняла другая величина. В этом случае
M(XY)=M(X)M(Y);
Для характеристики связи между величинами X и Y рассматривается так называемый коэффициент корреляции
(6.5.35)
являющийся безразмерной величиной.
Если
случайные величины X
и
Y
независимы,
то
=0.
Если же случайные
величины
X
и
Y
связаны
точной линейной зависимостью Y=aX+b,
то
=
sgna
,т.е.
=1
при а > 0 и
=
-1 при а < 0. Вообще же коэффициент
корреляцииудовлетворяет
условию
-1
1.
Задача 6.5.19
Дана таблица 6.5.1, определяющая закон распределения системы двух случайных величин (X,Y):
|
X y |
20 |
40 |
60 |
|
10 |
3 |
|
0 |
|
20 |
2 |
4 |
2 |
|
30 |
|
2 |
5 |
Таблица 6.5.1
Найти:
1) коэффициент
;
2) математическое ожидание
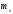и
;3)
дисперсии
и
;
4) коэффициент корреляции
.
Решение.
Таблица 6.5.2
|
X Y |
20 |
40 |
60 |
∑ |
|
10 |
3 |
|
0 |
4 |
|
20 |
2 |
4 |
2 |
8 |
|
30 |
|
2 |
5 |
8 |
|
∑ |
6 |
7 |
7 |
∑20 |
=1|
X y |
20 |
40 |
60 |
|
|
10 |
3 |
|
0 |
4 |
|
20 |
2 |
4 |
2 |
8 |
|
30 |
|
2 |
5 |
8 |
|
|
6 |
7 |
7 |
|
20
=1
Таблица 6.5.3
|
|
-21 |
-1 |
19 |
|
-12 |
3 |
|
0 |
|
-2 |
2 |
4 |
2 |
|
8 |
|
2 |
5 |
Найдём
из условий (6.5.1):
Вычислим дисперсии по формулам:
или
,
или
,
Вычислим
и
и составим таблицу 1.8.3
Определим ковариацию по формуле
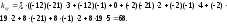
Вычислим
коэффициент корреляции:
