Системы дифференциальных уравнений

Определение6.4.3.Нормальной системой дифференциальных уравнений называется система вида

(6.4.42)

Здесь число уравнений равно числу неизвестных функций.

Решением системы (6.4.42) называется совокупность n функций 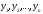, удовлетворяющих всем уравнениям системы.

Частным решением системы (6.4.42.) называется решение, удовлетворяющее начальным условиям:

при x=x₀,

где x₀,- заданные числа.

Семейство решений системы (6.4.42), зависящее от n произвольных независимых постоянных :

называют обычно общим решением этой системы.

6.5.Теория вероятности

Основные формулы и теоремы.

Классическое определение вероятности

Вероятность события А обозначается символом р или р(А). При классическом определении вероятность события А равна

(6.5.1)

Отношению числа случаев m , благоприятствующих ему из общего числа n равновозможных, единственно возможных и несовместных случаев, к числу n , т.е.очевидно, что число 0P (А) 1.

Задача 6.5.1.

По телевидению передано 10 снимков, из них три снимка с искажениями. Какова вероятность, что два взятых на удачу снимка: а) не имеют искажений б) оба имеют искажения? в) один имеет искажение?

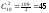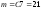Решение: Два снимка из десяти можно выбрать n=способами (порядок не важен). Обозначим события: а) Событие А- обаснимка не .имеют искажения т.е. они выбраны из 7 качественных снимков. Это можно сделать способами. Следовательно,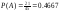.б) Событие В - оба снимка имёю искажения, т.е. они взяты .из трех некачественных . Получим, откуда. в) СобытиеС - один имеет искажение и один не имеет искажение, т.е. один снимок взят из 3 , а 1 - из 7. По правилу произведения это можно сделать способами, поэтому

Задача 6.5.2

а)Сколько различных трехзначных чисел можно записать при помощи цифр 1; 2? б)Найти вероятность, что записано число 121. (Событие А).

Решение: а) Трехзначные числа - упорядоченные тройки элементов, образованные из цифр 1 и 2, размещения с повторениями из двух элементов по 3. Их число б) Событию А благоприятствует один исходm=1. Поэтому .

Теоремы сложения и умножения вероятностей

Непосредственный подсчет вероятности, основанный на построении полной группы событий, практически редко может быть осуществлен. Поэтому основной задачей теории является рассмотрение различных теорем, с помощью которых вероятности одних событий определяются по вероятностям других событий. Важнейшие из них - теоремы сложения и умножения. Условная вероятность события А относительно события В равна:

(6.5.1)

Выражение (6.5.1) получило название теоремы умножения вероятностей.

В случае произведения более чем двух событий теорема умножения вероятностей принимает вид

Событиянезависимы всовокупности, если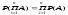 (6.5.2)

Теорема сложения вероятностей: если событияпопарно несовместимы, то вероятность суммы событий равна сумме вероятностей этих событий:

(6.5.3.)

Если несовместные события образуют полную группу, то сумма вероятностей этих событий равна 1. В частности, для двух, противоположных событий Аи имеет место равенство

, и поэтому вероятность противоположного события вычисляется по формуле

Если события совместны, то формулы для вероятности суммы этих событий усложняются. Например, вероятность суммы двух местных событий равна

_,

а вероятность суммы трех совместных событий

Задача 6.5.3.

Из коробки, содержащей 5 красных и 3 черных шариковых ручки, извлекают 2 ручки. Найти вероятность того, что: а) обе ручки красные. 6) ручки разных цветов. Рассмотреть 2 случая: 1) извлеченная первой ручка не возвращается в коробку; 2) извлеченная первой ручка возвращается в коробку перед извлечением второй.

Решение. Введём обозначения для событий: А - обе ручки красного цвета; В - ручки разных цветов. Следует определить Р(А) и Р(В)

Введём события, связанные с извлечением одной ручки: А1-первая ручка: красная; - первая ручка чёрная, А2 - вторая ручка красная; вторая ручка черная. Тогда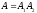и.

Применяем формулы (6.5.1) и (6.5.3).

В данном случае события и несовместны.

1 случай. 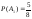Так как после наступления ручка не возвращается, то в коробке окажется 7 ручек. Из которых 4 красных и поэтому

2 случай. 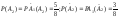(так как после наступления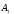ручка возвращена в коробку).

а) 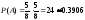. б).Задача 6.5.4

Прибор собирается последовательно четырьмя рабочими. Независимо от остальных 1-й может допустить брак вероятностью 0,1,2-й и 3-й - с вероятностью 0,09, а 4-й -0,15. Готовый прибор относится к I сорту, если ни один рабочий не допустил брак, ко II, если брак допущен 2-м или 3-м рабочим, к III сорту, если брак допустили 1 -й или 4-й рабочие и признаётся негодным в остальных случаях. Найти вероятности следующих событий: А - прибор признан I сорта; В - II сорта; С - Ш сорта; D - прибор признан негодным.

Решение: Обозначим Через Аi событие, состоящее в том, что i-ый рабочий не допустил брак, тогда -i-ый рабочий допустил брак i=1,2,3,4 . В условии дано Р(А1) =01; Р(А2)= Р(АЗ)=0,09 ; Р(А4)=0,15. Тогда P(A1)=0.9; P(A2)=P(A3)=0.91; Р(A4) = 0.85

Интересующие нас события можно представить следующим образом: A=A1А2А3А4; B=A1A2A3A4+А2А3А4;C=A1A2A3A4+A2A3А4. Событие D противоположно сумме событий А+В+С, т.е. D= A+B+C:

Применяем формулы (6.5.2) для независимых событий и (6.5.3) для несовместных событий-слагаемых в выражениях для В и С, получим

Задача 6.5.5

Вероятность того, что проходящая машина потребует заправки в данном пункте, равна 0.3. Сколько должно пройти машин чтобы с вероятностью не меньшей, чем 0.9 можно было утверждать, что хотя бы одна потребует заправки?

Решение: Введем обозначения для событий : Аi –i-я машина потребует заправки и С - хотя бы одна машина из и потребует заправка. Тогда С=А1+А2+...+Аn.

Однако все слагаемые совместны, поэтому перейден противоположному событию С -“ни одна машина из n потребует заправки” получим

События A1 ,А2,..., An , а следовательно , _ A1 А2…Аn независимы и имеют одну и ту же вероятность

Поэтому По условию задачи 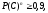те. Решая это неравенство, найдем последовательно 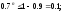n lg 0.7lg 0,1, откуда . Окончательно получаемn=7.

Формула полной вероятности. Формула Бейеса

Из теорем сложения и умножения получается формула полной вероятности и формула Бейеса. Если события A1, A2,...,An образуют полную группу (гипотезы) и событие А, то может произойти вместе с одним из событий А, тогда

- формула полной вероятности .

Если же в результате проведения опыта зафиксировано появление события А, то переоценка вероятности гипотез равна - формула Бейеса.

Задача 6.5.6

Известно, что в партии из 600 электрических лампочек 200 изготовлены на первом заводе, 250 на втором заводе и 150 на третьем заводе. Известны также вероятности 0.97, 0.91 и 0.93 того, что лампочка окажется стандартно о качества при изготовлении ее соответственно 1,2,3 заводами. Какова вероятность, что на удачу выбранная из данной партии лампочка окажется стандартной.

Решение: Обозначим через А событие, состоящее в том , что лампочка окажется стандартной:

А - лампочка изготовлена на 1 заводе,

А - лампочка изготовлена на 2 заводе,

А - лампочка изготовлена на 3 заводе.

Известно, что РА1(А)=0,97; РА2(А)=0,91;РА3(А)=0,93.

Событие А1,А2,А3 образуют полную группу и по формуле полной вероятности находим

Задача 6.5.7

При массовом производстве некоторого изделия вероятность того, что оно окажется стандартным, равна 0 95. Для контроля производится некоторая упрощенная проверка стандартности изделия, которая дает положительный результат в 99% случаев стандартности изделии и в 3% случаев для нестандартных изделий. Какова вероятность стандартности изделий, выдержавшего упрощенную проверку?

Решение: Введем события;

А1 - изделие окажется стандартным,

А2 - изделие окажется нестандартным.

А 3 - изделие выдержит упрощенную проверку.

События A1, А2 образуют полную группу. До проверки Р(А1)=095,Р(А2)=0 05. Известно, что РА1(А)=0,99 РА2(А)=0,03. Нас интересует вероятность стандартности издания, прошедшего проверку, т.е РА(А1). По формулам Бейеса получаем

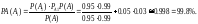
Это означает, что в среднем только 2 изделия из 1000 , успешно прошедших проверку, будут нестандартным.

Схема испытаний Бернулли (повторение опытов)

Вероятность того, что в n независимых испытаниях, в, каждом из которых вероятность появления события равна p(0<p>1), событие наступит ровно m раз (безразлично, в какой последовательности), есть

где q=1-p.Вероятность- того, что событие наступит:

а) менее m раз:

б) более m раз:

в) не более m раз:

г) не более m раз:

Вероятность наступления события А хотя бы один раз при проведении n независимых испытаний, равна:

, где

Наивероятнейшее значение 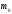числа наступления события А при проведении n независимых повторных испытаний, вычисляется по формуле

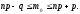
Задача 6.5.8

Вероятность того, что денежный приемник автомата при опускании одной монеты срабатывает правильно, равна 0,97. Сколько нужно опустить монет, чтобы наивероятнейшее число случаев правильной работы автомата было равно 100?

Решение. Двойное неравенство

np-q<<np+p при p=0.97, q=0,03 и даёт

Следовательно, с одной стороны,

0,97n-0.03< 100, откуда

С другой стороны

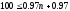откуда n302.09 т.е. 102,09.

Поэтому n= 103 , как то целое число которое заключено между 102,09 и 103.12.

Предельные теоремы

Если число испытаний n велико , то применение формулы Бернулли приводит к громоздким вычислениям . В таких случаях пользуются предельными теоремами Лапласа. а) Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которые вероятность появления события равна р(о<р < 1), событие наступит ровно m раз, выражается приближенным равенством

Функция у(х) - четная, т.е. у(-х)= γ(х). При х>5 можно считать, что γ(x)=0. б) интегральная теорема Лапласа. Вероятность того, что в n, независимых испытаниях, в каждом из которых вероятность появления. события равна р, событие наступит не менее m1 раз и не более m2 раз, выражается приближенным равенствам

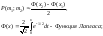
При >5 полагают Ф(х)=5. Функция Лапласа – нечетная, т.е.

Ф(-х)=-Ф(х), Ф(0)=0.

Если число испытаний достаточно велико , а р - мало при, этом 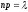не больше 10 (10), то вероятностьможно найтиприближенно по формуле Пуассона:.

Задача 6.5.9

Прибор состоят из 200 деталей, каждая из которых за врем t может выйти из строя с вероятностью р=0 01. Найти вероятность того, что за время t выйдут из строя: а) 3 детали; б) не более 3 деталей; г) от двух до четырех деталей включительно.

Решение: В данном случае n=200, m=0.01, q=0.99, m- количество

деталей ,

вышедших аз строя за время t. а) m=3;РЗ;200 по формуле Бернулли равно