Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами

Линейным однородным дифференциальным уравнением n-ого порядка с постоянными коэффициентами называется уравнение

y⁽ⁿ⁾+p₁y^(n-1)+p₂y^(n-2)+…+p_n-1y^|+p_ny=0, (6.4.29)

в котором все члены имеют первую степень относительно функции ее производных, а коэффициенты p₁,p₂,…,p_n – постоянные.

Общее решение линейного однородного уравнения (6.4.29) имеет вид

y=C₁y₁+C₂y₂+…+C_ny_n, (6.4.30)

где y₁,y₂,…y_n – линейно независимые частные решения (фундаментальная система решений) этого уравнения, а C₁,C₂,…C_n – произвольные постоянные.

Для отыскания общего решения уравнения (6.4.29) составляется характеристическое уравнение

rⁿ+p₁r^n-1+p₂r^n-2+…+p_n-1r+p_n=0, (6.4.31)

которое получается из уравнения (6.4.29) заменой в нем производных искомой функции соответствующими степенями r, причем сама функция заменяется единицей.

Тогда общее решение уравнения (6.4.29) строится в зависимости от характера корней уравнения (6.4.31):

1. каждому действительному однократному (т.е. простому) корню r в общем решении соответствует слагаемое вида Ce^rx;

2. каждому действительному корню r кратности k в общем решении соответствует слагаемое вида (C₁+C₂x+…+C_k-1x^k-1)e^rx;

3. каждой паре комплексных сопряженных однократных корней ив общем решении соответствует слагаемое вида;

4. каждой паре комплексных сопряженных корней икратностиL в общем решении соответствует слагаемое вида

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

y^||+py^|+qy=f(x) (6.4.32)

Оно отличается от соответствующего линейного однородного уравнения

y^||+py^|+qy=0 (6.4.33)

наличием в правой части некоторой функции f(x).

Для нахождения общего решения уравнения (6.4.32) сначала нужно найти общее решение уравнения (6.4.33), а затем найти какое-либо частое решениеy^* уравнения (6.4.32). Их сумма есть общее решение данного неоднородного уравнения (6.4.32):

y=+y^*.

Рассмотрим два метода нахождения частного решения.

Метод неопределенных коэффициентов.

Если правая часть уравнения (6.4.32) имеет вид

(6.4.34)

где  и  -действительные числа, а P_n(x) и Q_m(x) – многочлены соответственно n-й и m-й степени с действительными коэффициентами, то частное решение y^* уравнения (6.4.32) ищется в виде

(6.4.35)

где M_s(x) и N_s(x) – многочлены s-й степени (s – наибольшая из степеней n и m) с неопределенными буквенными коэффициентами, а k – кратность, с которой входит в число корней характеристического уравненияr²+pr+q=0, соответствующего однородному дифференциальному уравнению (6.4.33).

Для того, чтобы найти коэффициенты многочленов M_s(x) и N_s(x), искомое частное решение (6.4.35) подставляют в левую часть дифференциального уравнения (6.4.32) и производят соответствующие упрощения; затем в полученном тождестве приравнивают коэффициенты при подобных членах в левой и правой частях, что дает систему линейных уравнений относительно искомых коэффициентов, из которой определяют эти коэффициенты.

Укажем вид частного решения y^* для некоторых частных случаев функции (6.4.34):

1)если =0, =0 (т.е. =0), тоf(x)=P_n(x) и частное решение ищется в виде

y^*=x^k(A₀xⁿ+A₁x^n-1+…+A_n),

где k – кратность, с которой нуль входит в число корней характеристического уравнения;

2)если =0 (т.е. =), то и частное решение ищется в виде

y^*=x^k (A₀xⁿ+A₁x^n-1+…+A_n),

где k – кратность, с которой  входит в число корней характеристического уравнения;

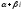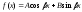3)если =0, n=m=0 (т.е. =), тои частное решение ищется в виде

где k – кратность, с которой входит в число корней характеристического уравнения.

В том случае, если правая часть уравнения (6.4.32) есть сумма функций вида (6.4.34), т.е.

f(x)=f₁(x)+f₂(x)+…+f_r(x),

нужно предварительно найти частные решения соответствующие функциямf₁(x),f₂(x),…,f_r(x). Тогда частное решение уравнения (6.4.32.) запишется в виде

(6.4.36)

Метод вариации произвольных постоянных

Более общим методом решения линейного неоднородного уравнения (6.4.32) является метод вариации произвольных постоянных.

Пусть y₁ и y₂ – линейно независимые частные решения однородного уравнения (6.4.33). Тогда общее решение неоднородного уравнения (6.4.32) следует искать в виде

y=C₁(x)y₁+C₂(x)y₂, (6.4.37)

где функции C₁(x) и C₂(x) определяются из системы уравнений

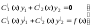(6.4.38)

Решая систему алгебраических уравнений (6.4.38), находим

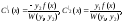(6.4.39)

где

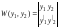(6.4.40)

- определитель Вронского, составленный для решений y₁ и y₂.

Интегрируя равенства (6.4.39), получаем

(6.4.41)

откуда, подставляя найденные функции C₁(x) и C₂(x) в соотношение (6.4.37), получим общее решение линейного неоднородного уравнения (6.4.32).