
- •Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
- •1. Цели и задачи дисциплины
- •2. Требования к уровню освоения содержания дисциплины
- •3.Трудоемкость дисциплины по видам занятий
- •4. Содержание дисциплины
- •4.1. Разделы дисциплины и виды занятий (в часах)
- •4.2. Содержание разделов
- •I семестр
- •Раздел 1. Элементы векторной алгебры и аналитической геометрии
- •Раздел 2. Введение в математический анализ: функция, теория пределов,
- •Раздел3. Дифференциальное исчисление функции одной переменной
- •Раздел 4. Функции нескольких переменных
- •II семестр Раздел 5 Элементы теории функции комплексного переменного и высшей алгебры
- •Раздел6. Неопределенный интеграл
- •Раздел7. Определенный интеграл
- •Раздел8. Кратные, криволинейные, поверхностные интегралы
- •III семестр
- •Раздел 9. Элементы теории поля
- •Раздел 10. Обыкновенные дифференциальные уравнения
- •5. Перечень практических занятий
- •I семестр
- •II семестр
- •III семестр
- •IV семестр
- •5 Самостоятельная работа студентов (срс)
- •5.3 Примерный перечень тем курсовых проектов (работ).
- •5.4 Примерный перечень тем рефератов.
- •5.5 Самостоятельное изучение тем разделов программы (материалы для самостоятельной работы студентов:умк дисциплины «Математика»).
- •6.Методические указания к самостоятельной работе студентов.
- •6.1.Векторный анализ
- •6.2.Числовые ряды Основные понятия
- •Простейшие свойства сходящихся рядов
- •Остаток ряда
- •Необходимый признак сходимости ряда
- •Положительные ряды
- •I. Признаки сравнения рядов
- •II. Признак Даламбера (в предельной форме)
- •III. Признак Коши (в предельной форме)
- •IV. Интегральный признак Коши
- •Знакопеременные ряды
- •Достаточный признак сходимости знакопеременных рядов
- •Свойства абсолютно сходящихся рядов
- •Функциональные ряды
- •Понятие функционального ряда и его области сходимости
- •Мажорируемость функционального ряда
- •Равномерная сходимость функционального ряда
- •Степенные ряды
- •Область сходимости степенного ряда
- •Нахождение интервала и радиуса сходимости ряда
- •Условия разложения функции в ряд Тейлора
- •Разложение в ряд маклорена некоторых элементарных функций
- •I Разложение функции
- •II Разложение функции
- •III Разложение функции
- •IV Разложение функции
- •V Разложение функции
- •6.3.Комплексные числа
- •Используя правило возведения в степень, получим
- •6.4.Дифференциальные уравнения Основные понятия
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах. Интегрирующий множитель
- •Уравнения Лагранжа и Клеро
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка.
- •Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Системы дифференциальных уравнений
- •6.5.Теория вероятности
- •Оценим значение
- •6.6. Математическая статистика Вариационные ряды
- •Основные формулы
- •Выборочный метод. Общие вопросы.
- •Эмпирическая функция распределения.
- •Оценка генеральной доли признака
- •Элементы проверки статических гипотез
- •Элементы корреляционного анализа Линейная корреляция
- •Основные формулы
- •Построение теоретического закона распределения по опытным данным. Статистическая гипотеза. Понятие о критериях согласия. Критерий 2 Пирсона.
- •7.Контрольные работы
- •7.1 Контрольная работа №5 Векторный анализ
- •Числовые ряды
- •Комплексные переменные
- •Дифференциальные уравнения
- •7.2Котрольная работа №6
- •7.3 Контрольная работа №7
- •7.4 Контрольная работа №8
- •Математическая статистика
- •8. Учебно-методическое обеспечение дисциплины
- •9.Карта обеспеченности студентов учебниками, учебными пособиями, учебно-методическими материалами по дисциплине "Математика".
- •10. Перечень контрольных вопросов
- •Семестр II
- •Семестр III
- •Семестр IV
III Разложение функции
Разложение
в ряд этой функции можно получить так
же, как и для

Но
можно получить его путем дифференцирования
разложения для
 :
:
 ,
,

Пример
6.2.32. Разложить функцию
 в ряд по степеням х.
в ряд по степеням х.
Решение:


IV Разложение функции
Мы должны получить разложение логарифмической функции (в ряд Маклорена) по степеням х. Надо, чтобы сама функция и все ее производные имели смысл при х=0.
Если
взять
 ,
, ,
, и
т. д.
и
т. д.
Как
видим, f(0)
и f(n)(0)
при всяком
n
лишены смысла.
Поэтому рассматриваем функцию
 Эта функция и все ее производныеопределены
при х=0.
Эта функция и все ее производныеопределены
при х=0.
Итак,
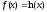 ;
;
Разложим эту функцию в ряд, используя возможность почленного интегрирования степенных рядов.
Найдем
 ;
производнаяможет
быть разложена
в ряд Маклорена, т. к. дробь
;
производнаяможет
быть разложена
в ряд Маклорена, т. к. дробь
 может рассматриваться как сумма
геометрической прогрессии (убывающей)
при
может рассматриваться как сумма
геометрической прогрессии (убывающей)
при (знаменатель прогрессииq=-x):
(знаменатель прогрессииq=-x):

где
 (радиус сходимости ряда)
(радиус сходимости ряда)
Проинтегрируем
этот степенной ряд почленно в промежутке
 , где
, где (интервал интегрирования не выходит за
пределы интервала сходимости ряда):
(интервал интегрирования не выходит за
пределы интервала сходимости ряда):
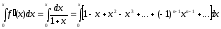
 ,
,

Сохраняется ли это равенство при х=±1
При
х=±1 теряет смысл функция
 ,
поэтому равенство при х=-1 лишено смысла.
,
поэтому равенство при х=-1 лишено смысла.
При
х=1 сохраняет смысл функция
 ,
она обращается в число
,
она обращается в число Ряд
Ряд сходится (по признаку Лейбница).
сходится (по признаку Лейбница).
Остается проверить, имеет ли место равенство:
(*)

Из
рассмотренных выше рассуждений
справедливость равенства (*) пока еще
не вытекает, т. к. доказали только, что
разложение функции
 верно при
верно при .!Для
проверки равенства (*) проведемоценку
остаточного члена при х=1:
.!Для
проверки равенства (*) проведемоценку
остаточного члена при х=1:
Закон образования производных найти легко:


Остаточный член (в форме Лагранжа):

 найдем
найдем
 при х=1:
при х=1:

Т.
к.
 ,
то при
,
то при стремится к нулю:
стремится к нулю: при
при .
А это означает (теорема 1), что ряд (*)
сходится и имеет своей суммой число
.
А это означает (теорема 1), что ряд (*)
сходится и имеет своей суммой число ,
т. е. равенство (*) верно.
,
т. е. равенство (*) верно.
Итак,
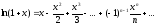 ,
,
V Разложение функции
 ;
эту дробь при
;
эту дробь при
 можно рассматривать как сумму убывающей
геометрической прогрессии со знаменателем
можно рассматривать как сумму убывающей
геометрической прогрессии со знаменателем :
:

Интегрируя
в пределах от 0 до х, где
 ,
получаем:
,
получаем: ;
откуда имеем:
;
откуда имеем:

 ,
,
 (что будет показано ниже)
(что будет показано ниже)
Проверим, не сохраняется ли это равенство и при х=±1.
При х=-1 – самостоятельно!
При
х=1: ряд принимает вид:

который сходится (по теореме Лейбница).
!Остается проверить, имеет ли место равенство:
(*)

Для этого поступим следующим образом:
 т.
е. приостанавливаемся на (n+1)
члене !!!
т.
е. приостанавливаемся на (n+1)
члене !!!
Интегрируем это равенство (конечное число слагаемых) в промежутке от 0 до 1:

т.к.
 при
при ,
то, следовательно правая часть
,
то, следовательно правая часть при
при (в силу равенства (**)):
(в силу равенства (**)): при
при ;
это и означает, что сумма ряда (*)
;
это и означает, что сумма ряда (*) ,
т. е. равенствоверно.
,
т. е. равенствоверно.
6.3.Комплексные числа
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Число
 ,
где
,
где и
и -
действительные числа, а
-
действительные числа, а -
так называемая мнимая единица, называется
-
так называемая мнимая единица, называется комплексным
числом. Действительные числа
комплексным
числом. Действительные числа и
и называются соответственно действительной
и мнимой частями комплексного числа
называются соответственно действительной
и мнимой частями комплексного числа и обозначаются:
и обозначаются: -
- есть
действительное число; если
есть
действительное число; если ,
а
,
а ,
то число
,
то число называется
числом мнимым.
называется
числом мнимым.
Два
комплексных числа и
и считаются
равными, если равны их действительные
и мнимые части, т. е.
считаются
равными, если равны их действительные
и мнимые части, т. е.
 =
=

 при
при и
и
Будем
изображать комплексное число
 с помощью точки на плоскости, абсцисса
которой равна
с помощью точки на плоскости, абсцисса
которой равна ,
а ордината
,
а ордината .
Тогда всякое комплексное число изобразится
с помощью определенной точки, так
называемой комплексной плоскости.
.
Тогда всякое комплексное число изобразится
с помощью определенной точки, так
называемой комплексной плоскости.
Положение
точки, изображающей комплексное число
z
, можно определить также с помощью
полярных координат r
и
φ
будем называть соответственно модулем
и аргументом комплексного числа z:
r
=|z|;
φ = Arg
z
.
Из определения модуля и аргумента
следует, что если
 ,
тоx
= r
cos
φ
=|z
| cos
(Arg
z);
y
=r
sinφ=|z|
sin(Arg
z);
,
тоx
= r
cos
φ
=|z
| cos
(Arg
z);
y
=r
sinφ=|z|
sin(Arg
z);

tgφ
 (при
х
(при
х ).
).
Заметим, что величина j=Arg z имеет бесчисленное множество значений, отличающихся одно от другого на целое, кратное 2p. Если величину одного из углов обозначить через j0, то совокупность величин всех углов запишется выражением
Arg z=j0+2pk (k=0,±1, ±2,…).
Значение j=Arg z, принадлежащее промежутку ]- p,p[, называется главным и обозначается j0=arg z, т.е -p<arg z£p.
Следовательно,
Arg z= Arg z++2pk (k=0,±1, ±2,…).
Зная действительную х и мнимую у части комплексного числа z и пользуясь тем, что tg (arg z)=y/x, можно вычислить arg z по формуле

Числу 0 не приписывается какое - либо значение аргумента.
Всякое комплексное число, отличное от нуля, можно представить ь в тригонометрической форме
z=x+iy=rcosj+irsinj=r(cosj+isinj).
Замечание 1.1. С помощью формулы Эйлера eij=cosj+isinj можно представить комплексное число в показательной форме :
z=reij .
Комплексные
числа z=x+iy
и
 называют взаимно-сопряженными. При этом
называют взаимно-сопряженными. При этом .
.
Сложение, вычитание и умножение комплексных чисел производят по правилам сложения, вычитания и умножения алгебраических многочленов, полагая при этом i2=-1, i3=-i, i4=1,…
При сложении и вычитании комплексных чисел отдельно складываются и вычитаются их действительные и мнимые части:
(x1+iy1)±( x2+iy2)=( x1+x2)+i(y1+y2).
Умножение:
(x1+iy1) ( x2+iy2)=(x1x2-y1y2)+i(x1y2+x2y1).
Деление определяется как действие, обратное умножению.
Деление
удобно производить следующим образом;
сначала умножить делимое и делитель на
число, сопряженное делителю, после чего
делитель станет действительным числом
 ,
а затем произвести деление действительной
и мнимой частей отдельно;
,
а затем произвести деление действительной
и мнимой частей отдельно;

Если воспользоваться тригонометрической формой записи чисел
z1=r1(cosj1+isinj1); z2=r2(cosj2+isinj2);
получим
z1 z2=r1 r2 [(cos(j1+j2)+isin(j1+j2)], (6.3.1)
т.e, при умножении комплексных чисел их модули перемножаются, а аргументы складываются:
 .
(6.3.2)
.
(6.3.2)
Из правила умножения следует правило возведения в целую положительную степень: если
z=r(cosj+isinj), то zn=rn(cosnj+isin nj). (6.3.3)
Нетрудно убедиться, что формула справедлива и при целом отрицательном n.
Извлечь
корень целой положительной степени n
из числа z
- значит найти такое число
 ,n-я
степень которого равна z.
,n-я
степень которого равна z.
