Условия разложения функции в ряд Тейлора

Вид коэффициентов ряда Тейлора указывает на то, что ставить задачу о разложении в ряд Тейлора можно лишь по отношениюк бесконечно дифференцируемой в точке х₀ функции; но это есть только необходимое условие разложения в ряд Тейлора:далеко не всякая бесконечно дифференцируемая функция может быть представлена своим рядом Тейлора.

Может оказаться, что составленный по ряд Тейлора: 1) хотя и сходится в некотором интервале. Но его сумма не совпадает с, кроме как в т. х=х₀; или 2) он даже вообще может оказаться расходящимся для хх₀.

Другими словами, остается пока открытым вопрос: 1) сходится ил ряд где-нибудь, кроме точки х=х₀ ; 2) возникает также и второй вопрос: если ряд сходится в некотором интервале, то какая функция является суммой этого ряда

Та функция , с помощью которой вычислялись коэффициенты ряда, или какая-либо другая функция (см. Увар., стр. 77; Бермант, стр. 591). Пусть функция бесконечно дифференцируема в некоторой окрестности точки х₀.

Найдем значения функции и ее производных в т. х₀ в составим для 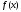ряд Тейлора.

Выясним, при каких условиях можно утверждать, что составленный ряд сходится к

Т. к. поведение ряда (сходимость или расходимость) зависит от коэффициентов ряда, а коэффициенты определяются функцией , то, очевидно, вопрос о сходимости ряда Тейлора надо изучать с помощью свойств самой функцииТ. к. функцияимеет в окрестности т. х₀ производные любых порядков, то для всех значений х из этого интервала и для любого n имеет место формула Тейлора (выводится в дифференциальном исчислении).

(6.2.10)

где – остаточный член этой формулы.

С помощью этой формулы можно дать ответ на поставленный выше вопрос.

Теорема 6.2.18. (необходимое и достаточное условие). Для того, чтобы ряд Тейлора функции сходился к ней, необходимо и достаточно, чтобы остаточный член 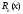формулы Тейлора для стремился к нулю при

Теорема 6.2.19.(достаточный признак). Если в некотором интервале, содержащем т. х₀, модули всех производных функции ограничены одним и тем же числом: 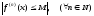, то функцияв этом интервале разлагается в ряд Тейлора.

Разложение в ряд маклорена некоторых элементарных функций

I Разложение функции

Эта функция имеет производных всех порядков при любом х: (n=1,2,3,…)

Проверим выполнение условий теоремы 2:

если взять любой промежуток , то в нем верна оценка

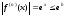
(т. е. для всех значений х модули всех производных ограничены одним и тем же числом ).

Поэтому по теореме 2 функция 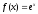разлагается в сходящийся к ней ряд Маклорена в любом промежутке, т. е. иначе говоря, при всех х (всюду).

Найдем коэффициенты ряда:

таким образом, при любых х верно разложение:

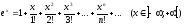
Пример 6.2.31. Разложить в ряд Маклорена функцию ; указать интервал сходимости

Решение,

II Разложение функции

Она имеет производные всех порядков:

Очевидно, условия теоремы 2 выполняются: при всех х и n производная функции по модулюне превосходит единицы.

Следовательно, разлагается в ряд Маклорена и разложение справедливо при всех х.

Найдем коэффициенты ряда:

Таким образом, при любых х верно разложение:

(*) ,

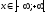
В ряде присутствуют только нечетные степени х; это естественно, т. к. 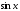- нечетная функция.

Можно считать равенство (*) определением функции , т. к. радиус сходимости ряда равен бесконечности, и, следовательно, сумма ряда определена и непрерывна на всей числовой оси. Эту сумму и можно по определению считать функциейтакое определение не связано с геометрическим построением, с которыми эта функция так тесно связана в школьном курсе математики.