Простейшие свойства сходящихся рядов

Теорема 6.2.1. Если ряд (6.2.1)сходится и имеет сумму S, то ряд (6.2.2) (где С – какая-либо постоянная) также сходится и имеет суммуcS.

Теорема 6.2.2. Если ряды 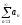(6.2.1) и(6.2.2)сходятся и имеют соответственно суммы S и , то ряды (6.2.3) и(6.2.4) также сходятся и их суммы соотвественно равныS+ и S-.

Вывод. Таким образом: 1) сходящиеся ряды можно почленно складывать и вычитать так же, как и конечные суммы; 2) можно умножать члены сходящегося ряда на одно и тоже постоянное число, в результате получаются так же сходящиеся ряды.

Пример 6.2.3. Найти сумму ряда:

По теореме 6.2.2:

Остаток ряда

Пусть дан ряд: (6.2.1). Отбросим любое фиксированное число «k» его первых членов, тогда получим новый ряд (6.2.2)

Определение 6.2.2. Ряд (6.2.2), который получается из данного ряда (6.2.1) путем отбрасывания некоторого конечного числа членов, взятых подряд начиная с первого, называется остатком данного ряда.

Если отброшено k первых членов, то остаток называется k-м остатком и его можно записать в виде суммы .

По своему поведению ряды (6.2.1) и (6.2.2) тесно связаны.

Теорема 6.2.3. Ряды (6.2.1) и (6.2.2): 1) либо одновременно сходятся 2) либо одновременно расходятся.

Вывод. Таким образом: 1) если сходится данный ряд , то сходится и любой его отстаток; 2) если сходится какой-либо остаток ряда, то сходится и сам ряд.

Следствие: Ряды (6.2.3) и(6.2.4.), у которыхлишь конечное число членов отличается друг от друга, либо одновременно сходятся, либо одновременно расходятся.

Д-но, если, например, ,начиная с nk, то ряды (6.2.3.) и (6.2.4.) сходятся или расходятся одновременно с рядом (6.2.2):

Таким образом, отбрасывание конечного числа членов ряда (или добавление к ряду конечного числа членов) не влияет на сходимость или расходимость этого ряда.

Поэтому при исследовании ряда на сходимость можно: 1) изменять конечное число членов этого ряда, а так же 2) добавлять или 3) отбрасывать конечное число членов.

Пример 6.2.4.Исследовать на сходимость ряд

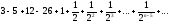(n4)

Решение. Отбросим в данном ряде 4-ре первых члена, тогда получим новый ряд:

(n=1, 2, 3, …)

который сходится как геометрическая прогрессия с 1. Следовательно, сходится и рассматриваемый ряд.

Необходимый признак сходимости ряда

Рассмотрим необходимый признак сходимости ряда, т. е. укажем условие, при невыполнении которого ряд наверняка расходится.

Теорема 6.2.4. Если ряд (6.2.1)сходится, то его общий член стремится к нулю при неограниченном возрастании номера этого члена, т. е..

Пусть ряд (6.2.1) сходится и сумма его равна S, т. е.

Наряду с этим равенством имеет место и такое равенство:

Запишем теперь очевидное равенство: , найдем предел

Таким образом, для сходимости ряда (6.2.1) необходимо, чтобы общий член его имел предел, равный нулю.

Пример 6.2.5. +

Данный ряд расходится, т. к. его общий член приимеетпредел, равны 1:

Пример 6.2.6..

Ряд расходится, т. к.=sin не существует.

Положительные ряды

Ряд, все члены которого неотрицательны, называется положительным рядом.

Рассмотрим признаки, с помощью которых удается, не прибегая к вычислению предела частичных сумм, установить, сходится ли данный положительный ряд или нет. Эти признаки, правда, не дают ответа на вопрос о том, какова сумма данного ряда (если ряд расходится).

Но отыскивание суммы сходящегося ряда – это трудная задача и ее удается решить только в отдельных, частных случаях, применяя разнообразные приемы преобразования частичных сумм или какие-либо другие методы.

Рассмотрим ряд признаков сходимости положительного ряда.