Операции над множествами
1
.Объединением
множеств А и В называется множество,
состоящее из элементов, принадлежащих
А или В.
C=А
В,
если
означает, что
или
Объединение множеств обозначается символами "+" и "∪"
Пример
А={-6, -3, 0, 3, 6}, B={0,2, 4, 6, 8}. Тогда A∪B = {-6, -3, 0, 2, 3, 4, 6, 8}.
Свойства операции объединения
A∪B = B∪A (коммутативность);
(А∪B) ∪C = А (B∪C) (ассоциативность);
Если A⊇B, то А∪В= А;
=А объединение А и
пустого множества равно А.
2
.
Пересечением множеств А и В
называется множество, состоящее из
элементов, принадлежащих А и В С=
А
В,
если
означает, что
и
Определение Если множества А и В не имеют общих элементов, их пересечение равно пустому множеству; в этом случае множества А и В называются непересекающимися А∩В=
Пересечение множеств обозначается символами "∩" и "·" (знак умножения):
С = А∩В или С = АВ.
Свойства операции пересечения множеств.
1. A∩B = B∩A (коммутативность);
2. (A∩В)∩С = А∩(В∩С) (ассоциативность);
3. Если A⊇B, то А∩B = В;
4. А∩
=
.
Законы дистрибутивности:
A∪(B∩C) = (A∪B)∩(A∪C);
A∩(B∪C) = (A∩B)∪(A∩C);.
3.Разностью множеств называется множество, состоящее из элементов, принадлежащих А, но не принадлежащих В
С
=
А\В, если
означает, что
и
Замечание
Свойства разности
1. А\ = А
2. \А=
3. А\А=
4. Множество
=(А\В)(В\А)
называется симметрической разностью
множеств А и В или кольцевой суммой
.
Обозначается (А/В)(В\А)=АВ
Свойства симметричной разности
1.
2.
=А
3.
U=
3.
Дополнение множества 
Дополнением
множества А до
( I ) будет множество, состоящее из
элементов, не принадлежащих А и
обозначается
(х
,
если х
А)
Теорема. Дополнение к объединению некоторых множеств равно пересечению их дополнений , дополнение к пересечению множеств равно объединению их дополнений
A\(B∪C) = (A\B)∩(A\C);
A\(B∩C) = (A\B)∪(A\C).
Определение Множества А и В находятся в общем положении, если
,
,
,
,
,
Лекция 2 Отношение. Способы задания отношений
Исследователя всегда интересуют различные свойства объектов: свойства, относящиеся к отдельным объектам (например, "быть женщиной", "быть белым", "иметь низкую теплопроводность") и свойства, характеризующие связи между несколькими объектами (например, свойства "быть родственниками" и "быть больше" относятся к парам объектов, свойство "находиться между" - к тройкам объектов, свойство "располагаться в вершинах квадрата" - к четверкам объектов).
Такие свойства принято называть отношениями. При этом свойства отдельных объектов называются унарными (одноместными) отношениями, свойства, относящиеся к парам объектов, - бинарными отношениями, свойства, относящиеся к наборам из n объектов, - n-арными отношениями
Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей теории баз данных. Отношения являются математическим аналогом таблиц.
Определение Отношения – один из способов задания взаимосвязей между элементами множества.
Пример отношений из школьного курса математики являются:
на множестве целых чисел Z отношения "делится", "делит", "равно", "больше", "меньше", "взаимно просты";
на множестве прямых пространства отношения "параллельны", "взаимно перпендикулярны", "скрещиваются", "пересекаются", "совпадают";
на множестве окружностей "пересекаются", "касаются".
Факт принадлежности кортежа (x, y) отношению R, часто обозначают с помощью инфиксной формы записи: xR y.
Примерами таких записей из курса математики являются: x > y, a = b, m || l.
Способы задания отношений
Отношения могут задаваться:
формулы y = x2 +5x - 6 - бинарные отношения на множестве действительных чисел;
формула x + y = любовь -бинарное отношение на множестве людей.
- матричным представлением
Определение Матрицей бинарного отношения – называется матрица
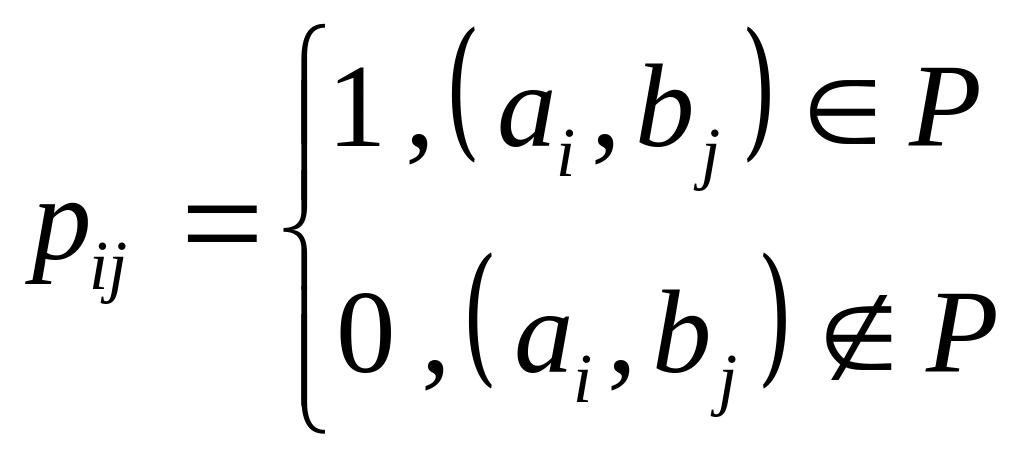
или 1 – если имеет место соотношение
и 0 если оно отсутствует.
Пример
задать
отношение
»быть
строго меньше»
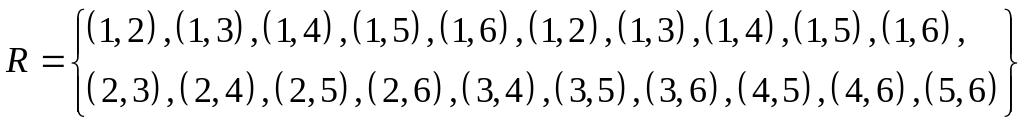
матрица бинарного отношения
графическое представление При таком представлении элементы множества X изображаются вершинами графа (точками плоскости), а элементы (x, y) отношения дугами (стрелками), соединяющими первую компоненту x отношения со второй компонентой y.