§ 4. Скорость

Скорость– это векторная величина, которая определяет как быстроту движения, так его направление в данный момент времени. Вектором средней скорости за интервал времени 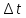называется отношение приращения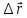радиуса – вектора точки к промежутку времени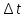

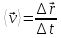. (4.1)

Направление вектора средней скорости совпадает с направлением .

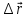Единица скорости – м/с.

Для характеристики движения очень важна мгновенная скорость, т.е. скорость в данный момент времени и в данный точке траектории. Мгновенная скорость – векторная величина, равная производной по времени от радиуса вектора 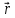, рассматриваемой точки:

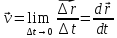. (4.2)

Вектор мгновенной скорости направлен по касательной к траектории в сторону движения.

Модуль мгновенной скорости (скалярная величина) равен первой производной по времени

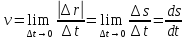. (4.3)

При неравномерном движении модуль мгновенной скорости с течением времени изменяться. Поэтому можно ввести скалярную величину 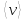среднюю скорость неравномерного движения:

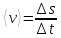. (4.4)

Длина пути s, пройденного точкой за промежуток времени от 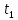до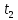задается интегралом:

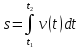. (4.5)

При прямолинейном движении точки направление вектора скорости сохраняется неизменным.

Движение точки называется равномерным, если модуль её скорости не изменяется с течением времени для него:

.

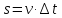Если модуль скорости увеличивается с течением времени, то движение называется ускоренным, если же он убывает с течением времени, то движение называется замедленным.

§ 5. Ускорение и его составляющие

Ускорение – векторная величина, характеризующая быстроту изменения скорости движущегося тела по величине и направлению.

   Средним ускорением точки в интервале времени Δt называется вектор 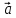, равный отношению приращения вектора скорости Δ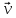к промежутку Δt.

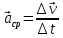. (5.1)

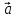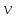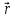   Ускорением (мгновенным ускорением) точки называется векторная величина , равная первой производной скоростипо времени (или вторая производная радиус - векторапо времени):

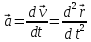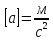, (5.2)

  Ускорение точки в момент времени 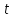равно пределу среднего ускорения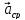при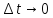

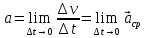
  В декартовой системе координат вектор 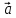можно записать через его координаты:

,

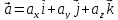где ,,.

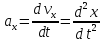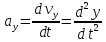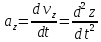Модуль вектора ускорения

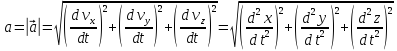
Вектор 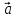 можно представить в виде суммы двух составляющих:

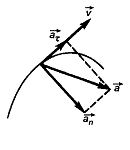
Рисунок 5.1

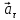- тангенциальная составляющая ускорения направлена по касательной траектории точки и равна

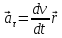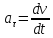; (5.3)

Тангенциальное ускорени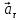е - характеризует быстроту изменения модуля вектора скорости точки (характеризует изменение скорости по величине).

Для равномерного движения: 

; ,

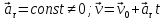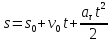где 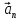- нормальная составляющая ускорения(нормальное ускорение) направлена по нормали к траектории и рассматриваемой точке в сторону к центру кривизны траектории.

Криволинейную траекторию можно представить как совокупность элементарных участков, каждый из которых может рассматриваться как дуга окружности некоторого радиуса R (называемого радиусом кривизны кривой в окружности данной точки траектории).

Рисунок 5.2

,

, ,

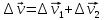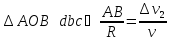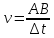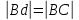
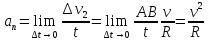
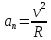. (5.4)

  Нормальное ускорение характеризует быстроту изменения направления вектора скорости (характеризует изменение скорости по направлению).

Модуль полного ускорения:

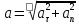. (5.5)

Классификация движений зависит от тангенциальных и нормальных составляющих:

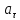=0, 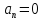- равномерное прямолинейное движение;

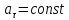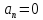, - равноускоренное движение;

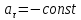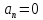, - равнозамедленное движение;

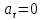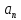, =const – равномерное движение по окружности;

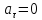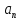, =f(t) – равномерное криволинейное движение.