
- •Глава I. Физические основы механики
- •§ 1. Введение. Предмет физики. Методы физического исследования
- •§ 2. Роль физики в развитии техники и влияние техники на развитие физики
- •§ 3. Механика и её разделы. Система отсчета. Траектория, длина пути и вектор перемещения
- •§ 4. Скорость
- •§ 5. Ускорение и его составляющие
- •§ 6. Угловая скорость и угловое ускорение
- •Глава II. Динамика материальной точки
- •§ 7. Первый закон Ньютона.Масса. Импульс
- •§ 8. Второй закон Ньютона
- •§ 9. Третий закон Ньютона
- •§ 10. Закон сохранения импульса
- •§ 11. Принцип относительности Галилея. Преобразование Галилея
- •§ 12. Силы в механике
- •§ 13. Энергия. Работа и мощность
- •§ 14. Кинетическая и потенциальная энергия механической системы
- •§ 15. Закон сохранения и превращения энергии
- •§16. Удар абсолютно упругих и неупругих тел
- •Глава III. Механика твердого тела
- •§ 17. Момент инерции
- •§ 18. Кинетическая энергия вращения
- •§ 19. Момент силы. Основное уравнение динамики вращательного движения твердого тела
- •§ 20. Момент импульса и закон его сохранения
- •Глава IV. Основы молекулярной физики
- •§ 21. Основы молекулярно-кинетической теории газов
- •§ 22. Термодинамическое состояние тела
- •§ 23. Идеальный газ
- •§ 24. Уравнение состояния идеального газа
- •§ 25. Основное уравнение молекулярно-кинетической теории идеальных газов
- •§ 26. Скорости, характеризующие состояние газа
- •§ 27. Средняя длина свободного пробега молекул
- •§ 28. Явления переноса
- •Глава V. Основы термодинамики
- •§ 29. Внутренняя энергия термодинамической системы
- •§ 30. Число степеней свободы
- •§ 31. Первое начало термодинамики
- •§ 32. Работа газа при его расширении
- •§ 33. Теплоемкость
- •§ 34. Молярная теплоемкость при постоянном объеме
- •§ 35. Молярная теплоемкость при постоянном давлении. Уравнение Майера
- •§ 36. Применение первого начала термодинамики к изопроцессам
- •§ 37. Адиабатический процесс
- •§ 38. Политропические процессы
- •§ 39. Обратимые и необратимые процессы. Круговой процесс (цикл)
- •§ 40. Кпд кругового процесса
- •§ 41. Энтропия
- •§ 42. Второе начало термодинамики
- •§ 43. Третье начало термодинамики
- •§ 44. Тепловые двигатели и холодильные двигатели
- •§ 45. Теорема Карно.Цикл Карно
- •Глава VI. Реальные газы. Жидкости. Твердые тела
- •§ 46. Уравнение Ван-дер-ваальса
- •§ 47. Изотермы реальных газов
- •§ 48. Свойства жидкостей. Поверхностное натяжение
- •§ 49. Смачивание
- •§ 50. Капиллярность
- •§ 51. Явление капиллярности в быту, природе и технике
- •§ 52. Давление под искривленной поверхностью жидкости
- •§ 53. Кристаллические и аморфные твердые тела
- •§ 54. Изменение агрегатного состояния
- •§ 55. Фазовые переходы
- •§ 56. Диаграмма состояния
§ 47. Изотермы реальных газов
Изотерма реального газа представляет собой зависимость молярного объема газа от давления при постоянной температуре.
При высоких температурах изотерма реального газа отличается от изотермы идеального газа только некоторым искажением формы.
При
некоторой температуре
 -
критической температуре – на изотерме
появляется точка перегиба К – критическая
точка. Соответствующие, этой точке
объем
-
критической температуре – на изотерме
появляется точка перегиба К – критическая
точка. Соответствующие, этой точке
объем и давление
и давление называются критическими. Изотерма при
называются критическими. Изотерма при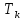 называется критической изотермой.
называется критической изотермой.

Рисунок 47.1
При уравнение Ван-дер-Ваальса соответствует
кривая 1-2-3-4-5-6-7. Однако, на участке 5-3
сжатие вещества сопровождается
уменьшением давления, следовательно в
этой области вещество распадается на
две фазы – жидкость и пар.
уравнение Ван-дер-Ваальса соответствует
кривая 1-2-3-4-5-6-7. Однако, на участке 5-3
сжатие вещества сопровождается
уменьшением давления, следовательно в
этой области вещество распадается на
две фазы – жидкость и пар.
Фаза – совокупность всех частей системы, обладающих одинаковым химическим составом и находящихся в одинаковом термодинамическом состоянии.
Истинные до критические изотермы реального газа имеют вид 1-2-6-7 и являются кривыми непрерывного перехода вещества из газообразного состояния (участок 6-7) в жидкое (участок 2-1). Участок 6-2 соответствует равновесному сосуществованию жидкости и газа.
Вещество
в газообразном состоянии при температуре
ниже критической называется паром, а
пар, находящийся в равновесии со своей
жидкостью, называется насыщенным (Ж+П).
Пар при изотермическом сжатии претерпевает
процесс сжижения. Газ, при температурах
 не может быть превращен в жидкость ни
при каком давлении.
не может быть превращен в жидкость ни
при каком давлении.
При некоторых условиях могут быть реализованы метастабильные состояния 5-6 и 2-3. Участок 2-3 изображает перегретую жидкость, 5-6 – пересыщенный пар.
§ 48. Свойства жидкостей. Поверхностное натяжение
Жидкость является агрегатным состоянием вещества, промежуточным между, газообразным и твердым. В газах нет закономерности во взаимном расположении молекул (хаотическое расположение). В твердых телах наблюдается дальний порядок – молекулы образуют кристаллическую решетку. В жидкостях дальний порядок отсутствует, а имеет место ближний порядок в расположении молекул – их упорядоченное расположение повторяется на расстояниях, сравнимых с межатомными. Тепловое движение молекулы в жидкости это ее колебание около определенного положения равновесия в течение некоторого времени, после чего молекула скачком переходит в новое положение, отстоящее от исходного на расстояние порядка межатомного.

Рисунок 48.1
Радиус
r
молекулярного действия – расстояние
(порядка
 м), при котором можно пренебречь силами
притяжения между молекулами жидкости.
Сфера радиусомr
называется сферой молекулярного
действия.
м), при котором можно пренебречь силами
притяжения между молекулами жидкости.
Сфера радиусомr
называется сферой молекулярного
действия.
Силы, действующие на молекулуА внутри объема жидкости со стороны окружающих молекул, в среднем скомпенсированы. Для молекулыВ, расположенной на поверхности, равнодействующая сил R направлена внутрь жидкости. Результирующие силы всех молекул поверхностного слоя оказывает на жидкость молекулярного (внутреннее) давление.
Молекулы
поверхностного слоя жидкости обладают
большей потенциальной энергией, чем
молекулы внутри жидкости. Эта дополнительная
энергия, называемая поверхностной
энергией, пропорциональна площади
поверхности:
 ,
где
,
где - поверхностное натяжение.
- поверхностное натяжение.
Так как равновесное состояние характеризуется минимумом потенциальной энергии, то жидкость при отсутствии внешних сил будет принимать такую форму, чтобы при заданном объеме она имела минимальную поверхность, т.е. форму шара.
Поверхностный слой жидкости аналогичен растянутой упругой пленке, в которой действует силы натяжения.

Рисунок 48.2
Пусть
под действием сил поверхностного
натяжения поверхность жидкости стянулась,
(рис.48.2) при этом силы, действующие на
элемент
 контура, совершают работу
контура, совершают работу ,
где
,
где - сила поверхностного натяжения,
действующая на единицу длины контура
поверхности жидкости. Поскольку эта
работа совершается за счет уменьшения
поверхностной энергии
- сила поверхностного натяжения,
действующая на единицу длины контура
поверхности жидкости. Поскольку эта
работа совершается за счет уменьшения
поверхностной энергии ,
то
,
то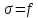 ,
т.е. поверхностное натяжение
,
т.е. поверхностное натяжение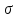 равно силе поверхности натяжения
приходящейся на единицу длины контура,
ограничивающего поверхность.
равно силе поверхности натяжения
приходящейся на единицу длины контура,
ограничивающего поверхность.
Единица поверхностного натяжения –ньютон на метр (Н/м) или джоуль на квадратный метр (Дж/м2).
