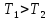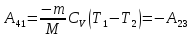- •Глава I. Физические основы механики
- •§ 1. Введение. Предмет физики. Методы физического исследования
- •§ 2. Роль физики в развитии техники и влияние техники на развитие физики
- •§ 3. Механика и её разделы. Система отсчета. Траектория, длина пути и вектор перемещения
- •§ 4. Скорость
- •§ 5. Ускорение и его составляющие
- •§ 6. Угловая скорость и угловое ускорение
- •Глава II. Динамика материальной точки
- •§ 7. Первый закон Ньютона.Масса. Импульс
- •§ 8. Второй закон Ньютона
- •§ 9. Третий закон Ньютона
- •§ 10. Закон сохранения импульса
- •§ 11. Принцип относительности Галилея. Преобразование Галилея
- •§ 12. Силы в механике
- •§ 13. Энергия. Работа и мощность
- •§ 14. Кинетическая и потенциальная энергия механической системы
- •§ 15. Закон сохранения и превращения энергии
- •§16. Удар абсолютно упругих и неупругих тел
- •Глава III. Механика твердого тела
- •§ 17. Момент инерции
- •§ 18. Кинетическая энергия вращения
- •§ 19. Момент силы. Основное уравнение динамики вращательного движения твердого тела
- •§ 20. Момент импульса и закон его сохранения
- •Глава IV. Основы молекулярной физики
- •§ 21. Основы молекулярно-кинетической теории газов
- •§ 22. Термодинамическое состояние тела
- •§ 23. Идеальный газ
- •§ 24. Уравнение состояния идеального газа
- •§ 25. Основное уравнение молекулярно-кинетической теории идеальных газов
- •§ 26. Скорости, характеризующие состояние газа
- •§ 27. Средняя длина свободного пробега молекул
- •§ 28. Явления переноса
- •Глава V. Основы термодинамики
- •§ 29. Внутренняя энергия термодинамической системы
- •§ 30. Число степеней свободы
- •§ 31. Первое начало термодинамики
- •§ 32. Работа газа при его расширении
- •§ 33. Теплоемкость
- •§ 34. Молярная теплоемкость при постоянном объеме
- •§ 35. Молярная теплоемкость при постоянном давлении. Уравнение Майера
- •§ 36. Применение первого начала термодинамики к изопроцессам
- •§ 37. Адиабатический процесс
- •§ 38. Политропические процессы
- •§ 39. Обратимые и необратимые процессы. Круговой процесс (цикл)
- •§ 40. Кпд кругового процесса
- •§ 41. Энтропия
- •§ 42. Второе начало термодинамики
- •§ 43. Третье начало термодинамики
- •§ 44. Тепловые двигатели и холодильные двигатели
- •§ 45. Теорема Карно.Цикл Карно
- •Глава VI. Реальные газы. Жидкости. Твердые тела
- •§ 46. Уравнение Ван-дер-ваальса
- •§ 47. Изотермы реальных газов
- •§ 48. Свойства жидкостей. Поверхностное натяжение
- •§ 49. Смачивание
- •§ 50. Капиллярность
- •§ 51. Явление капиллярности в быту, природе и технике
- •§ 52. Давление под искривленной поверхностью жидкости
- •§ 53. Кристаллические и аморфные твердые тела
- •§ 54. Изменение агрегатного состояния
- •§ 55. Фазовые переходы
- •§ 56. Диаграмма состояния
§ 43. Третье начало термодинамики
Третье
начало термодинамики – теорема
Нернста-Планка – постулирует поведение
термодинамических систем при нуле
кельвина (абсолютном нуле): энтропия
всех тел в состоянии равновесия стремится
к нулю по мере приближения температуры
к нулю Кельвина:
 .
.
§ 44. Тепловые двигатели и холодильные двигатели
Тепловой двигатель – это периодически действующий двигатель, совершающий работу за счет полученной извне теплоты.
Термостатом называется термодинамическая система, которая может обмениваться с теплотой с телами практически без изменения собственной температуры.
Рабочее тело – это тело, совершающее круговой процесс обменивающееся энергией с другими телами.
Принцип
работы теплового двигателя: от термостата
с более высокой температурой
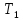 называемого нагревателем, за цикл
отнимается количество теплоты
называемого нагревателем, за цикл
отнимается количество теплоты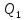 ,
а термостату с более низкой температурой
,
а термостату с более низкой температурой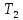 ,
называемому холодильником за цикл
передается количество теплоты
,
называемому холодильником за цикл
передается количество теплоты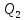 ,
при этом совершается работа
,
при этом совершается работа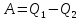 .
.
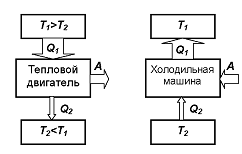
Рисунок 44.1
Термический КПД двигателя:
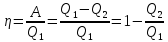 .
(44.1)
.
(44.1)
Чтобы
КПД был равен 1, необходимо, чтобы
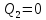 ,
а это запрещено вторым начало термодинамики.
,
а это запрещено вторым начало термодинамики.
Процесс,
обратный происходящему в тепловом
двигателе, используется в холодильной
машине: от термостата с более низкой
температурой
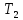 за цикл отнимается количество теплоты
за цикл отнимается количество теплоты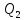 и отдается термостату с более высокой
температурой
и отдается термостату с более высокой
температурой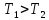 .
.
При
этом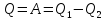 или
или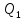 =
=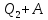 .
.
Количество
теплоты
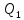 ,
отданное системой термостату
,
отданное системой термостату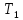 ,
больше количества теплоты
,
больше количества теплоты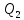 ,
полученного от термостата
,
полученного от термостата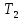 на величину работы, совершенной над
системой.
на величину работы, совершенной над
системой.
Эффективность
холодильной машины характеризует
холодильный коэффициент
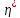 - отношение отнятой от термостата с
более низкой температурой количества
теплоты
- отношение отнятой от термостата с
более низкой температурой количества
теплоты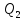 к работеА,
которая затрачивается на приведение
холодильной машины в действие
к работеА,
которая затрачивается на приведение
холодильной машины в действие
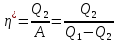 .
(44.2)
.
(44.2)
§ 45. Теорема Карно.Цикл Карно
Из
всех периодически действующих тепловых
машин, имеющих одинаковые температуры
нагревателей
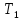 и холодильников
и холодильников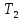 ,
наибольшим КПД обладают обратимые
машины. При этом КПД обратимых машин,
работающих при одинаковых температурах
нагревателей и холодильников, равны
друг другу и не зависят от природы
рабочего тела, а определяются только
температурами нагревателя и холодильника.
,
наибольшим КПД обладают обратимые
машины. При этом КПД обратимых машин,
работающих при одинаковых температурах
нагревателей и холодильников, равны
друг другу и не зависят от природы
рабочего тела, а определяются только
температурами нагревателя и холодильника.
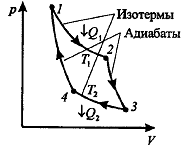
Рисунок 45.1
Наиболее экономичный обратимый круговой процесс, состоящий из двух изотерм и двух адиабат.
Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.
Последовательные термодинамические процессы в цикле Карно: 1-изотерма-2-адиабата-3-изотерма-4-адиабата-1.
|
Изотермическое расширение 1-2
|
|
|
Адиабатическое расширение 2-3
|
|
|
Изотермическое сжатие 3-4
|
|
|
Адиабатическое сжатие
|
|
Работа, совершаемая в результате кругового процесса
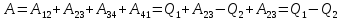
Для
адиабат 2-3 и 4-1 уравнения Пуассона
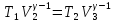 ,
,
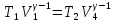 откуда
откуда
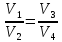
Используя
это, термический КПД цикла Карно: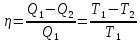 .
.
Глава VI. Реальные газы. Жидкости. Твердые тела
§ 46. Уравнение Ван-дер-ваальса
При рассмотрении реальных газов необходимо учитывать собственный объем молекул и силы межмолекулярного взаимодействия.
Силы
межмолекулярного взаимодействия –
короткодействующие – они проявляются
на расстояниях менее
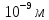 .
Сила взаимодействия молекул – это
равнодействующая сил притяжения
.
Сила взаимодействия молекул – это
равнодействующая сил притяжения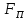 (они преобладают на больших расстояниях)
и сил отталкивания
(они преобладают на больших расстояниях)
и сил отталкивания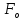 (они доминирует на малых расстояниях).
(они доминирует на малых расстояниях).
На
расстоянии
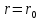 эти силы уравновешивают друг друга и
эти силы уравновешивают друг друга и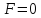 .
Таким образом, расстояние
.
Таким образом, расстояние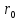 - это равновесие расстояние между
молекулами, на котором бы они находились
в отсутствие теплового движения.
Потенциальная энергия взаимодействия
молекулUминимальна
в состоянии устойчивого равновесия при
- это равновесие расстояние между
молекулами, на котором бы они находились
в отсутствие теплового движения.
Потенциальная энергия взаимодействия
молекулUминимальна
в состоянии устойчивого равновесия при
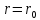 .
.
Рисунок
46.1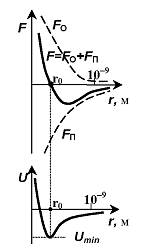
Соотношение
между
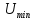 и
и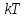 является критерием различных агрегатных
состояний.
является критерием различных агрегатных
состояний.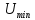 определяет
работу, которую нужно совершить против
сил притяжения, чтобы разъединить
молекулы, находящиеся в равновесии.
определяет
работу, которую нужно совершить против
сил притяжения, чтобы разъединить
молекулы, находящиеся в равновесии.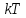 определяет удвоенную среднюю энергию,
приходящуюся на одну степень свободы
теплового движения молекул.
определяет удвоенную среднюю энергию,
приходящуюся на одну степень свободы
теплового движения молекул.
При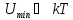 вещество
находится в газообразном состоянии,
т.к. тепловое движение молекул препятствует
соединению (конденсации) молекул.
вещество
находится в газообразном состоянии,
т.к. тепловое движение молекул препятствует
соединению (конденсации) молекул.
При вещество
находится в твердом состоянии, т.к.
тепловой энергии недостаточно чтобы
«оторвать» молекулы друг от друга.
вещество
находится в твердом состоянии, т.к.
тепловой энергии недостаточно чтобы
«оторвать» молекулы друг от друга.
При
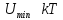 вещество находится в жидком состоянии,
т.к. в результате теплового движения
молекулы перемещаются в пространстве,
обмениваясь местами, но не расходясь
на расстояния, превышающие
вещество находится в жидком состоянии,
т.к. в результате теплового движения
молекулы перемещаются в пространстве,
обмениваясь местами, но не расходясь
на расстояния, превышающие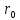 .
.
Наиболее простым и качественно верно отображающим поведение реального газа, является уравнение Ван-дер-Ваальса:
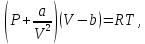 (46.1)
(46.1)
а, b – постоянные величины, первая учитывает силы взаимодействия, вторая учитывает размер молекул.
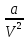 –характеризует
добавочное давление, под которым
находится реальный газ вследствие сил
сцепления между молекулами и называется
внутренним давлением.
–характеризует
добавочное давление, под которым
находится реальный газ вследствие сил
сцепления между молекулами и называется
внутренним давлением.
Для произвольной массы газа:
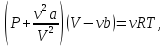
где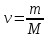 .
.
Уравнение Ван-дер-Ваальса качественно верно отображает поведение жидких и газообразных веществ, для двухфазных состояний оно неприменимо.
На PV – диаграмме (рис.46.2) показаны изотермы, построенные по уравнению Ван-дер-Ваальса. Из кривых видно, что при сравнительно низких температурах имеются волнообразные участки. Чем выше температура, тем короче эти части кривых. Эти волнообразные кривые указывают на непрерывный переход от жидкого состояния в парообразное при данной температуре. Точка А соответствует состоянии жидкости, точка В относится парообразному состоянии вещества.
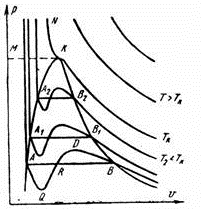
Рисунок 46.2
В действительности переход из жидкого состояния в парообразное всегда происходит через двухфазное состояние вещества. При этом при данной температуре процесс перехода происходит также и при постоянном давлении. Этот действительный переход из жидкого состояния в парообразное изображается прямой линией АВ.
Практически для особо чистых веществ возможно осуществление участков волнообразной кривой AQ и DB. В первом случае имеют место неустойчивые состояния перегретой жидкости, а во втором – переохлажденного пара.
При определенной температуре изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка (точка К). Эту температуру называют критической. Если соединить точки А1, А2, А3 … и В1, В2, В3… получим кривую похожую на параболу.
Кривая АК называется нижней пограничной кривой и соответствует состоянию кипения жидкости. Кривая КВ называетсяверхней пограничной кривой и соответствует состояния сухого насыщенного пара.
Таким образом, для реального вещества PV – диаграмму можно разбить на 3 области:
1 – область жидкого состояния, расположена левее нижней пограничной кривой;
2 – область двухфазных состояний (влажный пар), расположена между нижней и верхней пограничной кривой);
3 – область перегретого пара, расположена правее верхней пограничной кривой и выше критической точки.
Условно область жидкости ограничивают сверху линией КМ – критическая изобара.
Критическую температуру Д.И.Менделеев называл абсолютной температурой кипения, при которой поверхностное натяжение в жидкости становится равным нулю, т.е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщенным паром).

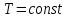 ,
,
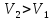
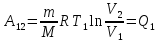
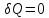 ,
,
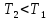
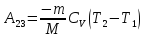
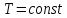 ,
,
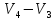
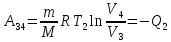
 ,
,