
- •Глава I. Физические основы механики
- •§ 1. Введение. Предмет физики. Методы физического исследования
- •§ 2. Роль физики в развитии техники и влияние техники на развитие физики
- •§ 3. Механика и её разделы. Система отсчета. Траектория, длина пути и вектор перемещения
- •§ 4. Скорость
- •§ 5. Ускорение и его составляющие
- •§ 6. Угловая скорость и угловое ускорение
- •Глава II. Динамика материальной точки
- •§ 7. Первый закон Ньютона.Масса. Импульс
- •§ 8. Второй закон Ньютона
- •§ 9. Третий закон Ньютона
- •§ 10. Закон сохранения импульса
- •§ 11. Принцип относительности Галилея. Преобразование Галилея
- •§ 12. Силы в механике
- •§ 13. Энергия. Работа и мощность
- •§ 14. Кинетическая и потенциальная энергия механической системы
- •§ 15. Закон сохранения и превращения энергии
- •§16. Удар абсолютно упругих и неупругих тел
- •Глава III. Механика твердого тела
- •§ 17. Момент инерции
- •§ 18. Кинетическая энергия вращения
- •§ 19. Момент силы. Основное уравнение динамики вращательного движения твердого тела
- •§ 20. Момент импульса и закон его сохранения
- •Глава IV. Основы молекулярной физики
- •§ 21. Основы молекулярно-кинетической теории газов
- •§ 22. Термодинамическое состояние тела
- •§ 23. Идеальный газ
- •§ 24. Уравнение состояния идеального газа
- •§ 25. Основное уравнение молекулярно-кинетической теории идеальных газов
- •§ 26. Скорости, характеризующие состояние газа
- •§ 27. Средняя длина свободного пробега молекул
- •§ 28. Явления переноса
- •Глава V. Основы термодинамики
- •§ 29. Внутренняя энергия термодинамической системы
- •§ 30. Число степеней свободы
- •§ 31. Первое начало термодинамики
- •§ 32. Работа газа при его расширении
- •§ 33. Теплоемкость
- •§ 34. Молярная теплоемкость при постоянном объеме
- •§ 35. Молярная теплоемкость при постоянном давлении. Уравнение Майера
- •§ 36. Применение первого начала термодинамики к изопроцессам
- •§ 37. Адиабатический процесс
- •§ 38. Политропические процессы
- •§ 39. Обратимые и необратимые процессы. Круговой процесс (цикл)
- •§ 40. Кпд кругового процесса
- •§ 41. Энтропия
- •§ 42. Второе начало термодинамики
- •§ 43. Третье начало термодинамики
- •§ 44. Тепловые двигатели и холодильные двигатели
- •§ 45. Теорема Карно.Цикл Карно
- •Глава VI. Реальные газы. Жидкости. Твердые тела
- •§ 46. Уравнение Ван-дер-ваальса
- •§ 47. Изотермы реальных газов
- •§ 48. Свойства жидкостей. Поверхностное натяжение
- •§ 49. Смачивание
- •§ 50. Капиллярность
- •§ 51. Явление капиллярности в быту, природе и технике
- •§ 52. Давление под искривленной поверхностью жидкости
- •§ 53. Кристаллические и аморфные твердые тела
- •§ 54. Изменение агрегатного состояния
- •§ 55. Фазовые переходы
- •§ 56. Диаграмма состояния
§ 25. Основное уравнение молекулярно-кинетической теории идеальных газов
Пусть
в сосуде объемом V
находится идеальный газ массой m,
состоящий из N
молекул массой m0,
движущихся с одинаковыми скоростями
v.
Концентрация молекул в газе по определению
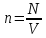 .
.
Если
при соударении со стенками за время
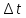 элементарной площадке
элементарной площадке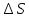 в стенки сосуда передается импульс
в стенки сосуда передается импульс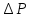 ,
то давление газа, оказываемое им на
стенки сосуда
,
то давление газа, оказываемое им на
стенки сосуда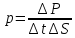 .
.
При
каждом соударении молекула, движущаяся
перпендикулярно стенке, передает ей
импульс
 .
В среднем по направлению к стенке
движется 1/6 часть всех молекул. Если
рассмотреть три взаимно перпендикулярные
оси, то в среднем только 1/3 молекул
движется вдоль одной из осей и только
половина из них ½(1/3) вдоль данного
направления. Поэтому, за время
.
В среднем по направлению к стенке
движется 1/6 часть всех молекул. Если
рассмотреть три взаимно перпендикулярные
оси, то в среднем только 1/3 молекул
движется вдоль одной из осей и только
половина из них ½(1/3) вдоль данного
направления. Поэтому, за время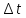 площадки
площадки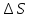 достигнут
достигнут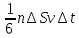 молекул и передадут ей импульс
молекул и передадут ей импульс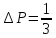 n
n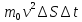 .
.
Давление,
оказываемое газом на стенку сосуда
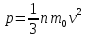 .
.
Если скорости молекул различны, то необходимо использовать среднюю квадратичную скорость.
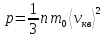 -
основное
уравнение МКТ идеальных газов.
(25.1)
-
основное
уравнение МКТ идеальных газов.
(25.1)
С
учетом соотношений
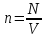 и
и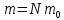 следует:
следует:
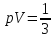 N
N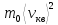
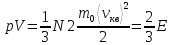 .
.
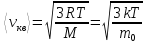 ,
,
где
использовано
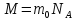 и
и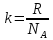 .
.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:
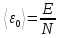 =
=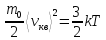 .
(25.2)
.
(25.2)
Отсюда
следует, что при
Т= 0К,
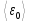 = 0 – прекращается движение молекул
газа.
= 0 – прекращается движение молекул
газа.
Молекулярно-кинетическое толкование температуры: термодинамическая температура – есть мера средней кинетической энергии поступательного движения молекул газа.
§ 26. Скорости, характеризующие состояние газа
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью.
Наиболее
вероятная скорость
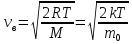 ;
;
Средняя
арифметическая скорость
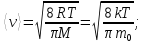
Средняя
квадратичная скорость
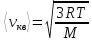 .
.
Каково же распределение молекул в поле потенциальных сил? Эта задача была решена Больцманом, выдающимся австрийским физиком.

Рисунок 26.1
Рассмотрим
изменение давления в столбе воздуха,
находящегося в поле тяготения Земли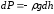 ,
где
знак " - " указывает на уменьшение
давления
,
где
знак " - " указывает на уменьшение
давления
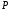 с ростом высотыh.
с ростом высотыh.
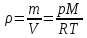
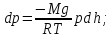
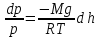 .
.
С изменением высоты от h0до hдавление изменяется от р0 до р
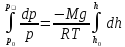
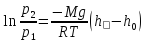
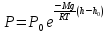 .
(26.1)
.
(26.1)
Выражение (26.1) называется барометрической формулой.
Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение (26.1) может быть записано в виде
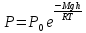 (26.2)
(26.2)
Прибор для определения высоты над земной поверхностью называется высотометром (или альтиметром). Из формулы (26.2) следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.
Барометрическую формулу можно преобразовать, если воспользоваться выражением p=nkT
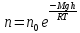 ,
где n–
концентрация молекул на высоте h,
n0–
концентрация на высоте h=0.
,
где n–
концентрация молекул на высоте h,
n0–
концентрация на высоте h=0.
Так
как
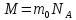 ,
а
,
а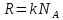 то
то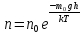 ,
где
,
где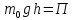 - потенциальная энергия молекулы:
- потенциальная энергия молекулы:
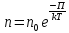 называется
распределением Больцмана. (26.3)
называется
распределением Больцмана. (26.3)
Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
