• Волновое уравнение для плоской гармонической волны. Его решение.

Волна – процесс распространения колебаний в пространстве с течением времени. Основной отличительной особенностью волны является перенос энергии без переноса вещества.

Поляризация света — это процесс, при котором световые волны направляются в определённой плоскости, ограничиваясь одним направлением колебаний (Линейная, круговая, эллиптическая).

Ψ (0,t) = A cos(ωt + φ_o) - закон колеб. источника.

Ψ(х ,t) = A cos (ωt - kx + φ_o)

Ψ(х ,t) = А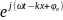

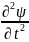= υ²

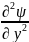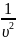+ + = (произв.направ.)

Частицы среды, расположенные на расстоянии x, отстают по фазе на kx от источника.

В трёхмерном случае решение обобщается с использованием волнового вектора k⃗:

• Фазовая скорость, частота и волновое число.

Фазовая скорость — это скорость перемещения точки, обладающей постоянной фазой колебательного движения, вдоль направления распространения волны. Фазовая скорость может превышать скорость света.

υ = = fλ= ω/k= – фазовая скорость

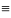
В вакууме ε =1, μ =1, соответственно υ_ф 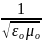= с – скорости света

В среде υ_ф = .

Частота (ν,f) — это физическая величина (Гц), равная количеству повторяющихся событий (например, колебаний) в единицу времени. Она обратно пропорциональна периоду T:

ν=1/T

Волновое число (k) — это пространственный аналог частоты, характеризующий число колебательных периодов на единицу длины. Волновое число также можно определить как скорость изменения фазы по пространственной координате.

k=2π/λ или k=dφ/dx (рад/м)

• Уравнения сферической и цилиндрической волн.

Сферическая: такая волна порождается точечным источником и распространяется во все стороны, амплитуда её уменьшается обратно пропорционально расстоянию, поскольку энергия проходит через бόльшую поверхность.

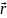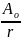Ψ( ,t) = cos (ωt – )

Цилиндрическая: волна порождается протяжённым источником колебаний (нить, тонкий цилиндр). ρ – полярный радиус.

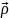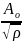Ψ( ,t) = = cos (ωt – ),

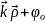• Дисперсионное соотношение для волн.

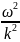υ² = υ² =

- определяет связь фазовой скорости, циклической частоты и волнового числа

• Нормальная и аномальная дисперсия сред.

Дисперсия – зависимость фазовой скорости от частоты (волнового числа).

П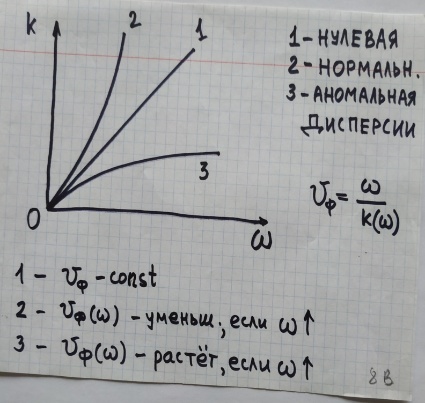 ри нормальной дисперсии показатель преломления n увеличивается с р.частоты ω (или при ум. λ). Фазовая скорость света в среде уменьшается с увеличением частоты. Хар-на для прозрачных областей спектра, где поглощение света минимально.

При аномальной дисперсии показатель преломления n уменьшается с р. частоты ω (или ув. с р.λ). Наблюдается в областях спектра, близких к полосам поглощения, где взаимодействие света с веществом сильно влияет на показатель преломления.

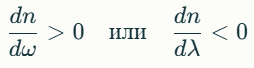
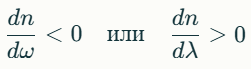
• Плоская гармоническая электромагнитная волна. Характер изменения электрической и магнитной составляющих. Связь амплитуд этих волн.

ПГЭМВ — это решение волнового уравнения Максвелла, в котором ЭП и МП распространяются в виде ГК с плоскими фронтами волны. Поверхности равной фазы (фронты волны) представляют собой плоскости, перпендикулярные направлению распространения волны.

В вакууме или однородной изотропной среде плоская электромагнитная волна описывается векторными функциями электрического поля E и магнитного поля H, которые зависят от времени и координат по гармоническому закону.

Волна является поперечной, то есть векторы E и H перпендикулярны направлению распространения волны, заданному вектором k.

Связь на рисунке с корнями.

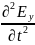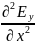
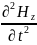= υ²

= υ²