• Энергия гармонических (г) и квазигармонических (к) колебаний на примере идеального (и) и реального (р) эл. Контуров.

1. ГИ: Идеальный электрический колебательный контур состоит из индуктивности L и ёмкости C без сопротивления (то есть без потерь энергии). В таком контуре происходят гармонические колебания — периодический обмен энергией между магнитным полем катушки и электрическим полем конденсатора.

2. КР: В реальном контуре есть активное сопротивление RR, которое приводит к потерям энергии — часть энергии рассеивается в виде тепла.

3. Для тупых:

-В идеальном контуре энергия колебаний не меняется — она "перетекает" между магнитным полем катушки и электрическим полем конденсатора, и колебания продолжаются бесконечно.

-В реальном контуре часть энергии теряется из-за сопротивления, поэтому амплитуда колебаний уменьшается, и колебания затухают. -Затухание происходит по экспоненте — амплитуда уменьшается в e раз за время, равное обратному коэффициенту затухания.

• Понятие о нелинейных кол. И колебаниях других типов.

Нелинейные колебания — это колебания в системах, где законы, описывающие движение, не являются линейными. Это значит, что сила, воздействующая на систему, не пропорциональна смещению или скорости, а может зависеть от них сложным образом.

• В таких системах параметры, например сопротивление, индуктивность или ёмкость, могут зависеть от напряжения, тока, температуры или других факторов. Это приводит к тому, что уравнения движения становятся нелинейными.

• В результате нелинейности колебания могут иметь сложную форму, отличную от простой синусоиды, могут появляться дополнительные гармоники, субгармоники, а также возможны явления автоколебаний и хаоса.

Примеры нелинейных элементов в электрических цепях

• Диоды — ток через них зависит от направления и величины напряжения нелинейно.

• Транзисторы — имеют сложные характеристики, зависящие от трёх выводов, и используются для усиления сигналов.

• Термисторы — сопротивление зависит от температуры, что создаёт нелинейность.

• Стабилитроны (диоды Зенера) — имеют резкий переход в режиме пробоя, что тоже нелинейно.

Эти элементы вызывают нелинейное поведение цепи, что влияет на форму и спектр колебаний

Особенности нелинейных колебаний

• В нелинейных системах колебания могут быть автоколебаниями — незатухающими колебаниями, которые возникают без внешнего периодического воздействия. Амплитуда и частота таких колебаний определяются свойствами самой системы, а не внешним сигналом7.

• Нелинейность приводит к изменению формы сигнала: при подаче синусоидального напряжения ток в цепи с нелинейным элементом становится несинусоидальным, появляются высшие гармоники и искажения.

• В некоторых случаях возникают непериодические колебания или даже хаотические режимы.

Другие типы колебаний

• Линейные колебания — описываются линейными дифференциальными уравнениями, имеют синусоидальную форму, амплитуда и частота не зависят от времени (если нет затухания).

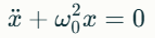
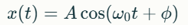
• Затухающие колебания — амплитуда уменьшается со временем из-за потерь энергии (например, сопротивления).

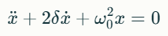
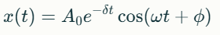
• Вынужденные колебания — возникают под действием внешнего периодического воздействия.

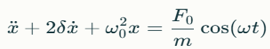
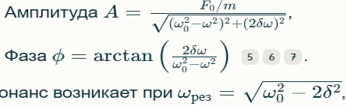
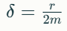
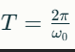
• Автоколебания — Это особый вид колебаний, когда система получает энергию от постоянного источника, причём сама регулирует её поступление. Различают релаксационные и томсоновские авт.колебания. Система самовозбуждается при условии:

(dε/dt)_пост.  > (dε/dt)_потерь  

• П 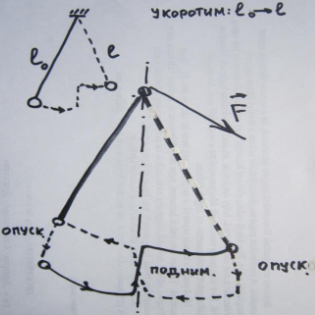араметрические – Имеется способ возбуждения системы, когда целенаправленно изменяются параметры системы – индуктивность или емкость контура, длина нити маятника и т.п. Момент инерции маятника   I = m ℓ² , причём  ℓ_о  > ℓ  ⇒  ∆I = m ℓ_о² - m ℓ² 

Волны (23)