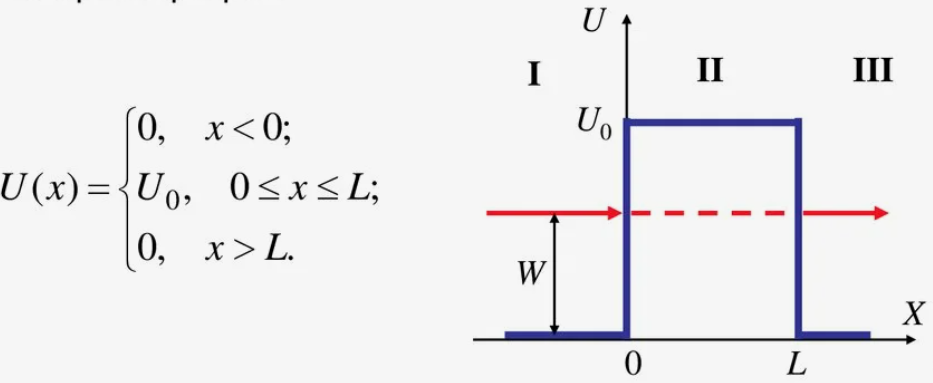
• Потенциальный барьер в квантовой механике. Укажите области разного поведения потенциальной энергии от координаты. Дайте примеры таких барьеров.

Потенциальный барьер — это область пространства, где потенциальная энергия частицы выше, чем в соседних областях. В квантовой механике такие барьеры играют ключевую роль в явлениях туннелирования и отражения, которые невозможны с точки зрения классической физики (1 и 3 область – пот.эн. минимальна, 2 – барьер и повышенная энергия).

Ψ_II = e ^{- δx} + De ^δx (D=0)

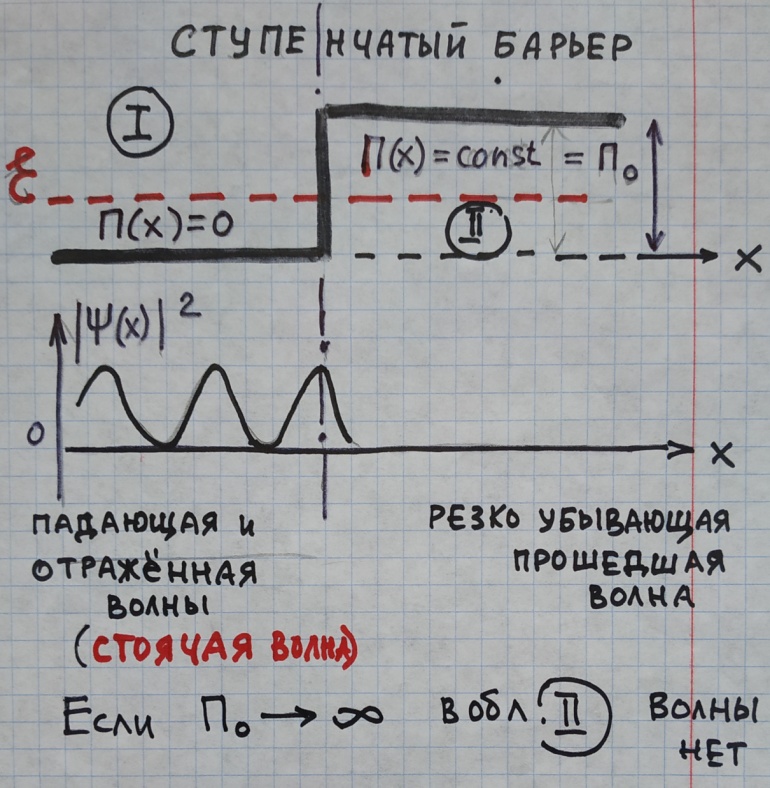
• Условия налагаемые на - функцию в потенциальном поле с барьерами на границах разной зависимости п(х)?

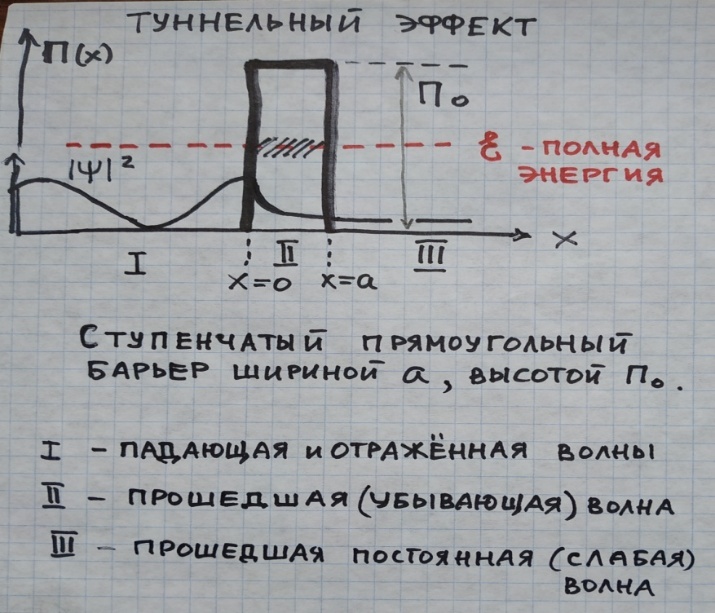
• Туннельный эффект. В чём состоит явление и чем его можно характеризовать?

Туннельный эффект — это квантовомеханическое явление, при котором частица с энергией, меньшей высоты потенциального барьера, имеет ненулевую вероятность пройти сквозь этот барьер, хотя классическая физика такое прохождение запрещает.

В чём состоит явление

• В классической механике частица, энергия которой меньше высоты барьера, не может преодолеть этот барьер.

• В квантовой механике волновая функция частицы не обнуляется внутри барьера, а экспоненциально затухает, что приводит к ненулевой вероятности обнаружить частицу по другую сторону барьера — это и есть туннелирование.

• Туннельный эффект наблюдается в системах с потенциальными барьерами конечной ширины и высоты, например, в молекулах (инверсия аммиака), туннельных диодах, радиоактивном распаде и химических реакциях.

Чем характеризуется туннельный эффект

• Коэффициентом прохождения — вероятность того, что частица пройдет через барьер. Для простого прямоугольного барьера он экспоненциально мал и зависит от ширины и высоты барьера, а также массы и энергии частицы.

• Коэффициентом отражения — вероятность отражения частицы от барьера.

• Временем туннелирования — временем, за которое частица "преодолевает" барьер (этот вопрос остается предметом дискуссий в современной науке).

• Спектральным расщеплением — в некоторых системах (например, двойная потенциальная яма) туннелирование приводит к расщеплению энергетических уровней.

Область I (П=0)

Получим: Ψ_I = e ^{– jkx} + Be ^jkx ,

где В определяет амплитуду отражённой волны, k = .

Область II (П_о )

Внутри барьера волна затухает

Ψ_II De ^{– δx} , δ = (2.7)

Область III (П=0)

Здесь существует бегущая волна

Ψ_III De ^{– δa} e ^{– jkx}

Вводят коэфф. пропускания барьера Т:

Т = = e ^{– 2δa} = exp (-2a ) (2.8)