• Формула де Бройля.

Физический смысл формулы в том, что квантовый объект можно рассматривать как частицу с определённым количеством движения (импульсом), а также как волну с длиной, которая определяется этим уравнением.

λ_Б =

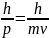
• Соотношение неопределённостей Гейзенберга.

Невозможно одновременно точно определить координаты и импульс движущегося в атоме е в силу его волновых св-в.

Δx⋅Δp_x ≥ℏ,

ΔE⋅Δt ≥ℏ (с. Гейзенберга)

• Δx — неопределённость координаты (x/y/z),

• Δp — неопределённость импульса,

• ℏ=h/2π — приведённая постоянная Планка.

• ΔE – неопределенность энергии стационарного состояния системы

• Δt – промежуток времени, в котором сущ. система

Чем точнее мы измеряем положение частицы, тем менее точно можно определить её импульс, и наоборот. Это ограничение связано с волновой природой микрочастиц: локализация частицы в пространстве приводит к расширению спектра её волновых чисел (импульсов)

Длина волны де Бройля частицы связана с её импульсом следующим образом:

• Волновая функция для микрочастиц в квантовой механике. Волновая функция де Бройля (пси-функция). Условие нормировки волновой функции в квантовой механике.

  • Ψ_Б (r,t) = A е ^{j(pr –ωt)} dw =│ψ│² dV – вол.ф-я

с учётом ℇ = ħω, 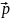= ħ : Ψ_Б (r,t) = A 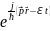- для свободного движения частицы.

Условие нормирования:

dw =│ψ│² d ³r, где d ³r =dx dy dz

• Определение средних и собственных значений физических величин с использованием пси-функции.

Если волновая функция Ψ является собственным состоянием оператора A^, то при действии оператора на Ψ получается:

где a — собственное значение оператора A^.

Если состояние системы задано волновой функцией ΨΨ, которая не обязательно является собственным состоянием оператора A^, среднее значение величины AA вычисляется как:

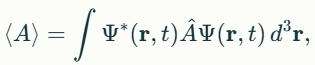
• Оператор проекции импульса в квантовой механике. Результат действия этого оператора на собственную волновую 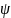- функцию. Какие другие операторы используются?

1) Операторы проекции импульса:

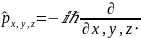
Общий вид оператора импульса:

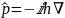
На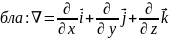

2)

3)

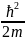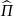*) - + (r)= 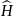– оператор (Гамильтона) полной энергии

**)

• Квантование энергии, момента импульса.

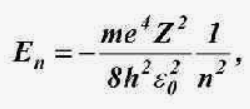
Принцип квантования энергии гласит, что любая система взаимодействующих частиц, способная образовывать стабильное состояние, может сделать это только при определённых значениях энергии. Система может находиться только в состояниях с определёнными уровнями энергии, причём основное состояние всегда наиболее вероятно.

• Спин микрочастиц (электрона). Квантовые числа.

Спин — внутренняя собственная угловая моментная характеристика частицы, не связанная с её движением в пространстве. Это фундаментальное квантовое свойство, которое проявляется, например, в магнитном моменте электрона и его взаимодействии с магнитными полями.

Для электрона спин равен s=1/2 (полуцелое значение), что означает, что электрон является фермионом.

• Стационарное уравнение Шредингера. Пределы его применимости, и для каких задач используется?

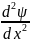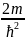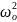
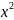+ (ℇ - m ) ψ =0

Пределы применимости:

• Для замкнутых квантовых систем с неизменяющимся во времени гамильтонианом (потенциал не зависит от времени).

• Используется для описания стационарных состояний — состояний с определённой энергией.

• Не применимо для систем с явно зависящим от времени потенциалом или при необходимости учёта релятивистских эффектов.

Для каких задач используется:

• Квантовые частицы в потенциальных ямах (например, бесконечно глубокая яма, гармонический осциллятор).

• Движение электрона в атоме водорода и других атомных системах.

• Квантовые туннельные эффекты.

• Анализ энергетического спектра молекул, кристаллов и наноструктур.

• Возмущённые задачи (расчёт поправок к энергии и волновым функциям при небольших изменениях потенциала)