ВОПРОСЫ к ЭКЗ. 2025

Колебания (11):

• Дифф. Уравнения гармонических, квазигармонических (затухающих) и вынужденных колебаний для различных колебательных систем. Их решения.

1. 

У физ.маятника + ω_o² α= 0/ + 2δ + ω_o² α = 0 (нет/есть момент сил трения)

tg φ_o = - + 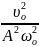= 1

2. 

В эл. Контуре: + 2 δ + ω_o² q = 0, δ = , ω_o² =

3. 

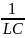
фи -фазовый сдвиг между вынуждающей силой и смещением

А = = ! tg ψ = ! ω_рез.=

Для К. заряда в контуре: q_m(ω) =

R_c = , = - реактивные сопротивления (см. билет импеданс)

• Характеристики затухающих колеб.

З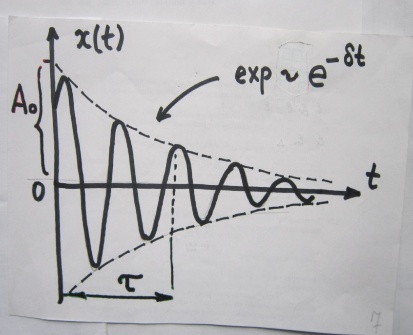 атухающие колебания — это колебания, амплитуда которых со временем уменьшается из-за потерь энергии в системе (трение, внутреннее сопротивление, излучение и др.)

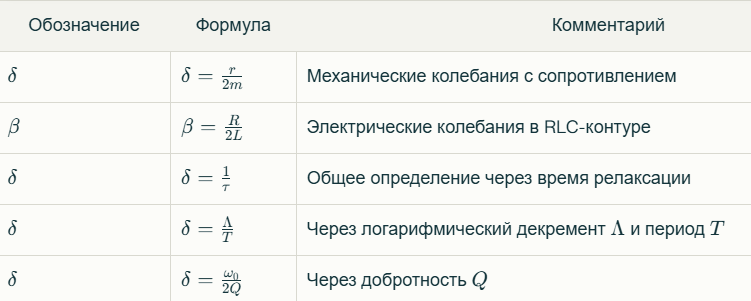
Основные характеристики затухающих колебаний

• Амплитуда Максимальное отклонение от положения равновесия, которое с течением времени убывает по экспоненциальному закону:

А = A_o е^{- δt}

• Период колебаний Время одного полного колебания. При малом затухании период почти не меняется и близок к собственному периоду системы 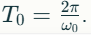При увеличении затухания период может увеличиваться, а при сильном затухании колебания переходят в апериодическое движение.

• Коэффициент затухания (δ) Характеризует скорость уменьшения амплитуды колебаний. Он обратен времени релаксации τ — времени, за которое амплитуда уменьшается в e раз:

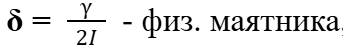
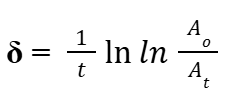
Коэффициент затухания связан с логарифмическим декрементом затухания Λ и периодом T  = δ∙Т и добротностью Q

• Логарифмический декремент затухания (Λ) Натуральный логарифм отношения амплитуд двух последовательных максимумов, отстоящих на период T:

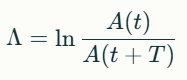
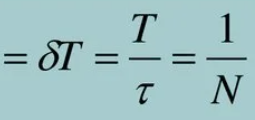
• Время релаксации (τ) Время, за которое амплитуда уменьшается в e раз. Это показатель скорости затухания колебаний:

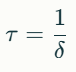
• Частота затухающих колебаний (ω) При затухании собственная частота изменяется:

ω =

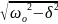
где ω0ω0 — собственная частота незатухающих колебаний. При малом затухании ω≈ω0

• Энергия колебаний Энергия затухающих колебаний уменьшается по экспоненте с удвоенным коэффициентом затухания:

• Добротность системы и её выражения.

Добротность Q — это безразмерная величина, которая определяется как отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания: . Она показывает, насколько эффективно система сохраняет энергию колебаний по сравнению с потерями.

Физический смысл

• Чем выше добротность, тем меньше потери энергии за период колебаний и тем медленнее затухают колебания.

• Добротность характеризует остроту резонанса: высокая Q означает узкий и высокий пик резонансной амплитуды.

• Добротность обратно пропорциональна скорости затухания колебаний.

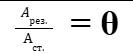(вын.к.)

θ = 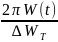-равна отношению энергии в данный момент к её изменению за период, умноженной на 2π

• Представление колебательной функции в комплексной форме.

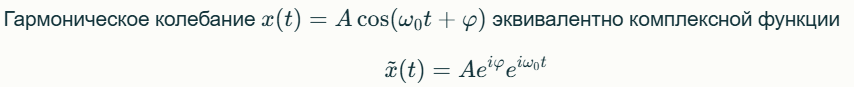
• Релаксация затухающих колебаний.

Релаксация — это затухание колебаний с экспоненциальным уменьшением амплитуды. В реальных системах энергия колебаний рассеивается (например, из-за трения или электрических потерь), поэтому амплитуда колебаний с течением времени уменьшается.

Амплитуда затухающих колебаний уменьшается по экспоненциальному закону во времени: А = A_o е^{- δt} 

Время, за которое амплитуда уменьшается в e≈2,718 раз, называется временем релаксации или временем жизни колебаний: τ =1/δ. Физический смысл времени релаксации

• Время релаксации показывает, как быстро колебания теряют энергию и затухают. Чем меньше τ, тем быстрее амплитуда уменьшается.

• При малом затухании время релаксации значительно больше периода колебаний T, то есть колебания совершают много циклов, прежде чем амплитуда существенно снизится.

• За время релаксации амплитуда уменьшается в ee раз, а энергия, пропорциональная квадрату амплитуды, уменьшается примерно в e²≈7,4.