2 курс / Анализ данных / Методические рекомендации по подготовке к контрольной работе (ТВиМС)

но также, что 40% всех работников фирмы составляют женщины. Выяс-

нить, существует ли на фирме дискриминация женщин в оплате труда.

5. Теорема умножения

Для произвольных событий A и B имеют место следующие правила вычисления вероятности их произведения:

( ∩ ) = ( ) ( | ) = ( ) ( | ).

Для трех событий:

( ∩ ∩ ) = ( ) ( | ) ( | ∩ ).

Пример 13. В урне 4 красных, 3 синих и 1 зеленый шар. Из урны наугад поочередно извлекается один шар и откладывается в сторону.

Найти вероятность того, что впервые красный шар будет извлечен не позднее, чем на третьем шаге.

Решение. Разберем все варианты, при которых красный шар появится не позднее третьего шага. Обозначим буквами «к», «с» и «з» появление соответственно красного, синего и зеленого шаров. Подходя-

щие варианты:

{к}, {ск}, {зк}, {сск}, {сзк}, {зск}.

Вероятность осуществления вариантов со второго по шестой

находится по теореме умножения. Например,

({cck}) = (первый синий) ∙ (второй синий|первый синий) ∙

21

1 3 4 1({зсk}) = 8 ∙ 7 ∙ 6 = 28.

Отдельные варианты являются несовместными событиями, и

искомая вероятность находится по теореме сложения:

Задачи для самостоятельного решения

23. Из корзины, содержащей три красных яблока и семь зеленых,

вынимают по очереди два яблока. Найдите вероятность того, что оба они будут красными.

24. Вероятность попадания в цель для первого стрелка равна 0, 8,

для второго – 0, 7, для третьего – 0, 9. Каждый из стрелков делает по одному выстрелу. Какова вероятность того, что в мишени три пробоины?

25. В урне 3 белых, 5 черных и 2 красных шара. Из урны вынимают один за другим все находящиеся в ней шары и записывают их цвета. Найти вероятность того, что в этом списке белый цвет появится раньше черного.

22

6. Формула полной вероятности

События , , … , составляют полную группу, если все они попарно несовместны и в сумме составляют все пространство элемен-

тарных событий,

( ) = ∑ ( ) ( | ).

=1

Пример 14. Из корзины, содержащей три красных яблока и семь зеленых, вынимают по очереди все яблоки. Найдите вероятность того,

что вторым по счету будет вынуто красное яблоко.

Решение. Обозначим события: A – «Вторым по счету − красное»,

1 = «Первым по счету − красное», 2 = «Первым по счету − зеленое».

По формуле полной вероятности

( ) = ( 1) ( | 1) + ( 2) ( | 2) = 103 ∙ 29 + 107 ∙ 39 = 103 .

Пример 15. Проводится тестирование остаточных знаний по математике 10% вопросов проверяют знание линейной алгебры, 20% –

23

знание математического анализа, остальные – знание теории вероятностей. Студент считает, что вероятности того, что он не ответит на вопрос теста, составляет для указанных групп вопросов 0,01, 0,05

и 0,2 соответственно. Найдите ожидаемый процент вопросов теста, на которые не ответит студент.

Решение. Введем события: A – «Студент не ответит на вопрос»,

1 – «вопрос по линейной алгебре», 2 – «вопрос по математи-

ческому анализу», 3 – «вопрос по теории вероятностей». По формуле полной вероятности

3

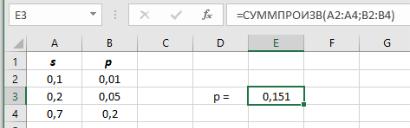
( ) = ∑ ( ) ( | ) = 0,1 ∙ 0,01 + 0,2 ∙ 0,05 + 0,7 ∙ 0,2 = 0,151.

=1

В Excel сумма произведений элементов двух массивов вычис-

ляется по команде СУММПРОИЗВ.

Задачи для самостоятельного решения

26. Имеются три одинаковые с виду урны. В первой – 4 белых шара и 8 черных; во второй – 6 белых и 3 черных; в третьей – только белые шары. Выбирается наугад одна из урн и из нее случайным образом извлекается один шар. Найти вероятность того, что этот шар белый.

24

27. Вероятность того, что дневной оборот продавца мороженого превысит 20 000 руб., при солнечной погоде равна 80%, при переменной облачности – 50%, а при пасмурной погоде – 10%. Найдите вероятность того, что на следующий день оборот превысит 20 000 руб., если вероятность солнечной погоды в данное время года составляет 20%,

вероятность переменной облачности и вероятность пасмурной погоды – по 40%.

28. Группа студентов состоит из 5 отличников, 10 хорошо успевающих и 9 занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность того, что он получит хорошую или отличную оценку.

29. Летчик катапультируется в местности, 80% которой занимают леса. Вероятность благополучного приземления в лесу равна 0,3, а в безлесной местности – 0,98. Какова вероятность благополучного при-

земления летчика?

30. В магазине проходит бесплатная дегустация газированного напитка, Вероятность того, что участвовать в дегустации согласится посетитель – мужчина, составляет 0,1, а вероятность того, что участвовать в дегустации согласится – женщина, равна 0,2. Сейчас в магазине находятся пятнадцать женщин и десять мужчин. Девушка – промоутер обратилась с предложением принять участие в дегустации к

25

двум посетителям магазина. Найдите вероятность того, что один из посетителей примет это предложение, а другой откажется.

7. Формула Байеса

При использовании формулы Байеса знаменатель выражения вычис-

ляется по формуле полной вероятности:

( ) = ∑ ( ) ( | ).

=1

Пример 16. В корзине три красных и семь зеленых яблок. Из корзины вынули одно яблоко и не глядя отложили в сторону. После этого из корзины достали еще одно яблоко, которое оказалось зеленым.

Найдите вероятность того, что яблоко, отложенное в сторону, также было зеленым.

Решение. События: 1 – «первое – зеленое», 2 – «первое – красное», – «второе – зеленое». Требуется найти ( 1| ). По формуле Байеса

( 1| ) = ( 1) ( | 1),( )

где вероятность ( ) находится по формуле полной вероятности:

26

( ) = ( 1) ( | 1) + ( 2) ( | 2).

Вероятности находим, используя классическое определение:

Пример 17. Проводится тестирование остаточных знаний по математике 10% вопросов проверяют знание линейной алгебры, 20% –

знание математического анализа, остальные – знание теории вероятностей. Студент считает, что вероятности того, что он не ответит на вопрос теста, составляет для указанных групп вопросов 0,01, 0,05 и 0,2 соответственно.

Получив очередной вопрос, студент даже не понял, к какому из трех разделов математики относится этот вопрос. Найдите вероятность того, что вопрос относится к теории вероятностей.

Решение. Введем обозначения. События: 1 – «вопрос по линейной алгебре», 2 – «вопрос по математическому анализу», 3 –

«вопрос по теории вероятностей». Студент не понял, к какому разделу относится вопрос, следовательно на вопрос не ответил. Событие – «на вопрос не ответил». Требуется найти ( 3| ).

В условии задачи заданы вероятности:

( 1) = 0,1; ( 2) = 0,2; ( 3) = 0,7;

27

( | 1) = 0,01; ( | 2) = 0,05; ( | 3) = 0,2.

По формуле полной вероятности:

( ) = ( 1) ( | 1) + ( 2) ( | 2) + ( 3) ( | 3) = = 0,1 ∙ 0,01 + 0,2 ∙ 0,05 + 0,7 ∙ 0,2 = 0,151.

Тогда по формуле Байеса:

( 3| ) = ( 3) ( | 3) = 0,7 ∙ 0,2 ≈ 0,927.( ) 0,151

Задачи для самостоятельного решения

31. Магазин получает однотипный товар от трех поставщиков: 55% товара поступает от первого поставщика, 20% от второго и 25% от третьего. Продукция, поступающая от первого поставщика, содержит

5% брака, поступающая от второго поставщика – 6% брака, поступа-

ющая от третьего поставщика – 8% брака. Покупатель оставил в книге пожеланий покупателей жалобу о неудовлетворительном качестве приобретенного товара. Найдите вероятность того, что плохой товар,

вызвавший нарекания покупателя, поступил от второго поставщика.

32. В пирамиде с винтовками одна винтовка снайперская и пять винтовок обычные. Стрелок случайным образом выбирает из пирамиды одну из шести винтовок, производит выстрел в мишень и попадает.

Определить, что более вероятно: произведен выстрел из обычной винтовки или со снайперской, если стрелок из обычной винтовки поражает мишень с вероятностью 0,6, а из снайперской – с вероят-

ностью 0,9.

28

33. Пассажир может обратиться за получением билета в одну из трех касс. Вероятность обращения в каждую кассу зависит от местоположения и равна соответственно 12 , 14 и 14. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равна: для первой кассы – 15, для второй – 12, для третьей – 13.

Пассажир направился за билетом в одну из касс и приобрел билет.

Найти вероятность того, что это была первая касса.

34. В некоторой страховой компании среди держателей полисов страхования автогражданской ответственности 20% относятся к группе высокого риска (у таких страхователей вероятность наступления страхового случая в течение года равна 0,1), а 80% − к группе низкого риска (у них вероятность наступления страхового случая в течение года равна 0,01). С какой вероятностью случайно выбранный страхователь, у

которого в прошлом году был страховой случай, относится к группе:

а) высокого риска; б) низкого риска?

35. Опыт отдела маркетинга фармацевтической фирмы показывает,

что после проведения рекламной кампании нового вида зубной пасты

5% мужчин и 10% женщин захотят приобрести новую пасту, а

остальные будут продолжать пользоваться прежними видами зубных паст. Число мужчин и число женщин в городе соотносятся как 2 3 и

все они покупают зубную пасту. Найдите вероятность того, что покупа-

тель, случайно отобранный среди купивших новый вид пасты, окажется женщиной.

29

8. Формула Бернулли

Предположим, что последовательно проводится некоторое число n

экспериментов (опытов, испытаний).

Если в каждом отдельном испытании может быть только два исхода: «успех» с вероятностью p или «неудача» с вероятностью = 1 − , то последовательность независимых испытаний называются схемой Бернулли (или биномиальной схемой испытаний).

Формула Бернулли позволяет вычислять вероятность того, что в n испытаниях успех произойдет заданное число раз k.

Вероятность того, что при n испытаниях, проводимых по схеме Бернулли, успех происходит ровно k раз, где k принимает значения

0, 1, … , , дается формулой Бернулли

Вычислить вероятность ( ) можно в Excel. Для этого нужно использовать функцию БИНОМ.РАСП(k; n; p; 0) (последний параметр всегда равен 0).

Функция Excel БИНОМ.РАСП(k; n; p; 1) (последний параметр ра-

вен 1) вычисляет вероятность того, что в n испытаниях успех произошел от 0 до k раз (включительно):

(0 ≤ ≤ ) = БИНОМ. РАСП( ; ; ; 1).

Если требуется найти вероятность того, что в n испытаниях успех произойдет от 1 до 2 (включительно), то отдельные вероятности нужно вычислять по формуле Бернулли, а затем все полученные значения сложить:

30