Physics

При отрицательном давлении жидкость как бы стягивает на себя стенки сосуда. Возникшее натяжение существует во всем объеме жидкости, а не только на ее поверхности.Жидкость остается сплошной средой благодаря действию сил когезии между молекулами жидкости и сил адгезии между молекулами жидкости и молекулами материала стенок сосуда.

Силы когезии довольно велики. Например, прочность воды на разрыв составляет !

3*10^7 Н/м2.

30. Характеристики течения. Поток жидкости и уравнение неразрывности.

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 8 расходы во входном и выходном сечениях трубы равны: q1=q2.

С учётом, что q=vω, получим уравнение неразрывности потока: v1ω1 = v2ω2 .

А если выразим скорость для выходного сечения v2 = v1ω1/ω2 ,

то можно заметить, что она увеличивается обратно пропорционально уменьшению площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.

31. Уравнение Бернулли.

Рассмотрим установившийся поток идеальной жидкости, которая является баротропной

средой (в таких средах давление зависит только от плотности, ). Пусть на жидкость действуют массовые силы консервативной природы (например, сила тяжести).

математически это означает, что существует потенциальная функция со свойством

, , .

В таких условиях уравнения Эйлера (2.15) допускают интеграл. преобразуем систему

(2.15б) посредством умножения каждого из уравнений соответственно на , и и почленного их сложения. Тем самым мы проецируем уравнения гидродинамики на линию тока. В левой части имеем

.

Справа получаем

,

где – функция давления. Таким образом,

либо . (2.17)

Это соотношение называют уравнением Бернулли в дифференциальной форме. Его следствием является интеграл Бернулли:

(вдоль линии тока). (2.18) Частные случаи

А) При движении несжимаемой жидкости в поле силы тяжести (, ,

)

. (2.19)

Б) Для адиабатического течения идеального газа [см. (2.16)]

. (2.20)

Соотношение (2.19) остается справедливым для любой линии тока, проходящей внутри струйки. Поэтому (2.19) можно назвать интегралом Бернулли для струйки идеальной жидкости. Для двух произвольных поперечных сечений струйки можно записать:

. (2.21)

Выясним физический смысл величин, входящих в интеграл Бернулли. Первые два члена

выражают удельную потенциальную энергию (положения и давления ), а третий – удельную кинетическую энергию. Следовательно, полная удельная энергия в любом сечении струйки остается неизменной. Другими словами, уравнение Бернулли выражает закон сохранения механической энергии.

В практических приложениях широко используется другая форма уравнения Бернулли –

форма напоров. Разделив обе части уравнения (2.21) на ускорение свободного падения , получим

. (2.22)

Каждый член (2.22) имеет линейную размерность и выражает напор, под которым в общем случае понимают высоту столба жидкости, уравновешивающего давление в данной точке.

Таким образом, – геометрический напор, характеризующий положение жидкой частицы над плоскостью отсчета; – пьезометрический напор, т. е. – высота столба

жидкости, уравновешивающего давление в данной точке; – скоростной напор. Сумма двух первых членов носит название гидростатического напора, а трех – полного

либо гидродинамического напора . Таким образом, интегралу Бернулли придается геометрическое толкование, которое сводится к следующему. Сумма трех высот:

геометрической (), пьезометрической () и скоростной () есть величина

постоянная вдоль струйки. Иными словами, полный напор 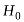при движении вдоль идеальной струйки остается неизменным.

32. Формула Пуазейля. Число Рейнольдса.

Течение вязкой жидкости по трубам представляет для медицины особый интерес, так как кровеносная система состоит в основном из цилиндрических сосудов разного диаметра. Вследствие симметрии ясно, что в трубе частицы текущей жидкости, равноудаленные от оси, имеют одинаковую скорость. Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; примыкающий к трубе слой жидкости неподвижен (Рис. 5).

Рис.5

Установим, от каких факторов зависит объем Q жидкости, протекающий через горизонтальную трубу за 1 с, или объемная скорость кровотока, или объемный расход крови:

Q = (2)

Эта зависимость носит название формулы Пуазейля, где η — вязкость жидкости, p1p2 — разность давлений, поддерживаемая на торцах трубы длиной l .Как видно из (2), при заданных внешних условиях (p1 и p2) через трубу протекает тем больший объем жидкости, чем меньше ее вязкость и больше радиус трубы.

Существует два характера течения жидкости: ламинарное (слоистое, установившееся, стационарное) и турбулентное ( вихревое, неустановившееся, нестационарное). Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы и определяется числом Рейнольдса:

, (5)

где - плотность жидкости, D – диаметр трубы.

Если число Рейнольдса больше некоторого критического ( Re>Re кр ), то движение жидкости турбулентное. Если число Рейнольдса меньше критического ( Re<Re кр ), то течение ламинарное.

Объясняя физический смысл числа Рейнольдса, следует обратить внимание на следующее:

а) когда Re<<1, мы можем сказать, что вязкие силы преобладают, а инерционные пренебрежимо малы. Например, на уровне микрососудов (сосуды диаметром порядка 100 мкм и менее) типичные числа Рейнольдса меньше единицы и течение можно рассматривать как чисто вязкое;

б) когда Re>>1, напротив, преобладают инерционные силы, а вязкость (во всех областях, кроме пограничных) лишь незначительно изменяет характер течения. Например, для крови в крупных артериях, в венах.

Так как число Рейнольдса зависит от вязкости и плотности жидкости, то удобно ввести их отношение, называемое кинематической вязкостью:

33. СТО. Вычисление релятивистской скорости, импульса и энергии.

Выражение, обеспечивающее инвариантность закона сохранения импульса, может быть получено, если вместо времени t подставить собственное время τ.

Тогда . Релятивистское выражение для энергии

В релятивистской механике справедливым остается выражение

.

Это означает, что . Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.

Легко получить выражение для кинетической энергии. Поскольку dEk = dA и dEk = v·p·dt, dA = F·ds

.

Отсюда следует, что E0 = mc2 является энергией покоя. Энергия и импульс в релятивистской механике не сохраняются. Инвариантом является выражение:

Взаимосвязь массы и энергии. Границы применимости механики Ньютона.

34. Элементарные сведения об электрических зарядах. Закон сохранения заряда. Закон взаимодействия точечных электрических зарядов на расстоянии (закон

Кулона).

Элемента́рный электри́ческий заря́д — фундаментальная физическая постоянная, минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц. Согласно изменениям определений основных единиц СИ равен точно 1,602 176 634 10−19 Кл в Международной системе единиц (СИ).

Один вид электрического заряда называют положительным, а другой — отрицательным. Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной: q1 + q2 + q3 + ... +qn = const.

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Зако́н Куло́на — экспериментальный физический закон, являющийся одним из основных законов электростатики, который описывает величину действующей между двумя электрически заряженными точечными частицами силы в состоянии покоя в вакууме. Эту электрическую силу условно называют электростатической или кулоновской силой. Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними

35. Объемная, поверхностная и линейная плотности заряда. Заряды как источники электростатического поля.

Плотность электрического заряда, скалярная физическая величина, равная величине электрического заряда, который приходится на единицу объёма (объёмная плотность электрического заряда), площади (поверхностная плотность электрического заряда) или длины (линейная плотность электрического заряда).

Объемная плотность заряда определяется, по аналогии с обычной плотностью, следующим образом:

где !q– заряд, заключенный внутри малого объема!V.

Кроме объемной плотности заряда нам понадобятся в дальнейшем

где !q– заряд, находящийся на элементе поверхности!S, и

где !q– заряд, находящийся на участке линии имеющем длину!l.

Электрические заряды являются источниками электрического поля. Характеризуется электрическое поле силой действия на заряженные частицы. Эта сила проявляется во взаимном притяжении или отталкивании зарядов.

36.Понятие математического векторного поля, источники поля и пробные заряды. Понятие напряженности электростатического поля. Силовые линии.

Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке.

Заряженные частицы — источники электрического поля. Электрическое поле действует на любой заряд, находящийся в поле. Напряжённость электрического поля убывает по мере отдаления от зарядов, которые это поле создают.

Пробный заряд, небольшой по величине точечный заряд, который не производит заметного перераспределения зарядов, создающих исследуемое поле. Величина пробного заряда должна быть настолько мала, чтобы он практически не приводил к перераспределению заряда на объектах, поле которых исследуется с его помощью. Напряженностью электростатического поля называется физическая величина, равная отношению силы, действующей со стороны поля на пробный заряд к величине этого заряда.

Силовая линия, или интегральная кривая — графическое средство для наглядного представления векторных полей. Изображается в виде кривой, касательная к которой в любой точке совпадает по направлению с вектором векторного поля в этой же точке.

37.Принцип суперпозиции (для электростатического поля). Понятие физического поля. Электростатическое поле как посредник, переносящий взаимодействие между зарядами через пространство.

Наиболее известен принцип суперпозиции в электростатике: напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть векторная сумма напряженности полей отдельных зарядов.

Область пространства, где проявляют себя физические, достоверно зарегистрированные и точно измеренные силы, называется физическим полем. В рамках современной физики рассматриваются четыре их вида: гравитационное (см. здесь); сильных взаимодействий (см. здесь) - ядерное; слабых взаимодействий (см. здесь) и электромагнитное (см. здесь) - магнитное и электрическое.

Основным свойством поля является то, что на находящуюся в этом поле заряженную частицу, действует некоторая сила, т. е. взаимодействие электрических зарядов

осуществляется посредством создаваемых ими полей. Поле, создаваемое неподвижными зарядами, не изменяется со временем и называется электростатическим.

38. Теорема Остроградского-Гаусса в вакууме. Применение теоремы ОстроградскогоГаусса для расчета полей простейших конфигураций.

Теорема Гаусса для напряжённости электрического поля в вакууме Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

Применение теоремы Остроградского-Гаусса для расчета электрического поля равномерно заряженной бесконечной плоскости.

Бесконечная плоская поверхность заряжена с постоянной поверхностной плотностью +σ

Линии напряженности направлены перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны.

В качестве замкнутой поверхности строим цилиндр с площадью основания S и с осью, перпендикулярной заряженной плоскости. Так как боковые поверхности цилиндра параллельны линиям напряженности, то поток вектора напряженности пересекает только основания цилиндра и равен 2ES.

По теореме Остроградского-Гаусса

→

Таким образом, напряженность поля не зависит от длины цилиндра. Из этого следует, что поле равномерно заряженной бесконечной плоскости однородно.

Применение теоремы Остроградского-Гаусса для расчета электрического поля равномерно заряженной бесконечной сферической поверхности.

Сферическая поверхность радиуса R с общим зарядом Q равномерно заряжена с постоянной поверхностной плотностью +σ. Поле обладает сферической симметрией и потому силовые линии направлены радиально.

Проведем мысленно сферу, радиуса r с центром, совпадающим с центром заряженной сферы.

При r>R внутрь поверхности попадает весь заряд Q. По теореме Остроградского-Гаусса

→

При r<R внутри мысленной поверхности заряда нет и, следовательно, поле отсутствует. Применение теоремы Остроградского-Гаусса для расчета электрического поля равномерно заряженного шара.

Шар радиуса R с общим зарядом Q равномерно заряжен с объемной плотностью +ρ

. Поле обладает сферической симметрией и потому силовые линии направлены радиально.

формулой для расчета работы по перемещению заряда q0 в однородном электростатическом поле

A=F l=q0E l. Приравнивая два выражения для работы, получим: q0(φ1−φ2)=q0E l E=φ1−φ2 l.

Модуль напряженности в любой точке поля численно равен разности потенциалов, приходящейся на единицу длины линии напряженности. Чем меньше l, тем теснее расположены эквипотенциальные поверхности, тем больше в этом месте напряженность поля.

В однородном поле l может быть любое. Если l = d, то

E=φ1−φ2d=−Δφd.

Эта формула выражает связь между напряженностью и разностью потенциалов однородного электростатического поля. На основании этой формулы можно установить единицу напряженности в СИ: вольт на метр (В/м).

40.Эквипотенциальные поверхности и их ортогональность силовым линиям. Принцип суперпозиции полей в применении к потенциалу.

Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение (поверхность уровня потенциала). Другое, эквивалентное, определение — поверхность, в любой своей точке ортогональная силовым линиям поля.

Для потенциалов справедлив принцип суперпозиции: если поле создается несколькими точечными зарядами, то потенциал любой его точке равен алгебраической сумме потенциалов (18.7), создаваемых в этой точке каждым точечным зарядом.

41.Примеры расчетов потенциалов полей простейших конфигураций.