Physics

1.Измерения, прямые и косвенные измерения. Понятие размерности физических величин.

Измерение физической величины – совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.

Прямые измерения производятся с помощью приборов, которые измеряют непосредственно саму исследуемую величину. Так, массу тела можно найти с помощью весов, длину измерить линейкой, а время — секундомером.

К косвенным относятся измерения таких физических величин, для нахождения которых необходимо использовать теоретическую связь с другими, полученными в прямых измерениях, величинами, например, нахождение объёма тела по его линейным размерам, нахождение плотности тела по

измеренным массе и объёму, расчёт сопротивления проводника по показаниям вольтметра и амперметра.

Размерность физической величины — количественная определенность физической величины, присущая конкретному материальному объекту, системе, явлению или процессу.

2.Элементы теории измерении (погрешность, методы статистических оценок и др.).

Погрешности физических измерений принято подразделять на систематические, случайные и грубые.

Систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Систематические погрешности скрыты в неточности самого инструмента и неучтенных факторах при разработке метода измерений. Обычно величина систематической погрешности прибора указывается в его техническом паспорте.

Что же касается метода измерений, то здесь все зависит от квалификации экспериментатора.

Случайные погрешности обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. Они имеют различные значения даже для измерений, выполненных одинаковым образом, то есть носят случайный характер.

Третий тип погрешностей, с которыми приходится иметь дело – грубые погрешности или промахи. Под грубой погрешностью измерения понимается погрешность, существенно превышающая ожидаемую при данных условиях. Она может быть сделана вследствие неправильного применения прибора, неверной записи показаний прибора, ошибочно прочитанного отсчета, не учета множителя шкалы и т.п.

В дальнейшем будем предполагать, что 1) грубые погрешности исключены;

2) поправки, которые следовало определить (например, смещение нулевого деления шкалы), вычислены и внесены в окончательные результаты; 3) все систематические погрешности известны (с точностью до знака).

Для оценки случайной погрешности измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратичной погрешности σ (ее часто называют стандартной погрешностью или стандартом измерений).

При ответственных измерениях, когда необходимо знать надежность полученных результатов, используется средняя квадратичная ошибка ! (или стандартное отклонение),

которая определяется формулой

(5)

Величина ! характеризует отклонение отдельного единичного измерения от истинного значения.

Если мы вычислили по n измерениям среднее значение по формуле (2), то это значение будет более точным, то есть будет меньше отличаться от истинного, чем каждое отдельное

измерение. Средняя квадратичная ошибка среднего значения равна

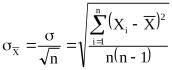(6)

где ! - среднеквадратичная ошибка каждого отдельного измерения, n – число измерений. Таким образом, увеличивая число опытов, можно уменьшить случайную ошибку в величине среднего значения.

В настоящее время результаты научных и технических измерений принято представлять в виде

(7)

Как показывает теория, при такой записи мы знаем надежность полученного результата, а именно, что истинная величина Х с вероятностью 68% отличается от не более, чем на

.

При использовании же средней арифметической (абсолютной) ошибки (формула 2) о надежности результата ничего сказать нельзя. Некоторое представление о точности проведенных измерений в этом случае дает относительная ошибка (формула 4).

При выполнении лабораторных работ студенты могут использовать как среднюю абсолютную ошибку, так и среднюю квадратичную. Какую из них применять указывается непосредственно в каждой конкретной работе (или указывается преподавателем). Обычно если число измерений не превышает 3 – 5, то можно использовать среднюю абсолютную ошибку. Если число измерений порядка 10 и более, то следует использовать более корректную оценку с помощью средней квадратичной ошибки среднего (формулы 5

и 6).

Увеличением числа измерений можно уменьшить только случайные ошибки опыта, но не систематические.

Максимальное значение систематической ошибки обычно указывается на приборе или в его паспорте. Для измерений с помощью обычной металлической линейки систематическая ошибка составляет не менее 0,5 мм; для измерений штангенциркулем –

0,1 – 0,05 мм; микрометром – 0,01 мм.

Часто в качестве систематической ошибки берется половина цены деления прибора. На шкалах электроизмерительных приборов указывается класс точности. Зная класс точности К, можно вычислить систематическую ошибку прибора ∆Х по формуле

где К – класс точности прибора, Хпр – предельное значение величины, которое может быть измерено по шкале прибора.

Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более

Среднее значение полной погрешности складывается из случайной и систематической погрешностей.

Ответ с учетом систематических и случайных ошибок записывается в виде

Погрешности косвенных измерений

В физических экспериментах чаще бывает так, что искомая физическая величина сама на опыте измерена быть не может, а является функцией других величин, измеряемых непосредственно. Например, чтобы определить объём цилиндра, надо измерить диаметр D и высоту h, а затем вычислить объем по формуле

Величины D и h будут измерены с некоторой ошибкой. Следовательно, вычисленная величина V получится также с некоторой ошибкой. Надо уметь выражать погрешность вычисленной величины через погрешности измеренных величин.

Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку.

Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.

Пусть искомая величина φ является функцией нескольких переменных Х, У, Z…

φ(Х, У, Z…).

Путем прямых измерений мы можем найти величины , а также оценить их средние

абсолютные ошибки … или средние квадратичные ошибки !Х, !У, !Z… Тогда средняя арифметическая погрешность !! вычисляется по формуле

где - частные производные от φ по Х, У, Z. Они вычисляются для средних

значений … Средняя квадратичная погрешность вычисляется по формуле

3. Понятие материальной точки. Системы отсчета. Принцип относительности Галилея.

Материальная точка — это абстрактный объект (модель), имеющий бесконечно малые размеры и обладающий некоторыми характеристиками реального тела. МТ применяется для анализа движения объектов, размерами которого можно пренебречь в условиях данной задачи. Такие объекты часто тоже называют «материальная точка», а иногда – «частица».

Положение МТ — это характеристика, определяющая расположение МТ относительно тел отсчета и соответствующей системы координат в данный момент времени. Математическое описание положения МТ — ее радиус-вектор r, проведенный из начала

координат, оси которой проходят через тела отсчета, в точку, где расположена МТ. Проекция радиус-вектора на оси системы координат называют координатами МТ. Система отсчета – совокупность системы координат и часов, связанных с телом по отношению к которому изучается движение.

Принцип относительности — фундаментальный физический принцип, один из принципов симметрии, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

4. Кинематика материальной точки.

Кинематика – раздел механики, в котором изучаются геометрические свойства движения тел без учета их массы и действующих на них сил.

Материальная точка — это абстрактный объект (модель), имеющий бесконечно малые размеры и обладающий некоторыми характеристиками реального тела. МТ применяется для анализа движения объектов, размерами которого можно пренебречь в условиях данной задачи. Такие объекты часто тоже называют «материальная точка», а иногда – «частица».

Положение МТ — это характеристика, определяющая расположение МТ относительно тел отсчета и соответствующей системы координат в данный момент времени. Математическое описание положения МТ — ее радиус-вектор r, проведенный из начала

координат, оси которой проходят через тела отсчета, в точку, где расположена МТ. Проекция радиус-вектора на оси системы координат называют координатами МТ. Механическое движение — есть изменение положения объекта в пространстве со временем.

Закон движения — это функция r(t) = {x(t), y(t), z(t)}, описывающая зависимость радиус-

вектора (координаты) от времени.

Скорость — есть векторная кинематическая характеристика движения, определяющая быстроту и направление движения.

Ускорение — есть векторная кинематическая характеристика движения, определяющая быстроту и направление изменения скорости.

Траектория — есть геометрическое место точек, которые проходит МТ при ее движении. В каждой точке вектор скорости направлен по касательной к траектории.

5.Динамика материальной точки. Понятие силы. Второй закон Ньютона.

4вопрос + Сила — физическая векторная величина, являющаяся мерой воздействия на данное тело

со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.

второй закон Ньютона: «Величина силы, действующая на тело, равна произведению массы тела на ускорение, которое получает тело, когда на него начинает действовать сила.»

6.Третий закон Ньютона.

Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

7. Закон всемирного тяготения. Инертная и гравитационная масса.

Закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Массу тела можно определить, используя второй закон Ньютона

Определяемая таким путем масса mин получила название инертной массы. Инертная масса является мерой инертности тела.

Массу того же самого тела можно определить, используя закон всемирного тяготения, путем измерения силы тяготения к другому телу, например к Земле:

Определяемая этим способом масса mграв носит название гравитационной массы. Гравитационная масса является, таким образом, количественной мерой присущему всем телам свойству гравитации.

8. Сила тяжести и вес.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору или подвес

На любое тело, расположенное вблизи Земли, действует сила тяготения F, под влиянием которой, согласно второму закону Ньютона, тело начнет двигаться с ускорением свободного падения g. Таким образом, в системе отсчета, связанной с Землей, на всякое тело массой m действует сила

P = mg,

называемая силой тяжести.

Согласно фундаментальному физическому закону — обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Так как различие значений g невелико, ускорение свободного падения, которое используется при решении практических задач, принимается равным 9,81 м/с2.

В физике применяется также понятие веса тела. Весом тела называют силу, с которой тело вследствие тяготения к Земле действует на опору (или подвес), удерживающую тело от свободного падения. Вес тела проявляется только в том случае, если тело движется с ускорением, отличным от g, т. е. когда на тело кроме силы тяжести действуют другие силы. Состояние тела, при котором оно движется только под действием силы тяжести, называется состоянием невесомости.

Таким образом, сила тяжести действует всегда, а вес появляется только в том случае, когда на тело кроме силы тяжести действуют еще другие силы, вследствие чего тело движется с ускорением а, отличным от g.

9. Работа. Кинетическая энергия.

Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения матери связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Механическая работа — физическая величина — скалярная количественная мера действия силы на тело или сил на систему тел. Зависит от численной величины и направления силы и от перемещения тела.

Кинетическая энергия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии.

10. Консервативные силы. Потенциальная энергия.

В физике консервативные силы — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки.

Потенциальная энергия U — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Потенциальная энергия зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении.

11. Сила трения. Диссипативные силы.

Трение — процесс механического взаимодействия соприкасающихся тел при их относительном смещении в плоскости касания либо при относительном смещении параллельных слоёв жидкости, газа или деформируемого твёрдого тела.

Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. Причиной возникновения трения является шероховатость трущихся поверхностей и взаимодействие молекул этих поверхностей.

Диссипативные силы — силы, при действии которых на механическую систему её полная механическая энергия убывает, переходя в другие, не механические формы энергии, например, в теплоту. Этим они отличаются от консервативных сил, под действием которых энергия системы сохраняется.

12. Закон сохранения энергии.

Полная механическая энергия — это сумма кинетической и потенциальной энергии тела. Полная механическая энергия системы тел остаётся неизменной, если тела взаимодействуют друг с другом силами тяжести и упругости.

Закон сохранения энергии: энергия не возникает и не исчезает, она может передаваться от одного тела к другому, а также один вид энергии может превращаться в другой.

13. Упругие столкновения. Закон сохранения импульса.

Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.

Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.

Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел Центральный удар – это соударение, когда скорости шаров направлены по линии центра.

Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид: m1v1=m1u1+m2u2.

14. Сила упругости. Энергия упругой деформации.

Сила упругости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное состояние. В случае упругих деформаций энергия деформации является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия Любое упруго деформированное тело обладает потенциальной энергией, так как

изменяется взаимное расположение отдельных частей тела. Рассмотрим случай растяжения пружины.

Растяжение будем производить очень медленно, чтобы силу , с которой мы действуем на пружину, можно было считать все время равной по модулю упругой силе

. Тогдагдек, х – соответственно жесткость и удлинение пружины. Тогда работа, которую нужно совершить, чтобы вызвать удлинение (или сокращение) х пружины, равна

(8.12)

Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид

, (8.13)

если считать, что потенциальная энергия недеформированной пружины равна нулю.

15. Динамика вращательного движения. Уравнение. Момент силы.

Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.

Возьмем однородную проволоку, верхний конец ее закрепим, а к нижнему концу приложим закручивающие силы. Они создадут вращающий момент относительно продольной оси проволоки. При этом каждый радиус нижнего основания повернется вокруг продольной

оси на угол . Такая деформация называется кручением. Закон Гука для деформации кручения имеет вид

, (8.15)

где – модуль кручения, постоянная для данной проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.

Выведем выражение для модуля кручения.

Пусть имеется цилиндрическая трубка радиуса . Причем толщина ееочень мала по

сравнению с радиусом. Площадь сечения трубки равна . Обозначим через касательное напряжение в том же основании. Тогда момент сил, действующий на это

основание, будет. При закручивании совершается работа

.

Разделим ее на объем трубки . Найдем плотность упругой энергии при деформации кручения

(8.16)

Найдем эту же величину иначе.

Мысленно вырежем из трубки бесконечно короткую часть (рис.8.5).

В результате кручения бесконечно малый элемент трубки ABDC перейдет в положение

. Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге равна

(8.17)

Приравнивая его выражению (8.16), находим искомое соотношение

(8.18)

Если стенка трубки имеет конечную толщину, то модуль найдется интегрированием

последнего выражения по. Это дает где – внутренний радиус трубки,

– внешний радиус трубки.

16. Момент инерции. Теорема Штайнера.

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

17. Момент импульса. Закон сохранения момента импульса.

Моментом импульса материальной точки, вращающейся относительно неподвижной оси OO′, называется величина L, равная произведению импульса этой точки на

расстояниеr от этой точки до оси вращения: .

Момент импульса является векторной величиной. Вектор направлен по оси вращения в соответствии с правилом правого винта.

При вращении твердого тела относительно неподвижной оси отдельные его точки,

находящиеся на различном расстоянии от оси вращения, имеют различные скорости

. Поэтому для того, чтобы найти момент импульса твердого тела относительно некоторой оси вращения, необходимо разбить это тело на элементарные объемы так, чтобы каждый элементарный объем можно было рассматривать как материальную точку

массой , находящуюся на расстоянииот оси вращения и движущаяся со скоростью

.

Тогда момент импульса твердого тела L равен сумме моментов импульса всех n

материальных точек массами , на которые разбито это тело:

.

Так как для твердого тела угловая скорость вращения всех материальных точек, на которые разбито это тело, одинакова, то, используя формулу, получим

или в векторной форме: .

Таким образом, момент импульса твердого тела относительно оси вращения равен произведению момента инерции этого тела относительно той же оси вращения на угловую скорость вращения этого тела.

Продифференцировав это уравнение по времени, получим:

, откуда . То есть

.

Это выражение – еще одна форма (называемая дифференциальной) уравнения динамики вращательного движения твердого тела: скорость изменения момента импульса твердого тела относительно оси вращения равна векторной сумме моментов всех действующих на это тело сил относительно той же оси вращения.

В замкнутой системе векторная сумма моментов внешних сил равна нулю. Тогда и,

следовательно,.

Таким образом, момент импульса замкнутой системы сохраняется, что является законом сохранения момента импульса.

18. Кинетическая энергия вращающегося тела. Работа внешней силы при вращении

Определим кинетическую энергию твёрдого тела, вращающегося вокруг неподвижной оси. Разобьем это тело на n материальных точек. Каждая точка движется с линейной

скоростью υi=ωri, тогда кинетическая энергия точки

или Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:

(3.22)

(J - момент инерции тела относительно оси вращения)

Если траектории всех точек лежат в параллельных плоскостях (как у цилиндра, скатывающегося с наклонной плоскости, каждая точка перемещается в своей плоскости

рис ), это плоское движение. В соответствии с принципом Эйлера плоское движение всегда можно бесчисленным количеством способов разложить на поступательное и вращательное движение. Если шарик падает или скользит вдоль наклонной плоскости, он двигается только поступательно; когда же шарик катится – он ещё и вращается.

Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна

(3.23)

Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что мерой инертности при вращательном движении служит момент инерции тела.

При вращении твёрдого тела его потенциальная энергия не изменяется, поэтому элементарная работа внешних сил равна приращению кинетической энергии тела:

dA = dE или

Учитывая, что Jβ = M, ωdr = dφ, имеем α тела на конечный угол φ равна

(3.25)

При вращении твёрдого тела вокруг неподвижной оси работа внешних сил определяется действием момента этих сил относительно данной оси. Если момент сил относительно оси равен нулю, то эти силы работы не производят.

19.Уравнение гармонического осциллятора. Энергия гармонического осциллятора.

Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида: s”+ω02s=0. Колебания гармонического осциллятора являются важным примером периодического движения, и служит точной или приближённой моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.

Свободными (собственными) колебаниями гармонического осциллятора называются колебания, которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния устойчивого равновесия; колебания, которые совершаются за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий на колебательную систему.

Энергия гармонического осциллятора.

Линейный гармонический осциллятор – материальная точка массой m, совершающая прямолинейные гармонические колебания под действием упругой силы. Уравнения движения осциллятора имеет вид md2x/dt2=-kx или d2x/dt2+kx/m=0. Где k – коэффициент, характеризующий упругие свойства пружины. Потенциальная энергия линейного гармонического осциллятора: Wп=kx2/2.

20.Математический маятник. Физический маятник.

Математический маятник — это материальная точка, подвешенная на невесомой и нерастяжимой нити, находящейся в поле тяжести Земли. Математический маятник — это идеализированная модель, правильно описывающая реальный маятник лишь при определенных условиях. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Колебательную систему в данном случае образуют нить, присоединенное к ней тело и Земля, без которой эта система не могла бы служить маятником.

,

где ах – ускорение, g – ускорение свободного падения, х - смещение, l – длина нити маятника.

Это уравнение называется уравнением свободных колебаний математического маятника. Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

1)будем считать, что силы трения, действующие на тело, пренебрежимо малы и потому, их можно не учитывать;

2)рассматриваются лишь малые колебания маятника с небольшим углом размаха. Свободные колебания любых систем во всех случаях описываются аналогичными уравнениями.

Причинами свободных колебаний математического маятника являются:

1. Действие на маятник силы натяжения и силы тяжести, препятствующей его смещению из положения равновесия и заставляющей его снова опускаться.

2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а проходит через него дальше. Период свободных колебаний математического маятника