Метод расчёта полнодоступных включений при обслуживании примитивного потока вызовов с потерями. Распределение Энгсета.
Используя информацию из методических
материалов, было рассчитано для заданного
числа
,
удельной интенсивности нагрузки
при
(поскольку для варианта 6 отсутствуют
значения был взят вариант 16) потери
,
,
,
они были сравнены по величине. Исходные
данные представлены в таблице 5.1.
Таблица 5.1 – Исходные данные из задания 1.
-
Эрл
0,3
8
16
Потери по вызовам (значение было взято из таблицы):
Потери по времени (значение было взято из таблицы):
Потери по нагрузке (формула 4.1)
Неравенство
выполняется, следовательно все значения
подобраны верно.
Построена зависимость числа линий
от интенсивности нагрузки для
фиксированного значения
,
где
при
.
Также была построена зависимость
количества линий
от нагрузки. Значения представлены в
таблице 5.2. График зависимости представлен
на рисунке 5.1.
Таблица 5.2 – Результаты расчётов числа линий.
-
№ п.п
,
Эрл
,
Эрл, Эрл
, Эрл
1
0,1
1
4
0,1
3
7
2
0,2
2
6
0,2
6
11
3
0,3
3
7
0,3
9
15
4
0,4
4
8
0,4
12
18
5
0,45
4,5
8
0,45
13,5
19
-
№ п.п
, Эрл
, Эрл
, Эрл
, Эрл
1
0,1
6
12
0,1
10
17
2
0,2
12
19
0,2
20
29
3
0,3
18
25
0,3
30
40
4
0,4
24
31
0,4
40
51
5
0,45
27
34
0,45
45
57
Рисунок 5.1 – Графики зависимости числа линий от нагрузки.
Были рассчитаны потери по нагрузке,
значение обслуженной нагрузки
и
.
Значения занесены в таблицу 5.3. Графики
зависимости коэффициента среднего
использования от нагрузки показан на
рисунке 5.2.
Таблица 5.3 – Результаты расчётов.
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0,098 |
0.024 |
4 |
0,024 |
1 |
0,097 |
0,014 |
7 |
0,031 |
3 |
|
0,197 |
0.033 |
6 |
0,016 |
2 |
0,195 |
0,018 |
11 |
0,025 |
6 |
|
0,296 |
0.043 |
7 |
0,012 |
3 |
0,294 |
0,02 |
15 |
0,020 |
9 |
|
0,397 |
0.05 |
8 |
0,008 |
4 |
0,394 |
0,022 |
18 |
0,016 |
12 |
|
0,446 |
0.056 |
8 |
0,008 |
4,5 |
0,443 |
0,023 |
19 |
0,015 |
13,5 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0,097 |
0.008 |
12 |
0,032 |
6 |
0,097 |
0,006 |
17 |
0,033 |
10 |
|
0,195 |
0.01 |
19 |
0,027 |
12 |
0,194 |
0,007 |
29 |
0,028 |
20 |
|
0,293 |
0.012 |
25 |
0,023 |
18 |
0,293 |
0,007 |
40 |
0,024 |
30 |
|
0,392 |
0.013 |
31 |
0,019 |
24 |
0,392 |
0,008 |
51 |
0,02 |
40 |
|
0,442 |
0.013 |
34 |
0,017 |
27 |
0,442 |
0,008 |
57 |
0,017 |
45 |
|
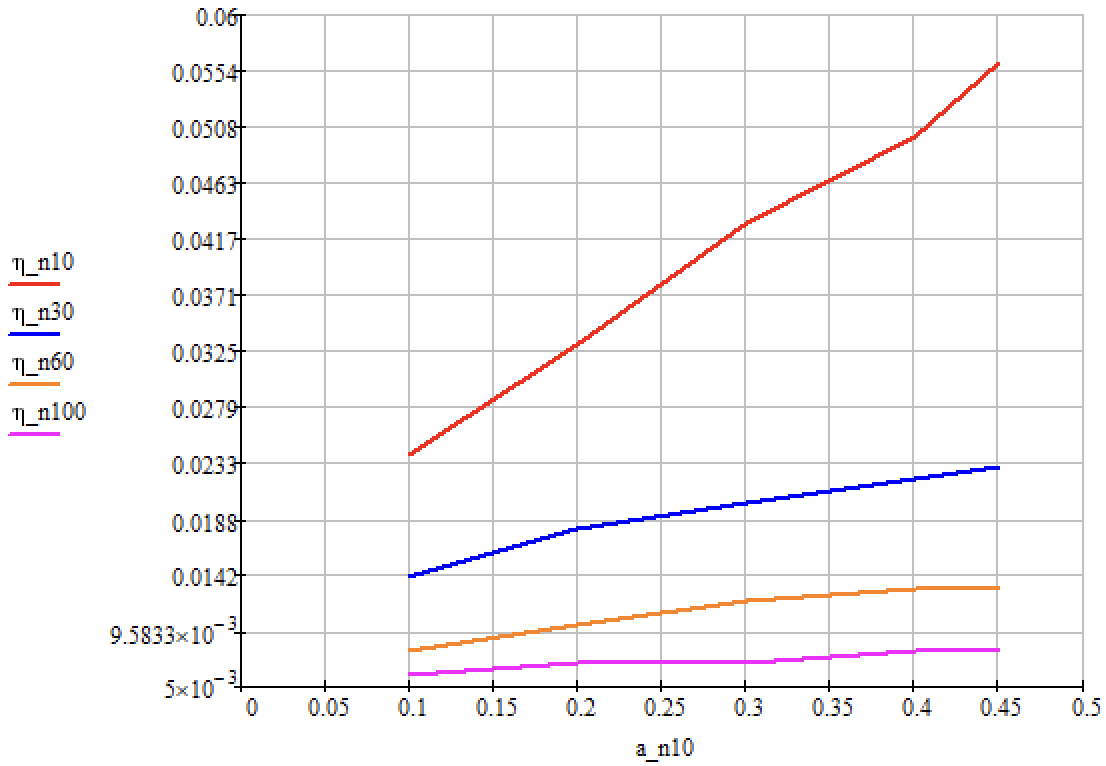
Рисунок 5.2 – Графики зависимости коэффициента среднего использования от нагрузки.