Филлипов, решение ряда задач / 1. Изоклины / 31

№31

Уравнение параболы, параллельной оси OY имеет вид

Уравнение касательной к параболе в точке

Поскольку парабола должна касаться прямой , то

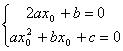
Выразим из первого уравнения  и подставим во второе уравнение:

Поскольку парабола должна касаться прямой

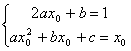
Выразим из первого уравнения  и подставим во второе уравнение:

Подставляем в это равенство ранее найденное соотношение , после приведения к общему знаменателю получаем

Откуда . Из соотношения  после подстановки   получаем

Таким образом, условиям задачи удовлетворяют семейство парабол

 (*)

Для составления дифференциального уравнения продифференцируем обе части равенства по х:

Откуда . Подставляя это значение в (*) получим

Ответ: