
Osnovy_teorii_inzhenernogo_experimenta_Uch_posobie_26_04_02
.pdf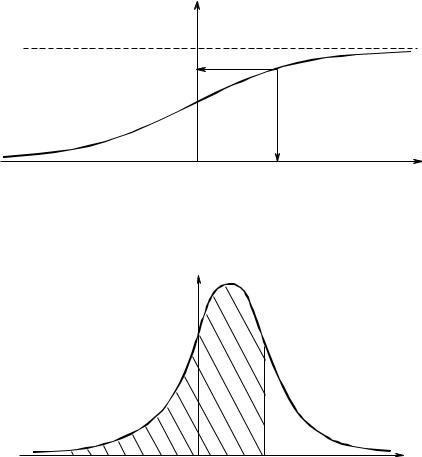
Функцию F(x) также называют интегральной функцией распределения.
Интегральная функция имеет один недостаток: по ней трудно судить о характере распределения непрерывной случайной величины в окрестно-
сти конкретной точки. Более наглядное представление о характере рас-
пределения непрерывной случайной величины даѐт функция p(x), назы-
ваемая плотностью распределения вероятностей непрерывной случай-
ной величины:
p(x) = F′(x).
Функцию p(x) иногда называют дифференциальной функцией распреде-
ления непрерывной случайной величины (рис. 1.2).
F |
|
|
1 |
|
|
F(x1) |
|
|
0 |
x1 |
x |
Рис. 1.1. Интегральная функция нормального распределения непрерывной случайной величины x
p |
|
|
|
F(x1) |
p(x) |
|
|
|
0 |
x1 |
x |
Рис. 1.2. Дифференциальная функция нормального распределения непрерывной случайной величины x
11
В теории эксперимента занимает центральное место и имеет наи-
важнейшее значение нормальное распределение (нормальный закон рас-
пределения или закон Гаусса). На рис. 1.1 схематично показана инте-
гральная функция нормального распределения, а на рис. 1.2 — диффе-
ренциальная функция нормального распределения.
Вероятность попадания случайной величины в определѐнный ин-
тервал значений равна площади под кривой p(x) между значениями ар-
гумента, ограничивающими это интервал. К примеру, вероятность того,
что случайная величина x попадѐт в интервал от –∞ до x1 равна
x1
P p(x)dx.
Применительно к распределению, подчиняющемуся нормальному зако-
ну (рис. 1.2), площадь, соответствующая указанному интегралу, заштри-
хована.
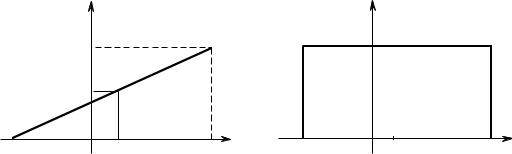
Помимо нормального распределения существует много других распределений случайных величин: равномерное (рис. 1.3), Пуассона,
показательное (рис. 1.4), Симпсона (треугольное) (рис. 1.5) и многие др.
а б
|
F(x) |
|
|
|
|
p(x) |
|
|
|
|
1,0 |
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
X1 |
0 |
Xмед |
X |
x |
X1 |
0 |
Xмед |
X |
x |
|
|
|
2 |
|
|
|
|
2 |
|
Рис. 1.3. Интегральная (а) и дифференциальная (б) функции равномерного распреде- |
|||||||||
|
|
|
|
|
ления |
|
|
|
|
Площадь под кривой плотности распределения p(x) равна единице.
Т. е. отражает вероятность появления всех возможных значений случай-
ной величины. Эту площадь можно разбить на части вертикальными ли-
12
ниями. Абсциссы таких линий называют квантилями. Квантили часто используют при описании непрерывных распределений.
|
а |
|
|
|
|
б |
F(x) |
|
|
p(x) |
|
|
|
|
|
|
|
|
|
|
1,0 |
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
0 |
Xмед |
x |
0 |
X |
мед |
x |
|
|
|
|
|
|
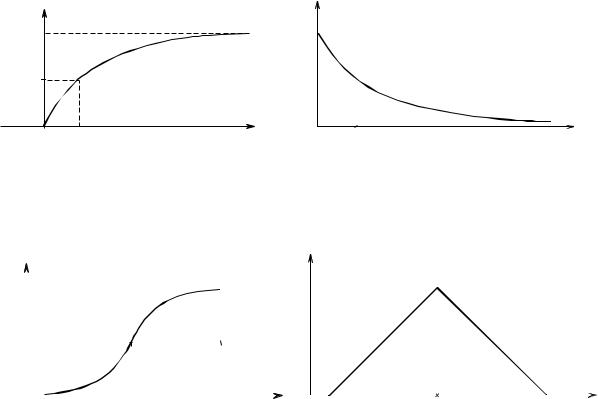
Рис. 1.4. Интегральная (а) и дифференциальная (б) функции показательного распределения
а б
F(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(x) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
X1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xмед= Xмод |
|
|
|
|
|
|
|
|
|
|
X |
x |
|
0 X |
Xмед= Xмод |
X |
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Рис. 1.5. Интегральная (а) и дифференциальная (б) функции о распределения Симпсона
Квантиль — это такое значение xP на оси абсцисс графика плотно-
сти распределения, при котором функция распределения принимает зна-
чение равное вероятности Р, т. е. F(xP) = Р. Иными словами, квантиль xP
— это значение абсциссы на графике p(x), соответствующее заданной вероятности Р.
Некоторые квантили имеют собственные названия. Так на рис. 1.6 x25 — 25 %-й квантиль, так как слева от него площадь под кривой p(x)
равна 25 % всей площади, а слева — 75 %. Соответственно x75 — 75 %-й
квантиль. 25%- и 75%-й квантили называют сгибами или квартилями.
13
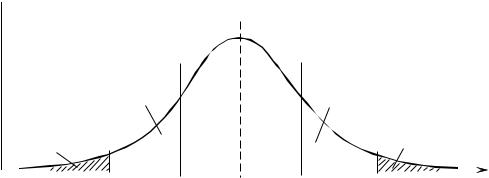
50%-й квантиль x50 называется медианой. Медиана — эта абсцисса на графики плотности распределения, которая делит площадь под кри-
вой p(x) на две равные части.
Мода распределения — это абсцисса, при которой плотность рас-
пределения p(x) достигает максимума. Не у всех распределений есть мо-
ду. Очень наглядно существование моды на нормальном (рис. 1.2) и тре-
угольном (рис. 1.5 б) распределениях. Для равномерного (рис. 1.3) и по-
казательного (рис. 1.4) распределений понятия моды не существует.
р(x) 
|
25 % |
25 % |
|
|
5 % |
5 % |
|
|
|
|
|
0 |
x5 x25 x50 |
x75 x95 |
x |
Рис. 1.6. Схема положения 5% -, 25% -, 50% -, 75% - и 95 % -ного квантилей на оси абсцисс
Для исследователя важно знать центр распределения, т. е. значе-
ние искомой случайной величины, вокруг которого группируется поле рассеяния значений случайной величины, и погрешность определения этого центра, т. е. ширину поля рассеяния.
Понятие центра распределения. Координата центра непрерывно-
го распределения определяется как медиана распределения.
Центр распределения может также быть определѐн по-иному, а
именно, как абсцисса центра тяжести площади под кривой распределе-
ния:
M x xp(x)dx. (1.1)
14

Центр распределения Mx, определѐнный по формуле (1.1), называ-
ется математическим ожиданием.
Следует помнить, что не для всех распределений центр тяжести может быть найден как математическое ожидание случайной величины,
так как интеграл (1.1) может расходиться (например, в случае распреде-
ления Коши1).
Оценка ширины распределения. Погрешность распределения.
Необходимо отметить, что распределения, имеющие чѐткие границы,
как например, равномерное (рис. 1.3) или треугольное (рис. 1.5) распре-
деление, являются скорее исключением, чем правилом. В большинстве случаев распределения плотности вероятности не имеют чѐтких границ
(рис. 1.2, 1.4), а поэтому указание для них предельных (максимальных и
(или) минимальных) границ рассеивания неправомерно. В подавляющем большинстве случаев в инженерной и научной практике используют
квантильные оценки погрешности.
Квантильная оценка погрешности — погрешность с заданной до-
верительной вероятностью Pд, т. е. с указанием границ интервала не-
определѐнности в пределах которого встречаются Pд процентов всех значений погрешности, а (1 – Pд) процентов от общего числа остаются за границами этого интервала.
Величина q = 1 – Pд называется уровнем значимости. Уровень зна-
чимости выражает вероятность того, что значение исследуемого пара-
метра не попадает в доверительный вариант. Иными словами значение q
показывает относительное количество результатов, погрешность кото-
рых значима (т. е. еѐ нельзя игнорировать, и учѐт результатов с такой погрешностью в зависимости от ситуации требует особого похода).
1 |
f (x) |
1 |
|
γ |
|
|
|
|
, где x0 |
и γ — параметры распределения, причѐм γ > 0. |
|
|
|
|
|
|
|
|
|||
|
π |
(x x0 ) |
2 |
γ |
2 |
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
15 |

Исторически сложилось так, что в разных областях знаний исполь-
зуют разные, традиционные для этих областей, значения доверительной вероятности: 50, 80, 90, 95, 99 %. Так например, если погрешность ре-
зультата указана с доверительной вероятностью Pд = 90 %, то 9 из 10
значений случайной величины попадут в интервал между 5%- и 95%-м
квантилями (рис. 1.6).
Для характеристики ширины полосы рассеяния (неопределѐнно-
сти) используется понятие среднего квадратического отклонения (СКО) σ случайной величины:
|
|
|
|
|
σ |
D |
(x M x )2 p(x)dx , |
||
|
|
|
|
|
где D — дисперсия, т. е второй центральный момент случайной величи-
ны.
СКО имеет такую же размерность, что и случайная величина и яв-
ляется нормированным показателем погрешности. Саму погрешность указывают в виде значений, кратных значению СКО, т. е. умножая на соответствующий квантильный коэффициент, зависящий от доверитель-
ной вероятности. Для нормального распределения:
погрешности равной значению 0,675σ соответствует Pд = 50 %,
погрешности равной значению σ соответствует Pд = 68 %,
погрешности равной значению 1,64σ соответствует Pд = 90 %,
погрешности равной 2σ соответствует Pд = 95 %,
погрешности равной 3σ соответствует Pд = 99,7 %.
Аналитическое описание нормального закона распределения.
Сприменением рассмотренных выше характеристик теоретического распределения дифференциальную функцию нормального закона рас-
пределения (рис. 1.2) можно записать следующим образом:
16

p |
1 |
|
|
(x М )2 |
|
|
|||
|
|
еxp |
|
|
x |
|
|
||
|
σ 2π |
|
|
2σ |
2 |
|
, |
(1.2) |
|
|
|
|
|
|
|
||||
где p — плотность распределения величины случайной величины x;
Мx — математическое ожидание; σ — СКО.
Кривая p(x) симметрична относительно значения x = Мx, и в этой точке функция имеет максимум:
p(М x ) |
|
1 |
|
. |
|
|
|
|
|
||
|
|
|
|
||
σ |
|
2π |
|||
|
|
|
|
||
Согласно выражению (1.2) интегральная функция нормального распределения (рис. 1.1) записывается в следующем виде:
|
x |
|
1 |
|
x |
( x M x )2 |
|
|
F(x) |
p(x)dx |
|
2σ2 |
|
||||
|
|
e |
dx. |
|||||
|
|
|
|
|||||
σ 2π |
|
|||||||
|
|
|
|
|
|
|
||
Сделаем следующую замену переменных: t = (x – Mx)/σ, тогда
|
1 |
|
|
|
t2 |
1 |
|
|
|
t2 |
|
|
|
|||||
|
|
t |
|
|
|
t |
|
x M |
|
|
||||||||
F(x) |
|
|
|
|
2 σdt |
|
|
|
|
2 dt Ф(t) Ф |
|
x |
|
|
||||
|
|
|
e |
|
|
|
|
e |
|
|
. |
(1.3) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
σ 2π |
|
|
|
|
|
2π |
|
|
|
|
σ |
|
|
|
|||
В выражении (1.3) функция Ф(t) — нормальная функция распреде-
ления. Для нормальной функции распределения в справочниках имеется таблица, в которой приводятся еѐ значения при разных значениях t.
Функцией Ф(t) удобно пользоваться для того, чтобы определить вероят-
ность попадания случайной величины x в интервал от x1 до x2; для этого необходимо рассчитать соответствующие значения t:
t1 = (x1 – Mx)/σ и t2 = (x2 – Mx)/σ.
Затем по таблице определить значения Ф(t1) и Ф(t2) и рассчитать вероят-
ность попадания случайной величины в интервал от x1 до x2 следующим образом:
P(t1 < x < t2) = Ф(t2) – Ф(t1).
17

1.3.2.Эмпирические распределения и их характеристики
Висследовательской и инженерной практике в большинстве слу-
чаев имеют дело с выборками, содержащими сравнительно небольшое количества значений случайной величины. А значит, работают с эмпи-
рическими распределениями случайной величины и, как следствие, с
выборочными оценками (или просто оценками, или статистиками) слу-
чайной величины.
Координату центра эмпирического распределения находят как оценку математического ожидания в виде среднего арифметического:
n
xi
x i 1 , (1.2) n
где xi — i-е значение случайной величины x, часто называемое вариан-
той; n — количество вариант (значений случайной величины) в выбор-
ке.
Варианта — это отдельное значение изучаемой случайной вели-
чины. Отбор вариант из генеральной совокупности должен происходить случайным образом, т. е. все варианты должны иметь одинаковую веро-
ятность попадания в выборку. Тем самым обеспечивают репрезента-
тивность выборки.
Репрезентативная выборка правильно представляет генеральную совокупность.
Преимущество использования в качестве оценки координаты цен-
тра распределения выражения (1.2) не в том, что это эффективная2
оценка, а в том, что эта единственная оценка, которую можно выразить аналитически, т. е. в виде формулы, и использовать эту в формулу в ма-
тематических выкладках.
Оценку СКО определяют по формуле:
2 Эффективная оценка — это оценка, обладающая среди прочих оценок того параметра наименьшей дисперсией.
18

|
n |
|
|
|
|
|
|
|
xi x 2 |
|
|||
S |
i 1 |
|
|
|
. |
(1.3) |
|
|
|||||
|
|
n 1 |
|
|||
Следует обратить внимание, что в знаменателе формулы (1.3) сто-
ит не n, а именно (n – 1). Это очень важно при работе с малыми выбор-
ками.
Значение (n – 1) в формуле (1.3), также как и значение n в формуле
(1.2) называют ещѐ числом степеней свободы.
Число степеней свободы v — это число независимых переменных
(вариант) минус количество наложенных связей (ограничений).
При вычислении среднего арифметического по формуле (1.2) ни-
каких ограничений ещѐ нет, т. е. v = n. При вычислении же оценки СКО имеется одно ограничение, так как значение СКО вычисляется по всем значениям вариант в выборке с использованием значения среднего арифметического. Но среднее арифметическое также рассчитывалось по всем значениям вариант в выборке. Это и будет ограничением. То есть одна степень свободы «израсходовалась» на определение среднего арифметического, а поэтому при вычислении СКО единица вычитается из числа n, тем самым оценка СКО получается несмещѐнной3.
Для определения оценок математического ожидания и СКО не требуется какого-либо группирования экспериментальных данных. Од-
нако для определения медианы, сгибов, других квантилей, для обнару-
жения промахов и т. п. необходимо произвести ранжирование.
Ранжирование — это расположение всех имеющихся вариант в выборке в порядке возрастания или убывания.
Для определения формы распределения, сопоставления гипотез о форме распределения и определения более сложных характеристик рас-
пределения простого ранжирования уже недостаточно: необходимо по-
3 Оценка параметра называется несмещѐнной, если при любом числе наблюдений n еѐ математическое ожидание точно равно значению оцениваемого параметра.
19
строить ряд распределения (вариационный ряд) и представить выборку графически в виде гистограммы распределения частот. Для непрерыв-
ной случайной величины для этого предварительно строится интерваль-
ный вариационный ряд Интервальный вариационный ряд — двойной ряд чисел, в первом
ряду которого указаны интервалы изменения случайной величины (в по-
рядке возрастания), а во втором — частоты появления значений случай-
ной величины из каждого интервала.
Например, интервальный вариационный ряд распределения твѐр-
дости стали может выглядеть следующим образом:
Таблица 1.1 Построение интервального вариационного ряда по результатам измерения твѐрдо-
сти
Твѐрдость HRC |
22–24 |
24–26 |
26–28 |
28–30 |
30–32 |
Частота fi (число) появления ре- |
5 |
32 |
40 |
20 |
8 |
зультатов в интервале |
|
|
|
|
|
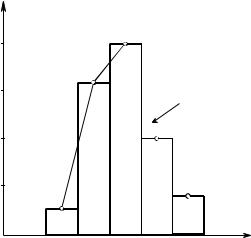
На основании полученного интервального вариационного ряда строят гистограмму (распределения частот). При построении гистограм-
мы по оси абсцисс откладывают интервалы значений случайной величи-
ны, а по оси ординат — частоты fi (рис. 1.7).
fi
40 |
|
|
|
|
|
30 |
|
|
|
Полигон |
|
20 |
|
|
|
|
|
10 |
|
|
|
|
|
0 |
24 |
26 |
|
30 |
32 HRC |
22 |
28 |
||||
Рис. 1.7. Гистограмма и полигон распределения частот, построенные на основании интервального вариационного ряда в табл. 1.1
20
