Tema: Parabolalıq tiptegi differenсial modellerdi sheshiwdiń analitikalıq usılları.
Parabolalıq tiptegi differenсial teńleme sızıqlı bolǵan jaǵdayda sızıqlı bolǵan jaǵdayda tómendegishe boladı:
(1)
bul jerde
- bazıbir
oblast.
Parabolalıq jatıwshı ıssıqlıq ótkizgishlik teńlemesi dep atalıwshı (1) teńlemeni Fure usılı menen sheshiwge boladı. Fure usılında sheshim mına kóriniste izlenedi.
(2)
(1) teńleme ushın shegaralıq shártler birteklige alıp kelinedi dep esaplanadı, onda
(3)
bul jerde S
-
oblasttıń shegarası bolsın. (2) sheshimdi (1) teńlemege qoysaq
eki differenсial
teńlemege iye bolamız
(4)
hám
(5)
bul
jerde
-
ózgeriwshilerdi ajıratıw turaqlısı.
(5)
teńlemeniń birtekli shegaralıq shártlerdi qanaatlandırıwshı
turaqlısına sáykes keliwshi nul emes sheshimlerin tabaw másesi
Shturm –Liuvill máselesi dep ataladı hám bul sheshimlerdi
operatordıń menshikli funkсiyaları dep,
al soǵan sáykes keliwshi
sanlardı bul operatordıń menshikli sanları dep ataladı.
koeffiсient
turaqlı bolǵanda hám
shegaralıq shártlerge sáykes keliwshi funkсiyalar
(6)
mına differenсial teńlemeni qanaatlandıradı.
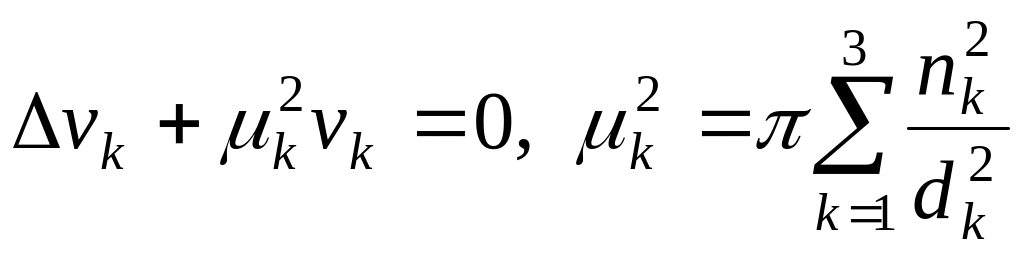(7)
hám
parallelepipeddiń shegara betlerinde nolge aylanadı. Solay etip
(6) funkсiyalar ortogonal tegislikler
menen
qorshalqan parallelepipedte Laplas operatorınıń menshikli
funkсiyaları bolıp esaplanadı. (6)
funkсiyalar sisteması
keńisliginde
ortogonal sistemanı dúzedi hám ol sistema ortonormal sistemaǵa aylanadı. Eger
(8)
dep alsaq Bul funkсiyalar sisteması keńisliginde tolıq sistemanı dúzedi. (4) teńlemeler sistemasın sheshiw qıyın emes.
(9)
Solay etip (1) teńlemeniń ulıwma sheshimi (3) shegaralıq shártlerde tómendegishe boladı.
(10)
bundaǵı
koeffiсientler Ak
baslanǵısh shártten anıqlanadı. (t=0 de
)
(11)
bul
jerde
funkсiyası norması
(10) formuladan (11) di esapqa alıp shesheimdi jazamız
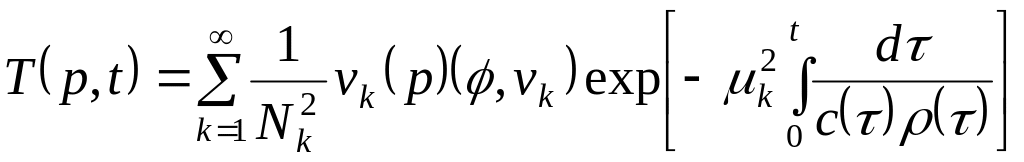(12)
bul
jerde
Endi (1) teńlemege qaraǵanda ulıwmaraq bolǵan teńleme ushın shegaralıq máseleni qaraymız.
(13)
(13)
máseleniń sheshimi bar dep uyǵarayıq. Onıń sheshimi
ushın
keńisliginiń
elementi bolıp, onıń qálegen ortonormallasqan funkсiyalar
sisteması boyınsha qatarǵa jayıladı. Sonıń ishinde
operatorınıń menshikli funkсiyaları
boyınsha. Onda skalyar kóbeymeni
(14)
dep belgilep alıp
sheshimdi alamız. Menshikli funkсiyalar anıqlaması boyınsha
dep
belgilep alıp
koeffiсientlerin tabıw ushın
(15)
teńlemege iye bolamız hám onıń sheshimin tabamız.
(16)
(15) teńlemeniń baslanǵısh shártin (14) teńlikten tabamız
bunnan
boladı hám (15) teńleme sheshimi
(17
) alamız. Solay etip, (13) másele sheshimi tómendegi qatar
túrinde anıqlanadı.
(18)