
Лабы (Семин) / МЛИТА6 Вариант 2
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Информатика»
Лабораторная работа №6
по дисциплине
«Математическая логика и теория алгоритмов»
на тему «Основы нечеткой логики»
Вариант 2 (№ 4, 10, 9).
Выполнил:
студент гр. БББ0000
Фамилия И.О.
Проверил:
Сёмин В.Г.
Задание 1. Нахождение основных характеристик нечеткого множества.
Для заданного дискретного нечеткого множества А найти носитель, ядро, высоту, мощность, множества уровня (для заданных значений α). Указать, является ли данное множество нормальным. Если является субнормальным, преобразовать его к нормальному. Проверить является ли нормализованное множество унимодальным.
-
Вариант
А
α
4
{0,1/-2; 0,3/-1; 0,9/0; 1/1; 1/2; 0,8/3; 0,5/4}
0,5
0,7
Заданное дискретное нечеткое множество: A {µA(x) / x} A = {0,1/-2; 0,3/-1; 0,9/0; 1/1; 1/2; 0,8/3; 0,5/4}; α1=0,5; α2=0,7.
Носителем нечеткого подмножества А называется четкое подмножество из Х, на котором µA(x)>0.
σ(x) = { х / µA(x)>0} = {-2; -1; 0; 1; 2; 3; 4} – носитель.
Ядром нечеткого подмножества А называется множество его элементов, для которых μA(х) = 1.
Core(A) = {1; 2} – ядро.
Высотой d нечеткого множества A называется максимальное значение функции принадлежности этого множества. d = max µA(x) = 1 – высота.
![]() =
0,1+0,3+0,9+1+1+0,8+0,5 = 4,6
– мощность.
=
0,1+0,3+0,9+1+1+0,8+0,5 = 4,6
– мощность.
Множеством - α уровня является множество элементов универсального множества, степень принадлежности которых нечеткому множеству ≥ α.
A0,5 = {x/ µA(x) ≥ 0,5} = {0; 1; 2; 3; 4} – множество уровня для α1=0,5;
A0,7 = {x/ µA(x) ≥ 0,7} = {0; 1; 2; 3} – множество уровня для α2=0,7.
Высота d = 1, следовательно, нечеткое множество является нормальным.
Нечёткое
множество не
является унимодальным
(так
как нечёткое множество унимодально,
если
![]() только на одном х из Е).
только на одном х из Е).
Задание 2. Операции над нечеткими множествами.
Дано 3 нечетких множества A, B, C (заданы их функции принадлежности). Построить функцию принадлежности нечеткого множества D.
М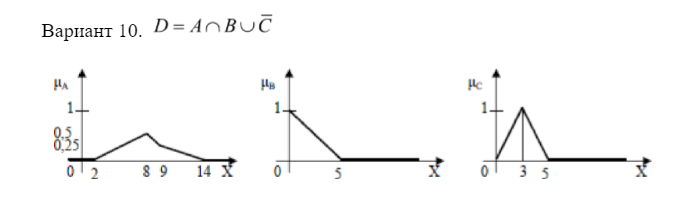 ножество:
D
=
ножество:
D
=
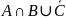
Последовательность
операций:
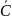 ,
,
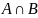 ,
.
,
.
 Функция
принадлежности
:
Функция
принадлежности
:
(Дополнение:
C
и
дополняют друг друга, если
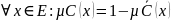 )
)
Функция принадлежности :

(Пересечение:
A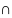 B–
наибольшее нечёткое подмножество,
содержащееся одновременно в A и B )
B–
наибольшее нечёткое подмножество,
содержащееся одновременно в A и B )
Функция принадлежности :
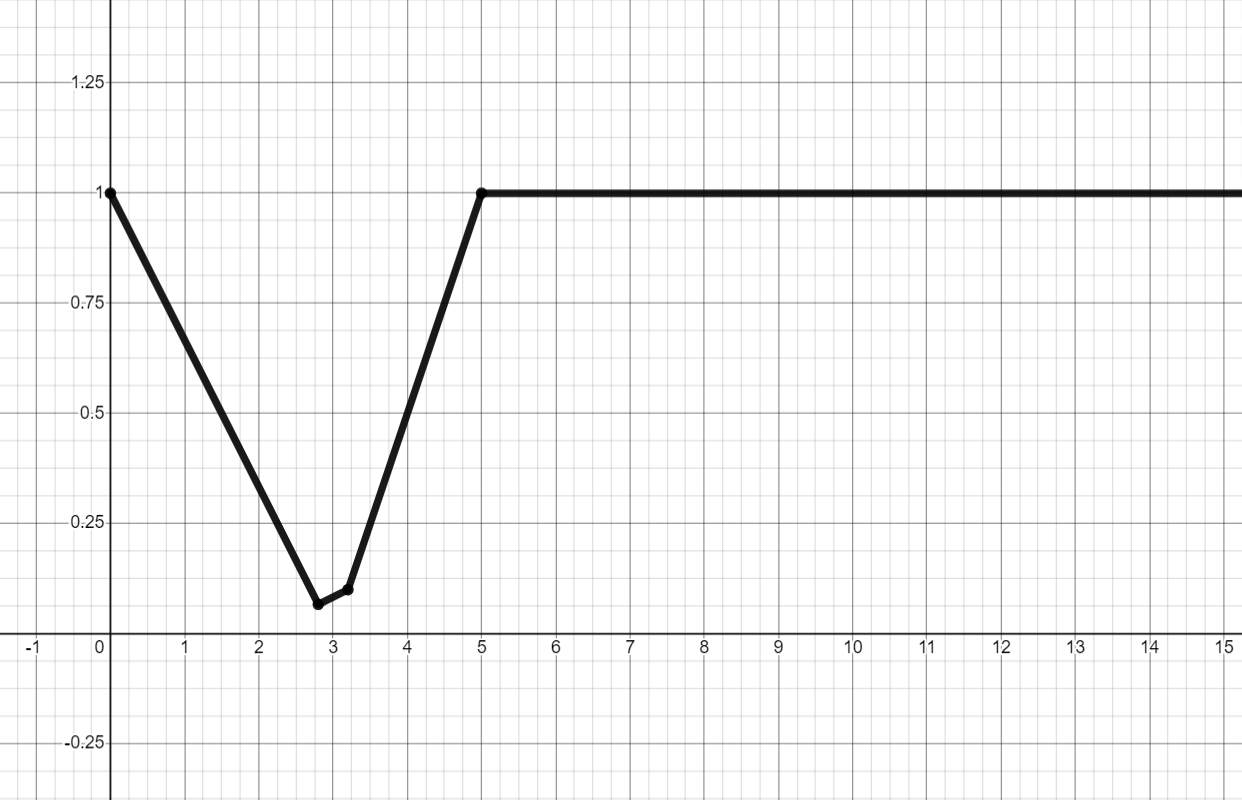
(Объединение:
 –
наименьшее нечёткое подмножество,
включающее как
,
так и
)
–
наименьшее нечёткое подмножество,
включающее как
,
так и
)
Задание 3. Нечеткие множества А, В и С заданы таблично. Вычислить значение выражений.
№ 9 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
х7 |
x8 |
A |
0,9 |
0,8 |
0.5 |
0.4 |
0,3 |
0,3 |
0,2 |
0 |
B |
0,3 |
0,5 |
0,4 |
0,2 |
0,1 |
0,1 |
0,5 |
0,7 |
C |
0,1 |
0,7 |
1 |
0,4 |
0,3 |
0,2 |
0,9 |
0 |
(B∩C)+A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = 0.9/x1+0.8/x2+0.5/x3+0.4/x4+0.3/x5+0.3/x6+0.2/x7+0/x8
B = 0.3/x1+0.5/x2+0.4/x3+0.2/x4+0.1/x5+0.1/x6+0.5/x7+0.7/x8
C = 0.1/x1+0.7/x2+1/x3+0.4/x4+0.3/x5+0.2/x6+0.9/x7+0/x8
(B∩C)
=(![]() )=
0.1/x1+0.5/x2+0.4/x3+0.2/x4+0.1/x5+0.1/x6+0.5/x7+0/x8
)=
0.1/x1+0.5/x2+0.4/x3+0.2/x4+0.1/x5+0.1/x6+0.5/x7+0/x8
(B∩C)+A =
(![]() )
=
=
(0.1+0.9-0.1*0.9)/x1+(0.5+0.8-0.5*0.8)/x2+(0.4+0.5-0.4*0.5)/x3+
(0.2+0.4-0.2*0.4)/x4 +
+
(0.1+0.3-0.1*0.3)/x5+(0.1+0.3-0.1*0.3)/x6+(0.5+0.2-0.5*0.2)/x7+(0+0-0*0)/x8
=
=
0.91/x1+0.9/x2+0.7/x3+0.52/x4+0.37/x5+0.37/x6+0.6/x7+0/x8
)
=
=
(0.1+0.9-0.1*0.9)/x1+(0.5+0.8-0.5*0.8)/x2+(0.4+0.5-0.4*0.5)/x3+
(0.2+0.4-0.2*0.4)/x4 +
+
(0.1+0.3-0.1*0.3)/x5+(0.1+0.3-0.1*0.3)/x6+(0.5+0.2-0.5*0.2)/x7+(0+0-0*0)/x8
=
=
0.91/x1+0.9/x2+0.7/x3+0.52/x4+0.37/x5+0.37/x6+0.6/x7+0/x8
(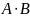 )
= (
)
= (![]() )
=
(0.9*0.3)/x1+(0.8*0.5)/x2+(0.5*0.4)/x3+(0.4*0.2)/x4+
+(0.3*0.1)/x5+(0.3*0.1)/x6+(0.2*0.5)/x7+(0*0.7)/x8
=
= 0.27/x1+0.4/x2+0.2/x3+0.08/x4+0.03/x5+0.03/x6+0.1/x7+0/x8
)
=
(0.9*0.3)/x1+(0.8*0.5)/x2+(0.5*0.4)/x3+(0.4*0.2)/x4+
+(0.3*0.1)/x5+(0.3*0.1)/x6+(0.2*0.5)/x7+(0*0.7)/x8
=
= 0.27/x1+0.4/x2+0.2/x3+0.08/x4+0.03/x5+0.03/x6+0.1/x7+0/x8
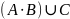 =
(
=
(![]() )
=
= 0.27/x1+0.7/x2+1/x3+0.4/x4+0.3/x5+0.2/x6+0.9/x7+0/x8
)
=
= 0.27/x1+0.7/x2+1/x3+0.4/x4+0.3/x5+0.2/x6+0.9/x7+0/x8
Результат:
№ 9 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
х7 |
x8 |
A |
0,9 |
0,8 |
0.5 |
0.4 |
0,3 |
0,3 |
0,2 |
0 |
B |
0,3 |
0,5 |
0,4 |
0,2 |
0,1 |
0,1 |
0,5 |
0,7 |
C |
0,1 |
0,7 |
1 |
0,4 |
0,3 |
0,2 |
0,9 |
0 |
(B∩C)+A |
0.91 |
0.9 |
0.7 |
0.52 |
0.37 |
0.37 |
0.6 |
0 |
|
0.27 |
0.7 |
1 |
0.4 |
0.3 |
0.2 |
0.9 |
0 |
Теоретические вопросы:
Что такое характеристическая функция обычного множества и функция принадлежности нечеткого множества.
Характеристическая функция обычного множества – это функция принадлежности элемента множеству, которая может принимать значение 1, если элемент удовлетворяет свойству, и 0 – в противном случае.
Функция
принадлежности нечеткого множества
(![]() )
– функция, принимающая значения в
некотором упорядоченном множестве М
(например, М=[0,1]), которая указывает
степень (или уровень) принадлежности
элемента х подмножеству А.
)
– функция, принимающая значения в
некотором упорядоченном множестве М
(например, М=[0,1]), которая указывает
степень (или уровень) принадлежности
элемента х подмножеству А.
Дайте определение операции пересечения нечетких множеств.
Пересечение
A
B
– наибольшее нечёткое подмножество,
содержащееся одновременно в A и B:
![]()
Москва, 2023
