Otvety_na_kontrolnye_voprosy_GEODEZIYa

Ответы на контрольные вопросы

Лекция№1

1.1Основы геодезии

1.Когда и кем впервые были высказаны предположения о шарообразности Земли?

Идея шарообразности Земли возникла еще у древних греков: Пифагор (IV в. до н. э.), Парменид (IV

– V вв. до н. э.), Аристотель (IV в. до н. э.).

Но потом эта идея оставалась в забвении более полутора тысяч лет, до времен Колумба и кругосветных путешествий.

2. Какая поверхность называется уровенной поверхностью?

Поверхность сложной формы, в каждой точке которой линия направления силы тяжести совпадает с нормалью к этой поверхности, называется уровенной поверхностью.

3. Что такое геоид?

Геоид – теоретическая фигура Земли, ограниченная уровенной поверхностью, которая совпадает с поверхностью морей и океанов в невозмущенном состоянии и мысленно продолженная под материками и континентами таким образом, чтобы в каждой точке этой поверхности отвесная линия была перпендикулярна ей.

4. Что такое эллипсоид вращения?

Эллипсоид вращения – это поверхность, образующаяся путём вращения эллипса вокруг его малой полуоси.

5. Что такое коэффициент сжатия? Записать формулу для определения сжатия.

Сжатие – разность в длине между двумя осями, выраженная простой или десятичной дробью:

a − b= a

Сжатие является маленькой величиной, поэтому как правило вместо него используется величина

1/f.

6. Что такое референс-эллипсоид?

Референц–эллипсоидом называется эллипсоид вращения с определенными размерами его полуосей, определенным образом ориентированный в теле Земли и принятый для геодезических работ в данной стране.

7. Параметры эллипсоида Крассовского?

Эллипсоид Красовского (1940) (Большая полуось, 6378245 м; Сжатие, 1:298,3)

Параметры эллипсоида (Красовского) наиболее подходящие для территории нашей страны:

а = 6 378 245 м b = 6 356 863 м, α = 1:298,3. (Радиус сферы R = 6371,11 км.)

8. Параметры эллипсоида Вашей страны?

Эллипсоид Красовского (1940) (Большая полуось, 6378245 м; Сжатие, 1:298,3)

Параметры эллипсоида (Красовского) наиболее подходящие для территории нашей страны:

а = 6 378 245 м b = 6 356 863 м, α = 1:298,3. (Радиус сферы R = 6371,11 км.)

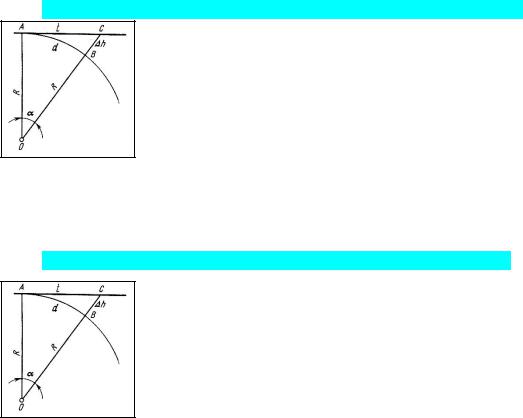
9. Влияет ли кривизна Земли на определение горизонтальных расстояний?

Докажем, что малый участок поверхности Земли - плоскость, и тогда можем пренебречь влиянием кривизны Земли на горизонтальные расстояния. Возьмем плоскость, касательную в точке А, и продолжим радиус ОВ до пересечения с этой плоскостью в точке С. Если участок сферы, соответствующий дуге d, принять за плоскость, соответствующую отрезку касательной АС=t, то допустим ошибку в горизонтальном расстоянии, равную

d = t – d.

(Влияние кривизны Земли на определение горизонтальных расстояний при l=10 км

составляет 1: 1 200 000 ее длины, что допустимо при самых точных измерениях горизонтальных расстояний на земной поверхности).

10. Влияет ли кривизна Земли на определение вертикальных расстояний? Для вертикального расстояния ошибка составит h = OC – OВ.

Учтя, что d весьма незначительно по сравнению с R, можно рассчитать относительные ошибки и значения ошибок d в горизонтальных расстояниях и h в вертикальных расстояниях (в превышениях).

(Кривизна Земли оказывает значительное влияние на определение вертикальных расстояний).

Лекция№2

1.2Изображение земной поверхности на плоскости

1.Что такое картографическая проекция?

Картографическая проекция – представление трёхмерной сферической поверхности планеты на двумерной плоскости карты.

2.Классификация картографических проекций?

3.Классификация картографических проекций по характеру искажений? По характеру искажений картографические проекции делятся на три группы:

▪ равновеликие проекции, передающие без искажений площади любых фигур на эллипсоиде

икарте;

▪равноугольные или конформные проекции, сохраняющие углы и направления при передаче их с эллипсоида на карту. В них сохраняется подобие малых фигур. В то же время линейные размеры фигур на этих проекциях искажены. Поэтому два одинаковых по форме и размерам участка земли, но лежащие на разной широте, изобразятся на карте подобными по форме контурами, но с различными размерами;

▪произвольные проекции, не сохраняющие ни равенства углов, ни пропорциональности площадей. Примером этой проекции является равнопромежуточная проекция, в которой сохраняется масштаб изображения по одному из направлений (меридианам или параллелям).

4. Классификация картографических проекций по способу ориентирования?

По способу ориентирования вспомогательных геометрических поверхностей картографические проекции делятся на три группы:

▪полярные (нормальные), в которых плоскость проектирования касается поверхности земного шара в точке полюса, или ось цилиндра (или конуса) совпадает с осью вращения Земли;

▪экваториальные (поперечные), в которых плоскость проектирования касается экватора в какой-либо точке, или ось цилиндра (или конуса) совпадает с плоскостью экватора;

▪Косые (горизонтальные), в которых плоскость проектирования касается земного шара в любой заданной точке.

5. Классификация картографических проекций по виду меридианов и параллелей?

По виду меридианов и параллелей нормальной сетки различают следующие картографические проекции:

▪цилиндрические, в которых меридианы изображены равноотстоящими параллельными прямыми, а параллели - прямыми, перпендикулярными к ним;

▪конические, с прямыми меридианами, исходящими из одной точки, и параллелями, представленными дугами концентрических окружностей;

▪азимутальные, в которых параллели изображаются концентрическими окружностями, а меридианы - радиусами, проведенными из общего центра этих окружностей;

▪псевдоцилиндрические, где параллели представлены параллельными прямыми, а меридианы - в виде кривых, увеличивающих свою кривизну по мере удаления от прямого центрального меридиана;

▪псевдоконические, в которых параллели представлены дугами концентрических окружностей, средний меридиан − прямой, а остальные меридианы − кривыми;

▪поликонические, в которых параллели изображены эксцентрическими окружностями, центры которых лежат на прямом центральном меридиане, а остальные меридианы − кривыми линиями, увеличивающими кривизну с удалением от центрального меридиана;

▪псевдоазимутальные, в которых параллели представляют концентрические окружности, а меридианы − кривые линии, симметричные относительно одного или двух прямых меридианов;

▪условные, для которых нельзя подобрать геометрические аналоги. Их строят, исходя из заданных условий (например, вида географической сетки или преобразования одной или нескольких сходных проекций.

6. Характеристики проекций Ламберта, Руссиля, Меркатора?

7.Основные свойства проекции Гаусса-Крюгера? Основные свойства проекции Гаусса-Крюгера:

▪ осевой меридиан зоны изображается без искажений; ▪ проекции осевого меридиана и экватора являются прямыми линиями, перпендикулярными

друг к другу; ▪ в проекции обеспечивается сохранение подобия малых фигур;

▪ в проекции обеспечивается сохранение горизонтальных углов и направлений на

изображении и местности; ▪ масштаб изображения на осевом меридиане равен единице, т. е. для точек осевого

меридиана абсциссы равны дугам меридиана, отсчитанным от экватора

8.Что такое осевой меридиан зоны?

9.Как вычислить долготу осевого меридиана зоны в восточном полушарии? Формула.

10.Как вычислить долготу осевого меридиана зоны в западном полушарии? Формула.

Лекция№3

1.3Системы координат

1.Какими величинами характеризуется геодезическая система координат?

2.Какими величинами характеризуется географическая система координат?

3.Дать определение геодезической широты и долготы.

4.Дать определение географической широты и долготы.

5.Дать понятие полярной системы координат. Какими величинами характеризуется полярная система координат?

6.Записать формулы связи полярных и прямоугольных координат.

7.Какие высоты называются абсолютными, относительными?

8.Дать понятие зональной прямоугольной системы координат Гаусса.

9.Написать условное значение ординаты, расположенной в 5 зоне к западу от осевого меридиана на расстоянии 96422,5 м.

10.Написать условное значение ординаты, расположенной в 6 зоне к востоку от осевого меридиана на расстоянии 153747,4 м.

Лекция№4

4.1 Ориентирование линий

Задание 4.1.1

Вычислить географический (истинный) азимут линии АВ по известному магнитному азимуту и магнитному склонению (табл. 4.1.1). Нарисовать схему.

Таблица 4.1.1 − Данные для задания 4.1.1

Задание 4.1.2

Определить дирекционный угол αВА обратного направления линии АВ по известному дирекционному углу αАВ прямого направления (табл. 4.1.2). Нарисовать схему.

Таблица 4.1.2 − Данные для задания 4.1.2

Задание 4.1.3

Вычислить истинный румб линии rСD по известному истинному азимуту АCD (табл. 4.1.3). Нарисовать схему.

Таблица 4.1.3 Данные для задания 4.1.3

Задание 4.1.4

Вычислить дирекционный угол линии 3-4 по известному дирекционному углу линии 2-3 и горизонтальному углу на точке 3 (табл. 4.1.4).

Нарисовать схему.

Таблица 4.1.4 Данные для задания 4.1.4

Задание 4.1.5

Вычислить горизонтальный угол АВС по известным дирекционным углам линии ВА и линии ВС (табл. 4.1.5). Нарисовать схему.

Таблица 4.1.5 Данные для задания 4.1.5

Задание 4.1.6

Вычислить дирекционный угол линии АВ по известному магнитному азимуту АМ, магнитному склонению (δ) и сближению меридианов (γ) (табл. 4.1.6).

Нарисовать схему.

Таблица 4.1.6 Данные для задания 4.1.6