Добавил:

el_rad1o Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Преобразователи информации и датчики физических величин

Файл:

ДФВ_ЛР4 Лабораторная№6 калибровка МЭМС акселерометра

.pdf

Скачиваний:

Добавлен:

01.07.2024

Размер:

939.24 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Лабораторная работа №4 Калибровка МЭМС акселерометра

1. Теоретические сведения

Акселерометр – датчик линейного ускорения, измеряет проекцию вектора кажущегося ускорения на ось чувствительности. Вектор кажущегося ускорения равен разности вектора абсолютного ускорения объекта и вектора ускорения свободного падения .

= −

Электронные акселерометры применяются для измерения линейных ускорений движущихся объектов, измерения параметров вибрации и ударных нагрузок, а также для измерения углов наклона.

Большое распространение получили электронные акселерометры,

изготавливаемые по поверхностной интегральной технологии. Форма представления выходного сигнала акселерометра может быть аналоговой или цифровой.

Погрешность показаний акселерометра включает в себя аддитивную составляющую (постоянное смещение), мультипликативную (изменение коэффициента передачи), а также случайную составляющую.

С целью компенсации погрешностей и получения наиболее близкого к истинному значения ускорения датчики ускорения калибруют. Процесс калибровки может осуществляться статически – в этом случае анализируется воздействие на датчик ускорения свободного падения. Для динамической калибровки применяются центрифуги и вибрационные стенды, позволяющие воспроизвести требуемые параметры ускорения.

1.2 Модель погрешности одноосевого акселерометра.

Цифровой код, формируемый на выходе одноосного акселерометра,

может быть представлен выражением (1):

			=	( + )	+		(1)
				0
где		– коэффициент преобразования,			= 1[ед. к⁄	];

0	– аддитивная погрешность измерения ускорения;
		– значение проекции		действующего ускорения			на ось

чувствительности датчика, = 1[ ];

– случайная составляющая погрешности выходного сигнала.

В общем случае между осью чувствительности акселерометра и вектором действующего ускорения может быть некоторый угол.

Распространенной причиной этого является погрешность установки датчика,

крен при пайке и т.д.

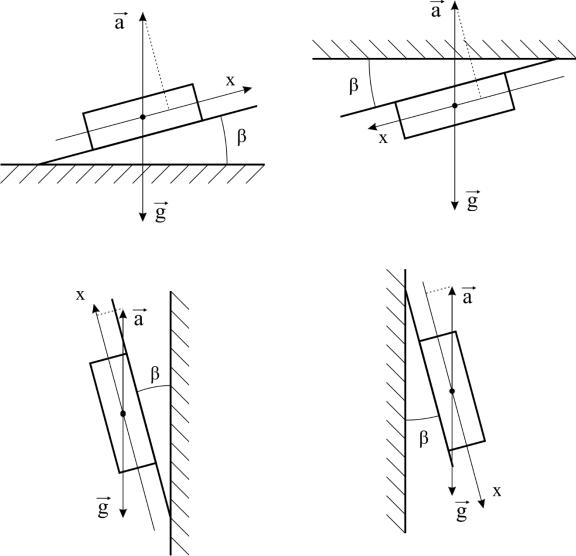
На рисунке 1 показаны примеры установки акселерометра на горизонтальном и вертикальном основании с малой погрешностью угла установки. Для приведенных на рисунках а) и в) примеров с учетом малости

значения проекции могут быть выражены следующими соотношениями (2), (3):

	= \| \| ∙ cos (			− ) = ∙ sin( ) ≈ ∙	(2)
1	= \| \| ∙ cos (			− ) = ∙ sin( ) ≈ ∙	(2)
1			2
			2
		3	= \| \| ∙ cos(β) = ∙ cos( ) ≈		(3)
		3

а)

б)

в) г)

Рисунок 1 – Ориентационные положения одноосевого акселерометра.

Из соотношений (4)-(7) можно выразить неизвестные параметры:

4 = (0 − )

3 = (0 + )

2 = (0 − )

1 = (0 + )

Выразим значения показаний акселерометра для каждого положения:

(4)

(5)

(6)

(7)

Методика калибровки одноосевого датчика

Используя приведенную модель погрешности, можно провести калибровку акселерометра. Калибровка проводится в статическом режиме, с

использованием ускорения свободного падения. В процессе калибровки ось чувствительности датчика устанавливается в 4 различных положения относительно направления действия ускорения свободного падения (см.

рисунок 1).

Случайная погрешность может быть скорректирована путем проведения серии экспериментов для каждого с последующим усреднением.

3−4

(8)

3+ 4

∙

3+ 4

∙

(9)

3−4

1.3 Модель погрешности трехосевого акселерометра.

При использовании трехосевого акселерометра показания каждого акселерометра включают:

1) значение проекции ускорения на ось чувствительности. Данное значение вносит вклад в формирование выходного значения N c

коэффициентом (1 + ). Где

− относительная погрешность коэффициента преобразования;

n – название оси чувствительности.

2) влияние проекций ускорения на другие оси координат объекта

∙ .

– коэффициент влияния поперечного ускорения;

n, m, l – названия осей чувствительности;

n – ось, для которой составляется выражение;

l – ось, относительно которой действует паразитная составляющая ускорения.

3)постоянное смещение оценки ускорения 0

4)случайная погрешность

Составляющие ускорения при формировании выходного значения умножаются на коэффициент преобразования:

= 1[ед. к.⁄ ];

Для трех осей система уравнений приобретает вид:

[(1 +

)

−

] +

(10)

[−

(1 +

)

] +

(11)

[

−

+ (1 +

)

] +

(12)

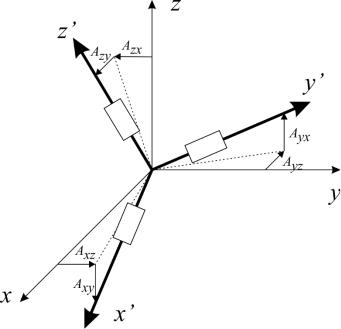
Знак коэффициентов влияния паразитных составляющих выбирается в соответствии с представлением о повороте осей чувствительности датчика относительно координатных осей объекта (Рисунок 2):

Рисунок 2 – Положение осей чувствительности датчика относительно координатных осей объекта.

Представим приведенную выше систему уравнений в матричной форме:

(1 + )

−

[

] = [

] ∙ ([

−

(1 + )

] ∙ [ ] + [ 0]) + [ ]

(13)

−

(1 +

)

Методика калибровки трехосевого акселерометра

Калибровка трехосевого датчика предполагает экспериментальное определение неизвестных параметров: , , , , 0 для всех осей чувствительности.

a) В положении О1 (см. Приложение А) проекции ускорения на оси чувствительности датчика принимают следующие значения:

= , = = 0.

С учетом этого выражение (10) принимает вид:

	=		[(1 +		) +				0	]	+	(14)
1									0		х
	=		[−	+			0	] +				(15)
1							0
	=	[		+	0	] +						(16)
1					0

В положении О2: = −,					=		= 0.

	=	[−(1		+		) + ]		+	(17)
2							0	х
	=	[	+		0	]	+		(18)
2					0
	= [−			+			] +		(19)
2					0

Случайные погрешность							исключаются путем		усреднения

результатов серии экспериментов.
	+	= 2		;
1	2		0
								+
					=		1	2	(20)
					=				(20)
				0			2
							2
	−	= 2	(1 +			) ;
1	2

										−
						=			1	2	− 1	(21)
						=					− 1	(21)
								2
								2
Зная величину выражений (15) (18) определим степень влияния

поперечной составляющей ускорения и смещения нуля по оси y.
	+	= 2		;
1	2		0
						+
			=		1	2						(22)
			=									(22)
		0			2
					2
	−	= 2		;
2	1
						−
			=		2		1					(23)
			=									(23)
					2
					2
Аналогично для оси z:
				+
			=		1	2						(24)
			=									(24)
		0			2
					2
						−
			=		1	2						(25)
			=									(25)
					2
					2

б) В положении О3 (см. Приложение А) проекции ускорения на оси чувствительности датчика принимают следующие значения:

= , = = 0.

С учетом этого выражение (10) принимает вид:

3 = [ + 0] + х

3 = [(1 + ) + 0] +

3 = [− + 0] +

Для положения О4:

	=		[−	+			] +
4					0		х
	=		[−(1	+		) +		] +
4							0
	=	[		+	] +
4				0

Аналогично расчетам, произведенным в перечислении а):

				+
	=		3			4
	=
0			2
			2
					−
	=		3			4	− 1
	=						− 1
			2
			2
				+
	=		3		4
	=
0			2
			2
				−
	=		3			4
	=
			2
			2
		+
	=		3		4
	=
0			2
			2
				−
	=		4		3
	=
			2
			2

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

б) В положении О5 (см. Приложение А) проекции ускорения на оси чувствительности датчика принимают следующие значения:

= , = = 0.

С учетом этого выражение (10) принимает вид:

5 = [− + 0] + х

5 = [ + 0] +

5 = [(1 + ) + 0] +

Для положения О6:

6 = [ + 0] + х

6 = [− + 0] +

6 = [−(1 + ) + 0] +

Аналогично расчетам, произведенным в перечислении а):

				+
	=	5				6
	=
0			2
			2
				−
	=	5				6	− 1
	=						− 1
		2
		2
					+
	=	5				6
	=
0			2
			2
						−
	=		6			5
	=
		2
		2
					+
	=	5				6
	=
0			2
			2
						−
	=		5			6
	=
		2
		2

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лабораторная работа №6

#
01.07.2024939.24 Кб0ДФВ_ЛР4 Лабораторная№6 калибровка МЭМС акселерометра.pdf
#
01.07.2024501.21 Кб0ПреобразователиМЭМС_Готово.docx