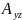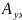МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет «МИЭТ»

Институт «Микроприборов и систем управления» (МПСУ)

Лабораторная работа №4 по теме:

«Калибровка МЭМС акселерометра»

Выполнили студенты группы «KEK-$$»:

EL_BIBA

EL_BOBA

EL_RADIO

EL_ZELIBOBA

Преподаватель:

Страчилов Максим Васильевич(KAEFF PREPOD)

Зеленоград 2024 г.

Теоретические сведения

Акселерометр – датчик линейного ускорения, измеряет проекцию вектора кажущегося ускорения на ось чувствительности. Вектор кажущегося ускорения 𝑎⃗ равен разности вектора абсолютного ускорения 𝑤⃗ объекта и вектора ускорения свободного падения 𝑔⃗.

𝑎⃗ = 𝑤⃗ − 𝑔⃗

Электронные акселерометры применяются для измерения линейных ускорений движущихся объектов, измерения параметров вибрации и ударных нагрузок, а также для измерения углов наклона.

Большое распространение получили электронные акселерометры, изготавливаемые по поверхностной интегральной технологии. Форма представления выходного сигнала акселерометра может быть аналоговой или цифровой.

Погрешность показаний акселерометра включает в себя аддитивную составляющую (постоянное смещение), мультипликативную (изменение коэффициента передачи), а также случайную составляющую.

С целью компенсации погрешностей и получения наиболее близкого к истинному значения ускорения датчики ускорения калибруют. Процесс калибровки может осуществляться статически – в этом случае анализируется воздействие на датчик ускорения свободного падения. Для динамической калибровки применяются центрифуги и вибрационные стенды, позволяющие воспроизвести требуемые параметры ускорения.

Модель погрешности одноосевого акселерометра.

Цифровойкод,формируемыйнавыходеодноосногоакселерометра,можетбытьпредставленвыражением (1):

𝑁_𝑋=𝐾_𝐴𝑋⁽𝑎₀+𝑎_𝑥⁾+𝑁_𝜁 (1)

^{Где –коэффициентпреобразования,𝐾𝐴𝑋=1}[^ед.к⁄_𝑔]^;

𝑎₀– аддитивная погрешность измерения ускорения;

𝑎_𝑥 – значениепроекциидействующегоускорениянаосьчувствительностидатчика, 𝑎_𝑥=1^[𝑔^];

𝑁_𝜁–случайная составляющая погрешности выходного сигнала.

В общем случае между осью чувствительности акселерометра и вектором действующего ускорения может быть некоторый угол. Распространенной причиной этого является погрешность установки датчика, крен при пайке и т. д.

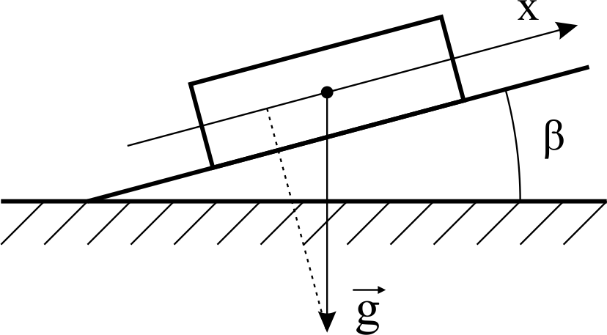
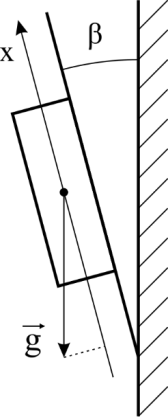
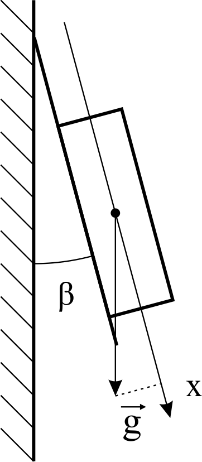
Рисунок1–Ориентационные положения одноосного акселерометра.

На рисунке 1 показаны примеры установки акселерометра на горизонтальном и вертикальном основании с малой погрешностью 𝛽 угла установки. Для приведенных на рисунках а) и в) примеров с учетом малости 𝛽 значения проекции 𝑎𝑥 могут быть выражены следующими соотношениями (2), (3):

𝑎𝑥1 = |𝑎⃗| ∙ cos ( 𝜋 2 − 𝛽) = 𝑔 ∙ sin (𝛽) ≈ 𝑔 ∙ 𝛽 (2)

𝑎𝑥3 = |𝑎⃗| ∙ cos(β) = 𝑔 ∙ cos(𝛽) ≈ 𝑔 (3)

Методика калибровки одноосного датчика

Используя приведенную модель погрешности, можно провести калибровку акселерометра. Калибровка проводится в статическом режиме, с использованием ускорения свободного падения. В процессе калибровки осьчувствительностидатчикаустанавливаетсяв4различныхположенияотносительнонаправлениядействияускорениясвободногопадения(см.рисунок1).

Случайнаяпогрешность𝑁_𝜁можетбытьскорректированапутемпроведениясерииэкспериментовдлякаждогоспоследующимусреднением.

Выразим значения показаний акселерометра для каждого положения:

𝑁₁=𝐾_𝑎𝑥⁽𝑎₀−𝑔𝛽⁾ (4)

𝑁₂=𝐾_𝑎𝑥⁽𝑎₀+𝑔𝛽⁾ (5)

𝑁₃=𝐾_𝑎𝑥⁽𝑎₀−𝑔⁾ (6)

𝑁₄=𝐾_𝑎𝑥⁽𝑎₀+𝑔⁾ (7)

Из соотношений (4)-(7) можно выразить неизвестные параметры:

Модель погрешности трехосевого акселерометра.

При использовании и трехосевого акселерометра показания каждого акселерометра включают:

1. Значение проекции ускорения на ось чувствительности. Данное значение вносит вклад в формирование выходного значения Nc с коэффициентом. (1+𝐴_𝑛𝑛). Где

𝐴_𝑛𝑛−относительная погрешность коэффициента преобразования;

n –название оси чувствительности.

2. Влияние проекций ускорения на другие оси координат объекта

𝐴_𝑛𝑚∙𝑎_𝑙.

𝐴_𝑛𝑚–коэффициент влияния поперечного ускорения;

n, m, l–названия осей чувствительности;

n–ось, для которой составляется выражение;

l–ось,относительнокоторойдействуетпаразитнаясоставляющаяускорения.

3. Постоянноесмещениеоценкиускорения𝑎_0𝑛

4. Случайная погрешность

Составляющие ускорения при формировании выходного значения умножаются на коэффициент преобразования:

^{𝐾𝑎𝑛=1}[^ед.к.⁄_𝑔]^;

Для трех осей система уравнений приобретает вид:

𝑁_𝑋=𝐾_𝐴𝑋[⁽1+𝐴_𝑥𝑥⁾𝑎_𝑥+𝐴_𝑥𝑧𝑎_𝑦−𝐴_𝑥𝑦𝑎_𝑧+𝑎_0𝑥]+𝑁_𝜁х (10)

𝑁_𝑌=𝐾_𝐴𝑌[−𝐴_𝑦𝑧𝑎_𝑥+(1+ 𝐴_𝑦𝑦)𝑎_𝑦+ 𝐴_𝑦𝑥𝑎_𝑧+𝑎_0𝑦] +𝑁_𝜁𝑦 (11)

𝑁_𝑍=𝐾_𝐴𝑍[𝐴_𝑧𝑦𝑎_𝑥−𝐴_𝑧𝑥𝑎_𝑦+(1+𝐴_𝑧𝑧)𝑎_𝑧+𝑎_0𝑧]+𝑁_𝜁𝑧 (12)

Знак коэффициентов влияния паразитных составляющих выбирается в соответствии с представлением о повороте осей чувствительности датчика относительно координатных осей объекта (Рисунок2):

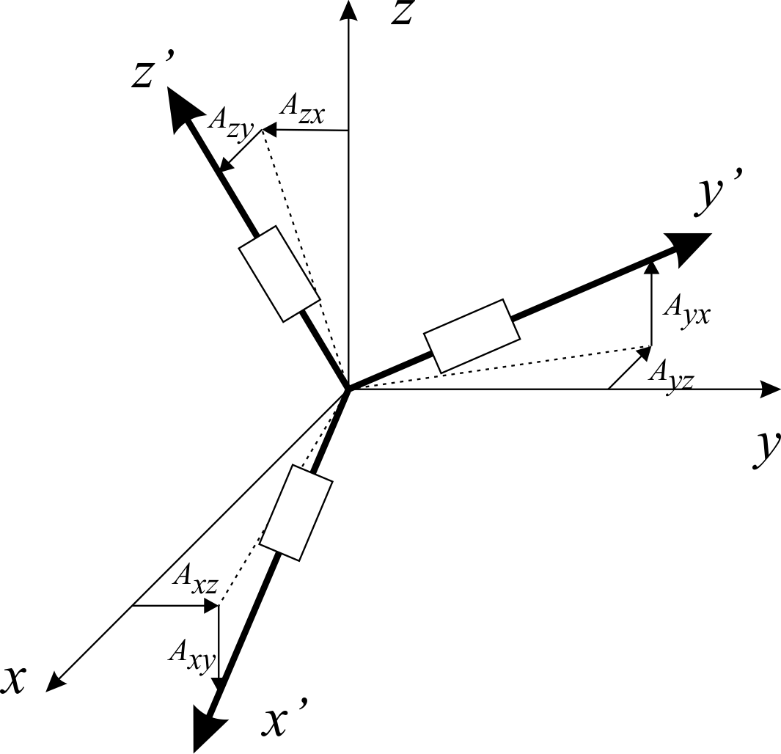
Рисунок2–Положениеосейчувствительностидатчикаотносительнокоординатныхосей объекта.

Представим приведенную выше систему уравнений в матричной форме:

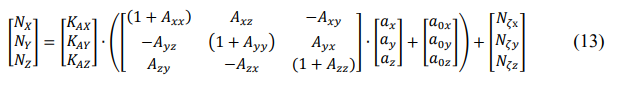
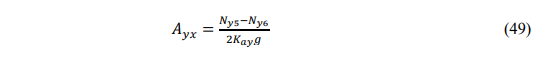
Выполнение работы

1. Сборка рабочего места

1. Установили модуль МК на контактной макетной плате.

2. Подключили разъёмы модуля датчика к макетной плате согласно рисунку 3:

Рисунок 3. - модуль микроконтроллера на контактной макетной плате

3. Подключили модуль к ПК с помощью USB.

4. Через приложение mems1.exe осуществили чтение из регистров.

2. Калибровка одноосного акселерометра

Занесли в таблицу 1 содержимое регистров одноосного акселерометра и преобразовали результат из шестнадцатеричной в десятеричную систему счисления.

	N1		N2		N3		N4
	h	l	H	l	h	l	h	l
Измерение 1	0xfb	0x7f	0xff	0xe8	0x3e	0x40	0xbf	0xac
Измерение 2	0xfc	0xdc	0xfe	0x58	0x3f	0x3c	0xbf	0x38
Измерение 3	0xfd	0xe8	0xff	0xa4	0x3f	0xb8	0xbf	0x44
Измерение 4	0xfd	0xcc	0xff	0xc4	0x3f	0x38	0xbe	0xec
Результат	-764		-150		16155		-16474.5

Таблица 1 – Данные исследования одноосевого датчика.

3. Калибровка трехосного акселерометра

Аналогично пункту 2, сняли совокупность значений в 6 ориентациях по трем осям и усреднили результаты по каждому значению, записав в таблицу 2.

	O1	O2	O3	O4	O5	O6
Nx	16127	-16571	413	-761	-403	-150
Ny	-587	360,25	16717	-16508	-313	-151
Nz	-234	-476	-423	-433	16212	-17033

Таблица 2 – Данные исследования трехосного датчика.

4. Обработка экспериментальных данных

Рассчитали значения калибровочных коэффициентов с помощью формул, приведенных в теоретической части и записали в таблицу 3 – для одноосевого датчик, в таблицу 4 – для трехосного:

1664,77	-0,096	-0,0188

Таблица 3 – Калибровочные коэффициенты одноосевого датчика.

, g	-0,133072	-0,1043	-0,166
, g	-0,06688	0,06165	-0,13686
, g	-0,209295	0,505262	-0,242016
	-2,81*	-	-
	-	1,81*	-
	-	-	2,045*
	0,2794	-	-
	-0,2792	-	-
	-	0,036	-
	-	-0,0003	-
	-	-	0,009572
	-	-	-0,004876

Таблица 4 – Калибровочные коэффициенты трехосного датчика.

5. Вывод NET BLIN VVOD

В ходе данной лабораторной работы мы изучили принципы работы микроэлектромеханического (МЭМС) акселерометра в одноосном и трехосном режимах измерения. Процесс калибровки позволяет скомпенсировать систематические ошибки и повысить точность измерений.

Для одноосного режима мы экспериментально определили калибровочные коэффициенты смещения и масштабирования. В трехосном режиме мы вычислили матрицу калибровочных коэффициентов, учитывая перекрестные влияния между осями. Полученные калибровочные данные могут быть использованы для компенсации погрешностей акселерометра в реальных приложениях, обеспечивая более точные измерения ускорения в одной или нескольких осях.