1 6. Основные характеристики влажного воздуха, методы их определения.

ОСНОВНЫЕ СВОЙСТВА ВЛАЖНОГО ВОЗДУХА можно с достаточной точностью определить с помощью диаграммы , разработанной Л.К.Рамзиным (рис. 25.1.). Угол между осями координат данной диаграммы равен 135°, при этом на оси ординат отложены значения энтальпии, а на оси абсцисс – значение влагосодержания. Для удобства пользования диаграммой ось абсцисс спроектирована на горизонтальную ось.

На диаграмме нанесены следующие линии:

постоянного влагосодержания ( ) – вертикальные прямые, параллельные оси ординат;

постоянной энтальпии ( ) – прямые, параллельные оси абсцисс, т.е. идущие под углом 135° к горизонту;

постоянных температур ( ) – прямые, идущие с некоторым наклоном;

постоянной относительной влажности ( ) - расходящийся пучок кривых;

парциальных давлений водяного пара во влажном воздухе, значения которых отложены в нижней части правой оси ординат.

С помощью диаграммы можно по двум известным параметрам найти все остальные, характеризующие состояние данного воздуха, или изобразить изменение этих параметров в процессе нагрева воздуха и сушки материала.

Влагосодержание воздуха можно рассчитать по уравнению , где – общее давление паровоздушной смеси, Па; – давление насыщенного водяного пара при температуре воздуха.

Энтальпию (теплосодержание) влажного воздуха относят к 1 кг абсолютно сухого воздуха и определяют как сумму энтальпий 1 кг абсолютно сухого воздуха и кг пара:

, где и – средние удельные теплоёмкости абсолютно сухого воздуха и водяного пара соответственно, кДж/(кг*К); – удельная теплота фазового превращения при 0 °С, кДж/кг.

Температура точки росы – это температура, до которой необходимо охладить влажный воздух, чтобы он перешёл в состояние насыщения при постоянном влагосодержании ( ).

Температура мокрого термометра – температура, до которой необходимо охладить влажный воздух, чтобы он перешёл в состояние насыщения при адиабатических условиях, т.е. при постоянной энтальпии ( ).

Относительной влажностью воздуха называется отношение фактической массы водяных паров в воздухе к максимально возможной при тех же температуре и давлении. Т.к. содержание паров в воздухе можно характеризовать парциальным давлением, то относительная влажность равна .

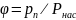17. I – x диаграмма Л.К.Рамзина и её практическое использование. (см. вопрос 16)

Основные свойства влажного воздуха можно с достаточной точностью определить с помощью диаграммы I – x, разработанной Л.К. Рамзиным (рис. 25.1). Угол между осями координат данной диаграммы равен 135°, при этом на оси ординат отложены значения энтальпии, а на оси абсцисс – значения влагосодержания. Для удобства пользования диаграммой ось абсцисс спроектирована на горизонтальную ось.

На диаграмме нанесены следующие линии: [см. вопрос 16]

18. Уравнение теплового баланса реальной сушилки.

Уравнение теплового баланса воздушной конвективной сушилки имеет вид , где – количество теплоты, затраченное на нагрев воздуха в калорифере, Вт; , , – энтальпия воздуха перед калорифером, на входе и выходе из сушилки, Дж/кг; – массовый расход высушенного материала, рассматривается как разность расходов влажного материала и испаренной влаги , кг/с; , – удельные теплоёмкости высушенного материала и влаги, Дж/кг*К; , - температуры материала на входе и выходе из сушилки, °C; – масса транспортных устройств, кг; – удельная теплоёмкость материала, из которого изготовлены транспортные устройства, Дж/кг*К; , - потери теплоты в окружающую среду, Вт.

Решением данного уравнения относительно количества теплоты Q является выражение , Вт; Здесь – количество теплоты в уходящем из сушилки воздухе, Вт; - количество теплоты, расходуемой на нагрев материала, Вт; - количество теплоты, расходуемой на нагрев транспортных устройств, Вт; - количество теплоты, приходящей с испаряемой из материала влагой, Вт.

Разделив все члены уравнения (25.6) на W и обозначив удельные расходы теплоты и воздуха соответствующими строчными буквами, получим .

Обозначим последние четыре члена правой части данного уравнения через и, представляя удельный расход теплоты в калорифере как , запишем или

––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

, где

, – энтальпия воздуха на входе и выходе из сушилки, Дж/кг;

– удельный расход воздуха, кг воздуха/кг влаги, (величина, характеризующая расход сушильного агента на 1 кг испаренной влаги);

Это равенство является уравнением теплового баланса реальной сушилки. Входящая в уравнение величина может иметь положительное или отрицательное значение или может быть равной нулю. В последнем случае энтальпии , и такая сушилка называется теоретической. Процесс сушки в ней протекает адиабатически при постоянной энтальпии воздуха , при этом испаряемая из материала влага вносит в воздух столько теплоты, сколько он отдаёт, охлаждаясь, на испарение влаги. Удельный расход теплоты в теоретической сушилке находится по уравнению .