1846

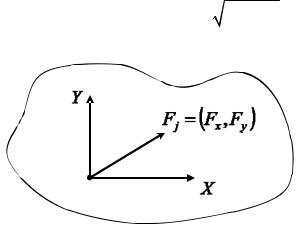
Уравнения (25) и (26) можно представить в форме

Здесь i принимает решения от единицы до N , а граничные коэффициенты влияния Bssij us Fsi ds, ... можно вычислить по контрольным

s j

решениям.

Система линейных уравнений (27) позволяет вычислить неизвестные граничные параметры (перемещения и напряжения) прямо по заданным граничным условиям.

Построение контрольных решений выполняется, вообще говоря, для сосредоточенной силы, приложенной в точке бесконечной упругой среды. Задача о действии сосредоточенной силы в точке бесконечной упругой среды известна как задача Кельвина [34]. Задача Кельвина для условий плоской деформации иллюстрируется рис. 120. Решение этой задачи выражается через функцию g x, y , определяемую формулой

Рис. 120

Перемещения при этом будут равны:

251

Заметим, что сосредоточенная сила Fi Fx , Fy была помещена в начале координат. Если эту силу расположить в точке x cx , y cy , то в решении (28)-(31) нужно заменить координаты x и y на преобразованные

координаты x cx и y cy .

В прямом методе граничных интегралов граничные коэффициенты влияния получают путём приложения сосредоточенной силы (с ком-

понентами Fsi и Fni ) в средней точке i-го отрезка контура C и интегри-

рования перемещений и напряжений, вызванных этими силами, вдоль j-го отрезка в соответствии с формулами (25) и (26). Изменяя i от единицы до N , то есть прикладывая поочерёдно N сосредоточенных сил по контуру, получаем необходимую систему алгебраических уравнений (27).

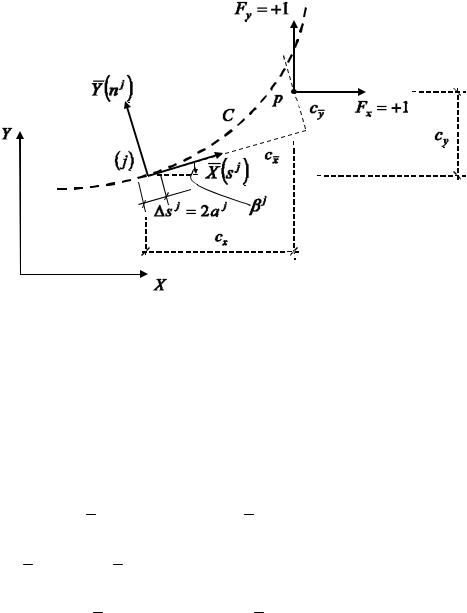
При вычислении коэффициентов влияния Bssij , ... воспользуемся локальной системой координат x, y с началом в центре j-го отрезка контура C (рис. 121). Эти координаты соответствуют обычным локальным координатам s j и n j , причём ось x (или s j ) направлена по направлению обхода контура, а ось y (или n j ) направлена вне рассматриваемой области.

Принятые направления обхода контура показаны на рис. 121. Мы хотим вычислить перемещения и напряжения на j-м отрезке, вызванные действием сосредоточенной силы, приложенной в центре i-го отрезка. Компоненты

этой силы, параллельная и перпендикулярная i-му отрезку, равны Fsi и Fni

252

соответственно. Из рис. 121 легко видеть, что компоненты этой силы в

Здесь i j .

формулах (29)–(30) на x cx и y c y и изменением координатных индексов

~s xy , ~n y на j-м отрезке (наше контрольное решение) находим из полученных выражений, подставляя в них y 0 и учитывая соотношения (32):

253

s Fsi 1 2 gx sin 1 2 gy cosx2 gy x cx cos x2 gy cy sin

Fni 1 2 gx cos 1 2 gy sin

x2 gy x cx sin x2 gy cy cos ;

Fni 2 gx sin 2 1 gy cos

2 g x cx sin 2 g cy cos .

y2 y2

g x, y и её производные определяются в выражениях (33) и (34) при y 0.

Выражения (33) и (34) дают два контрольных решения для каждого конечного элемента i : одно – для касательной силы Fsi , другое для

зависимости (25) и (26) и выполнения необходимого интегрирования вдольs j , то есть интегрирования по x в пределах от a j до a j . Поскольку в

полученных при этом уравнениях силы Fsi и Fni входят и в левую, и в правую части уравнений, то их можно считать равными +1.

254

Итак, получаем:

a j

1 2 T2 sin 2 1 T3 cos cy T4 sin T5 cos .

Здесь T1, ..., T5 это определённые интегралы от функции g x, y и её производных (вычисленных при y 0):

255