19. Коррекция сау. Способы коррекции линейных сау.

Для того чтобы добиться желаемого качества процесса управления (требуемой точности и качества переходного процесса) есть 2 пути:

1. Достигнуть этого путём изменения параметров данной системы.

Если же путём изменения параметров данной системы не удаётся получить желаемого результата используют 2 путь:

2. изменение структуры системы. Осуществляется путём введения дополнительных устройств или звеньев. Эти дополнительные звенья называют корректирующими звеньями или корректирующими устройствами.

Основная задача корректирующих устройств состоит в улучшении точности и качества переходных процессов.

Наряду с этим корректирующие устройства позволяют решать и более общую задачу. Позволяют сделать систему устойчивой если она была неустойчива и затем уже добиться желаемого качества управления.

Различают 3 основных вида корректирующих устройств:

1. Последовательные корректирующие устройства.

Повышается точность системы, повышается быстродействие.

Для рисунка а) W(S) = W_k(S)W₀(S)

W₀(S) – передаточная функция исходной или корректирующей системы.

Для рисунка б) W_к(S) = W_ос(S) + W_к1(S)

2. Параллельное корректирующее устройство

W_ос(S) (дополнительные местные обратные связи) охватывает звено или часть системы.

3. Корректирующие устройства по внешнему воздействию.

Передаточные функции W_к(S), W_ос(S) могут иметь произвольный вид, но чаще применяются корректирующие устройства определённого вида.

Действия корректирующих звеньев сводиться к следующему:

1. Введение в контур САУ воздействия по производным и интегралам.

2. Введение корректирующих обратных связей вокруг определённой части системы.

3. Введение корректирующих воздействий функций внешних воздействий и их производных.

Введение воздействий по производным и интегралам осуществляется с помощью последовательных корректирующих устройств. Организация местных обратных связей осуществляется с помощью параллельных корректирующих устройств.

20. Разновидности корректирующих обратных связей в линейных САУ.

а

21. Точность линейных САУ при случайных стационарных входных воздействиях.

а

22. Понятие и условия инвариантности линейных САУ. Комбинированное управление по задающему воздействию.

а

23. Понятие и условия инвариантности линейных САУ. Комбинированное управление по возмущающему воздействию.

а

24. Основные свойства линейных САУ. Чувствительность.

Параметры САУ (коэффициент усиления, постоянная времени) зависит от физических параметров элементов, входящих в систему (сопротивление, ёмкость и индуктивность).

В процессе эксплуатации системы эти физические параметры могут изменятся во времени. Поэтому возникает задача определения влияния изменения параметров системы на статические и динамические свойства процесса управления.

Степень влияния изменения параметров системы на её статические и динамические свойства называют чувствительностью системы.

Существуют методы анализа чувствительности и методы достижения малой чувствительности в проектируемых системах.

П усть сиcтема описывается уравнением в нормальной форме:

Изменяющиеся со временем параметры системы обозначим через j j = 1,m.

Эти изменяющиеся параметры входят в коэффициенты уравнения:

Процессы в системе (2) при неизменённых параметрах определяются решениями вида:

x₁(t), x₂(t) … x_n(t) – это исходные решения.

Процессы в той же системе, но с изменяемыми параметрами, которые определяются решениями уравнения (3) называют варьируемым движением.

x₁(t), x₂(t) … x_n(t)

Возникающие различия можно обозначить за x_i(t) = x_i(t) – x_i(t)

x_i(t) – дополнительное движение системы.

При малых изменениях параметра j можно записать:

Если в этом уравнении ввести обозначения

(4) то дополнительное движение системы

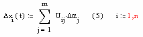
Величины Uij называют функциями чувствительности.

Аналогичные характеристики чувствительности вводятся так же и для различных показаний качества системы. в этом случае в формуле (4) вместо координаты состояния будет стоять соответствующий показатель качества системы. А в формуле (5) вместо изменения координат системы будет стоять изменение этого показателя качества.

Функцией чувствительности для частотных характеристик будут функции не времени а частот. Когда показатель качества выражается не функцией а числом, тогда Uj станет не функцией, а коэффициентом чувствительности.

Определение функции чувствительности производится следующим образом:

Если продифференцировать (*) по j, то получим:

Если в левой части поменять порядок дифференцирования, то получим:

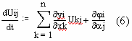
Выражение (6) – уравнение чувствительности.

Непосредственное определение функции чувствительности Uij по этим уравнениям затруднительно, поэтому используют модели или графы

Пример:

Определить чувствительность для системы:

(Tp + 1)y(t) = kx(t), чувствительность по Т и по к - ?

Введём 2 функции чувствительности.

Перепишем уравнение в стандартной форме:

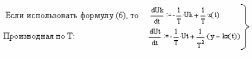- уравнения чувствительности для данной системы

Что же касается функции и коэффициентов чувствительности для показателей качества, то их определяем проще, поскольку там не будет дифференцирования.