6. Соединения звеньев сау. Математическое описание соединений линейных звеньев сау.

При исследовании САУ можно разбить систему на комбинацию динамических звеньев с известными передаточными функциями. Будем считать динамические звенья направленными и независимыми, т.е. такими, сигналы которых проходят от входа к выходу, а подключение последующих звеньев не влияет на характер переходных и установившихся процессов предыдущих звеньев. В САУ существует три способа соединения звеньев: последовательное, параллельное и с обратной связью (ОС).

Рис. 2.19

Последовательное соединение изображено на рис. 2.19. При последовательном соединении звеньев выходной сигнал предыдущего звена является входным сигналом для последующего звена, а результирующая передаточная функция равна произведению передаточных функций отдельных звеньев.

^{W(р)=W1(р)W2(р)*...*Wn(P)=} . (2.27)

При параллельном соединении (рис. 2.20) на вход всех звеньев подается общий сигнал, а на выходе образуется сигнал, являющийся суммой выходных сигналов звеньев.

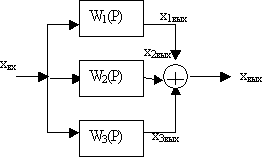
Рис. 2.20

Результирующая передаточная функция является суммой передаточных функций звеньев.

^{W(р)=W1(р)+W2(р)+...+Wn(P)=} (2.28)

При соединении с ОС выходной сигнал первого звена является входным для второго, причем входной сигнал первого

звена образуется в результате сложения или вычитания входного сигнала и выходного сигнала второго звена.

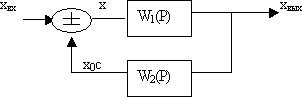
Рис. 2.21

Передаточная функция системы при соединении с обратной связью рассчитывается по формуле

W₁(р)

W(р)= (2.29)

1  W₁(р) W ₂ (р)

где знак минус в (2.29) ставится при положительной обратной связи, а плюс - при отрицательной обратной связи.

Если второе звено в цепи обратной связи отсутствует, то

W₁(р)

W(р)= . (2.30)

1  W₁(р)

Таким образом, имея структурную схему САУ и зная передаточные функции звеньев, можно найти передаточную функцию САУ и проводить с её помощью исследование САУ на точность, быстродействие и устойчивость.

7. Многомерные сау. Модели вход-выход многомерных линейных сау.

Особенности многомерных САУ. Многомерными или много связанными системами называют такие системы которые имеют 2 или несколько входных задающих воздействий. При этом может быть любое количество возмущающих воздействий.

Математическая модель «вход-выход» – это описание связи входных и выходных сигналов динамической системы. Необходимость в таком описании появляется при рассмотрении поведения как отдельных блоков и, в частности, объекта управления, так и всей системы управления в целом.

Многомерные системы могут включать один управляющий объект с несколькими регулирующими органами.

Взаимосвязи, образующие многомерные системы могут быть различными по своей природе, их делят на 2 категории:

1. Внутренние (естественные) связи,

2. Внешние (искусственные) связи  по отношению к объекту.

Внутренние – связи, которые физически существуют в самом объекте между выходными величинами. Математически эти связи заложены в уравнение динамики объекта.

Внешние – связи организуемые в системе управления (напрямую между регуляторами), на входе, на выходе и междукаскадные.(Добиться сепаратного либо связанного управления). Задача внеш-х связей м.б. двоякой:

1. Требуется организовать определённые взаимосвязи между регулируемыми величинами.

2. Требуется при помощи внешних связей м/ду регул-ми величинами вне сущ-их объектов.

Если путем введения внеш. связей удается разорвать физ-ки сущ=ие связи, то в этом случае мы переходим к автономному регулированию каждого из параметров.

Если система многомерна то –

Можно записать передаточную функцию разомкнутой системы в отдельности для каждой регулируемой величины y_i по каждому входному воздействию x_k.

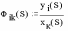
Для возмущающего воздействия –

Совокупность этих передаточных функций можно выписать в одной передаточной матрице.

Для передаточной матрицы по возмущению Ф_в(S) будет записано в m – столбцов; таким образом динамика многомерной системы в отношение от одномерной определяется либо сложной системой уравнений вида (1) либо передаточной матрицей вида (3).

Может быть составлена матрица весовых функций k(t) и матрица переходных функций Н(t).

На базе этих уравнений и передаточных матриц можно исследовать точность системы, качество переходных процессов, устойчивость системы, а так же проводить синтез корректирующих устройств.  разработаны различные приёмы с применением структурных преобразований. Эти приёмы позволяют прийти к упрощённым эквивалентным схемам.

В некоторых случаях удаётся разбить общую систему на ряд более простых систем.

Этот процесс называется декомпозиция. И оп поведению отдельных сепаратных систем можно судить о поведении систем в целом.

Перекрёстные связи могут содержаться либо в самом объекте, либо в схемах регулятора.