
ИО3
.docxЦель работы: найти решение задачи эвакуации и задачи о загрузке ресурсов.
Вариант 6.

Рисунок 1- Задача эвакуации
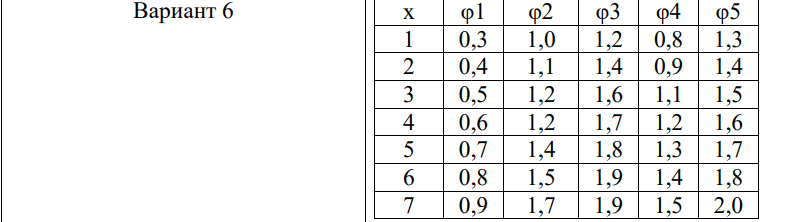
Рисунок 2- Задача о распределении ресурсов
Ход работы:
Решение задачи о загрузке (задача эвакуации)
Рисунок 3- Задача
Ограничение:

Целевая
функция:

-
S
П5
П4
П3
П2
П1










0
1
2
3
4
5
6
7
8
9
10
11
0
0
0
0
0
1
1
1
1
1
1
1
0
0
0
0
0
60
60
60
60
60
60
60
0
0
0
0
1
0
0
0
0
1
1
1
0
0
0
0
50
60
60
60
60
110
110
110
0
0
0
0
0
0
0
0
0 или 1
0
0
0
0
0
0
0
50
60
60
60
40
110
110
110
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
30
50
60
60
60
90
110
110
110
1
130


Решение задачи распределения ресурсов
Задача заключается в оптимальном распределении ограниченного количества ресурсов между несколькими предприятиями для максимизации прибыли.
Рисунок 4- Задача
Решение данной задачи можно найти в MS Excel (Рисунок 5).
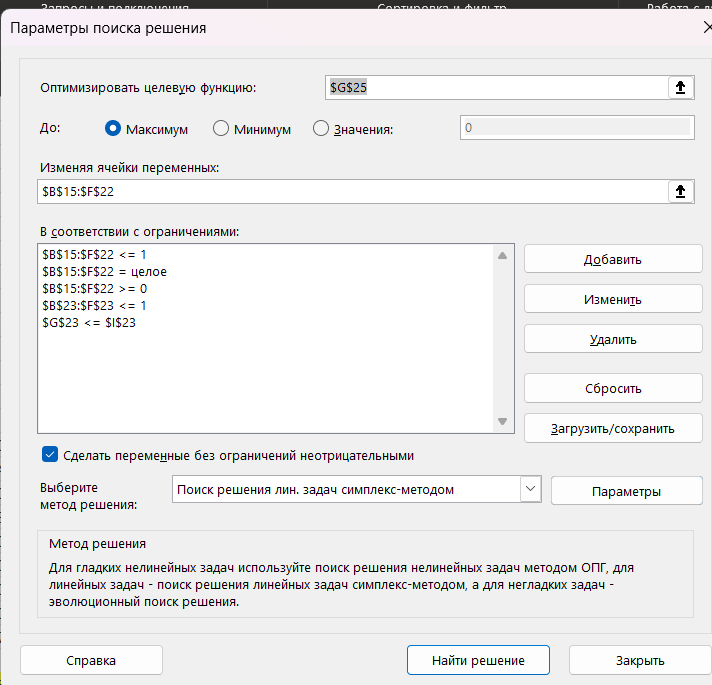
Рисунок 5- Параметры поиска решения
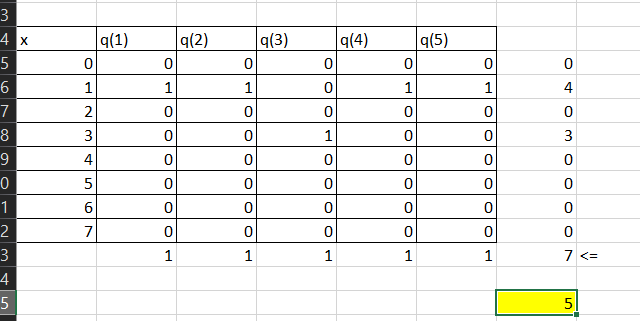
Рисунок 6-Решение задачи
Суммарный
доход составит:

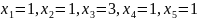
Также задачу распределения ресурсов можно решить с помощью языка программирования Python
Листинг 1- Решение задачи о распределении ресурсов
def max_price(total_resources):
# Функции прибыли для пяти предприятий
q1 = [0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
q2 = [1.0, 1.1, 1.2, 1.2, 1.4, 1.5, 1.7]
q3 = [1.2, 1.4, 1.6, 1.7, 1.8, 1.9, 1.9]
q4 = [0.8, 0.9, 1.1, 1.2, 1.3, 1.4, 1.5]
q5 = [1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 2.0]
# Таблица для хранения максимальных прибылей
table_price = [[0] * 6 for _ in range(total_resources + 1)]
# Таблица для отслеживания распределения ресурсов
table_resources = [[[] for _ in range(6)] for _ in range(total_resources + 1)]
# Заполнение таблиц
for j in range(1, 6): # Для каждого предприятия
p = q1 if j == 1 else q2 if j == 2 else q3 if j==3 else q4 if j==4 else q5
for i in range(1, total_resources + 1): # Для каждого количества ресурсов
max_price = 0
best_res = []
for x in range(min(i, len(p))): # Перебор возможного количества ресурсов
current_price = p[x] + (table_price[i - (x + 1)][j - 1] if i >= x + 1 else 0) # Вычисление текущей прибыли для данного количества ресурсов и предприятия
if current_price > max_price:
max_price = current_price
best_res = table_resources[i - (x + 1)][j - 1] + [(j, x + 1)]
table_price[i][j] = max_price
table_resources[i][j] = best_res
# Результат и путь решения
return table_price[total_resources][5], table_resources[total_resources][5]
total_resources = 7 # Общее количество доступных ресурсов
price, resource_allocation = max_price(total_resources)
print("Максимальная прибыль:", price)
print("Распределение ресурсов:")
for res in resource_allocation:
print(f"Предприятие {res[0]} получает {res[1]} ресурс(ов)")

Рисунок 7- Результат работы программы
Вывод: решена задача эвакуации ручным способом и при использовании динамического программирование найдено оптимальное решение задачи о распределении ресурсов.
Список использованных источников:
Григорьева Н.Н., Яковлева Е.А. - Учебно-методическое пособие «Базовые математические методы и модели оптимизации »‒ ГУАП, 2023
Б. К. Акопян, Е. П. Виноградова, С. М. Герасимов, Н. Н. Григорьева - Учебно-методическое пособие «Прикладные методы оптимизации»‒ ГУАП, 2019
