ИО1

Цель работы: решить задачу линейного программирования графическим методом и аналитически -симплекс-методом. Проверить решение c помощью Excel.

Вариант 1.

Ограничения:

Целевая функция:

Ход работы:

Для решения задачи графическим методом использован Desmos. На рисунке 1 показан процесс построения области допустимых значений

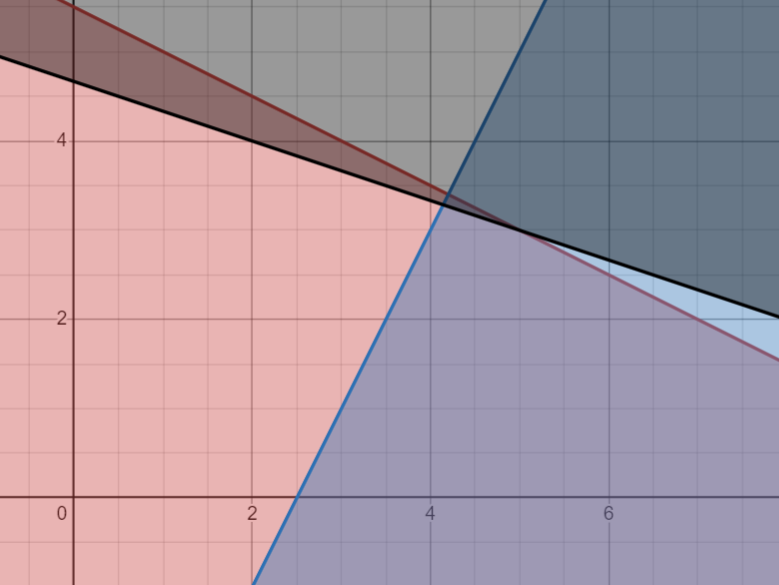
Рисунок 1- Построение области допустимых значений

Добавлен вектор V=(1,3). Перпендикулярно вектору добавлена линия x+3y=C. (Рисунок 2). Так как задача на максимум то линия двигается до самой удаленной точки ОДЗ (Рисунок 3).

Рисунок 2-Добавление вектора с линией

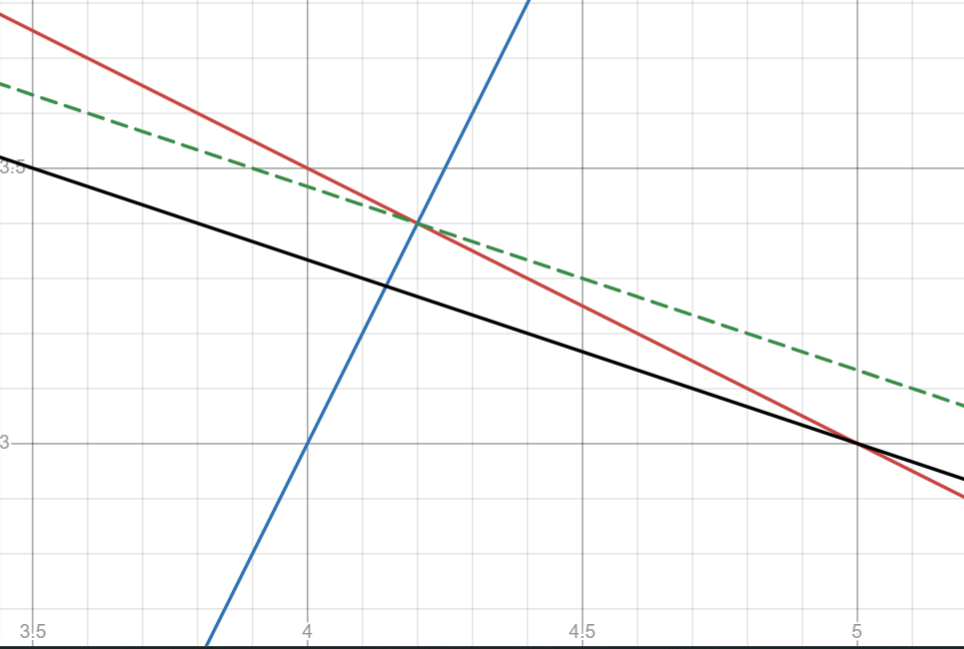
Рисунок 3- Нахождение максимума

Линия проходит через точку на голубой и красной линии, уравнения. Образуется система уравнений получим =4,2 и =3,4. Тогда F=4,2+3*3,4=14,4

Симплекс-Метод:

Для приведения задачи к канонической форме второе и третье неравенство умножены на ( -1).

Введен искусственный базис. Введены дополнительные переменные , , для каждого уравнения:

, , - базисные

, - свободные

базис	Б		(р.ст)				bi/разрещ.ст.
	11	1	2	1	0	0	11/2=5,5
(р.с)	-5	-2	1 (р.э)	0	1	0	-5/1=-5
	-14	-1	-3	0	0	1	­­-
F	0	-1	-3	0	0	0

Так как в последней строке есть отрицательные элементы, значит план неоптимальный.

Разрешающий столбец тот, у которого наименьшее число в последней строке. Вторая строка- разрешающая, так как bi/ разрешающий столбец будет наименьшим. Элемент, стоящий на пересечении разрешающего столбца и строки будет разрешающим. Значит входит в базис, выходит. Получается следующая таблица:

базис	Б	(р.ст)					bi/разрещ.ст.
	21	5	0	1	-2	0	21/5=4,2
	-5	-2	1	0	1	0	-
	-29	-7	0	0	3	1	-
F	-15	-7	0	0	3	0

Так как в строке индексов имеется отрицательная оценка, план не оптимальный. Аналогичным образом составлена следующая таблица:

базис	Б	(р.ст)					bi/разрещ.ст.
	4,2	1	0	0,2	-0,4	0
	3,4	0	1	0,4	0,2	0
	0,4	0	0	1,4	0,2	1
F	14,4	0	0	1,4	0,2	0

В последней строке все оценки положительные, либо равны 0, значит получено оптимальное решение.

=4,2; =3,4; ==0; .

F(4,2; 3,4)= 14,4.

Полученные решения проверены в MS Excel:

Введены параметры для поиска решения в созданной таблице (Рисунок 4)

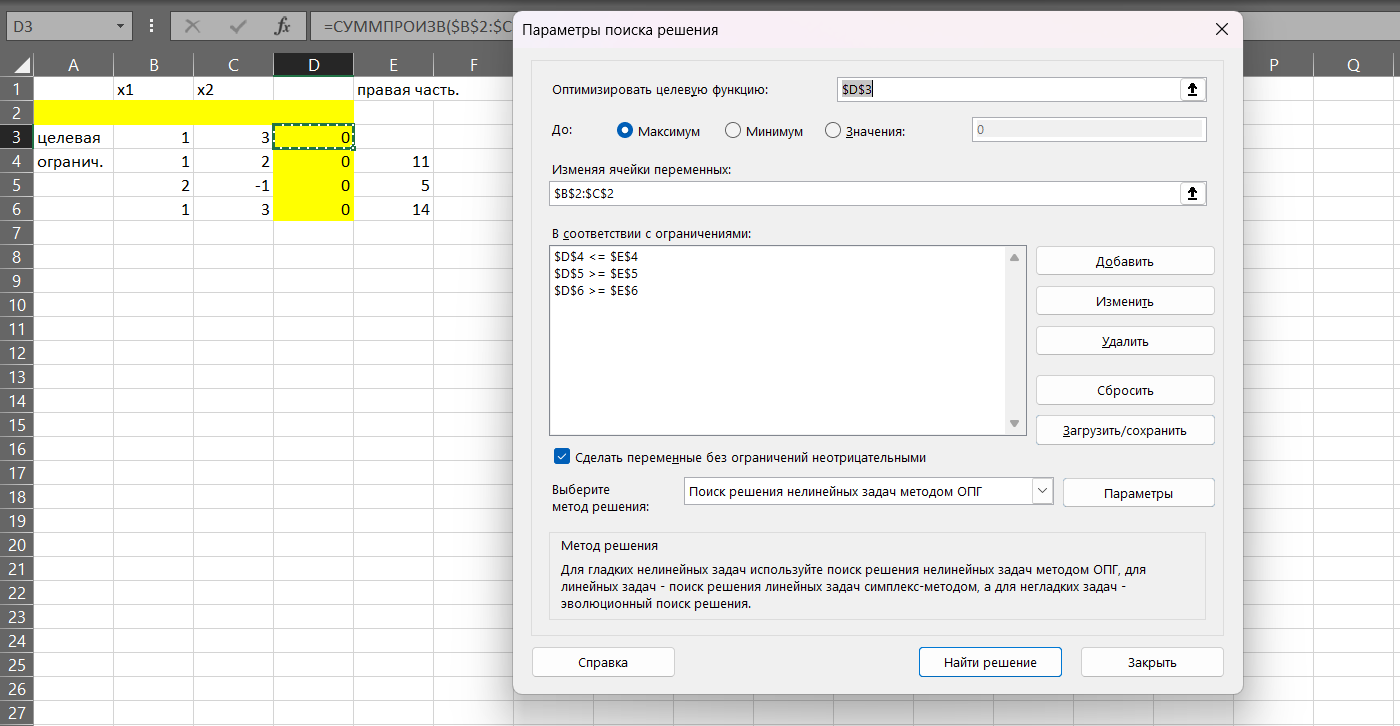
Рисунок 4- Настройка параметров поиска решений

Рисунок 5- Полученный результат

Составление двойственной задачи

Исходная задача

Ограничения:

Целевая функция:

В двойственной задаче переменных будет столько, сколько ограничений, т.е. каждое неравенство соответствует переменной.

Для проверки правильности составления двойственной задачи использован MS Excel (Рисунок 6-7)

Рисунок 6-Настройка параметров поиска решений

Рисунок 7- Полученный результат

На рисунке 7 видно, что двойственная задача составлена правильно.

Вывод: в лабораторной работе решена задача линейного программирования графическим методом и симплекс-методом, также выполнена проверка в MS Excel. Составлена двойственная задача исходной, решение задачи в MS Excel показало, что задача составлена правильно.

Список использованных источников:

1. Григорьева Н.Н., Яковлева Е.А. - Учебно-методическое пособие «Базовые математические методы и модели оптимизации »‒ ГУАП, 2023

2. Б. К. Акопян, Е. П. Виноградова, С. М. Герасимов, Н. Н. Григорьева - Учебно-методическое пособие «Прикладные методы оптимизации»‒ ГУАП, 2019