
Frisk_1_tom
.pdf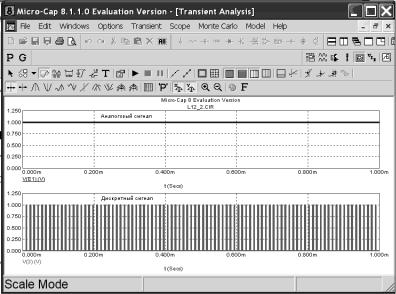
190 |
Глава первая. Описание лабораторных работ по ОТЦ |
|
|
виться окно Transient Analysis Limits. Запустите построение, нажав кнопку Run. На экране появиться графики аналогового и соответствующего ему дискретного сигнала (рис. 31).
Ðèñ. 31
Данные графики занесите в соответствующий раздел отчета.
4.3.3 Дискретизация аналогового экспоненциального сигнала
Для проведения дискретизации аналогового экспоненциального сигнала (рис. 3) вернитесь к исходной схеме, нажав на клавиатуре клавишу F3. Щелкните два раза на элементе Å1. В открывшемся окне NFV (рис. 15) нажмите кнопку Expand... .
В появившемся окне VALUE вместо 1 введите формулу аналогового сигнала exp(-4E3*t).
Закройте эти окна. Нажмите кнопки OK.
Построить график заданного аналогового и дискретного сигналов. Для этого в меню Analysis выберите команду Transient... (рис. 27). На экране появиться окно Transient Analysis Limits. Запустите построение, нажав кнопку Run.
На экране появиться графики аналогового и соответствующего ему дискретного сигнала.
Данные графики занесите в соответствующий раздел отчета.
4.3.4 Дискретизация аналогового двухполупериодного сигнала
Для проведения дискретизации аналогового двухполупериодного сигнала (рис. 4) вернитесь к исходной схеме, нажав на клавиатуре клавишу F3. Ùåëê-
Лабораторная работа ¹ 12 |
191 |
|
|
ните два раза на элементе Å1. В открывшемся окне NFV. (рис. 15) нажмите кнопку Expand... .
В появившемся окне VALUE вместо exp(-4E3*t) введите формулу аналогового сигнала abs(cos(2*pi*t*1E3)).
Закройте эти окна. Нажмите кнопки OK.
Построить график заданного аналогового и дискретного сигналов. Для этого в меню Analysis выберите команду Transient... (рис. 27). На экране появиться окно Transient Analysis Limits. Запустите построение, нажав кнопку Run.
На экране появиться графики аналогового и соответствующего ему дискретного сигнала
Данные графики занесите в соответствующий раздел отчета.
4.3.5 Дискретизация аналогового косинусоидального сигнала
Для проведения дискретизации аналогового косинусоидального сигнала (рис. 5) с частотой 1000 Гц (1Å3) вернитесь к исходной схеме, нажав на клавиатуре клавишу F3. Щелкните два раза на элементе Å1. В открывшемся окне NFV (рис. 15) нажмите кнопку Expand... .
В появившемся окне VALUE вместо abs(cos(2*pi*t*1E3)) введите формулу аналогового сигнала cos(2*pi*t*1E3).
Закройте эти окна. Нажмите кнопки OK.
Построить график заданного аналогового и дискретного сигналов. Для этого в меню Analysis выберите команду Transient... (рис. 27). На экране появиться окно Transient Analysis Limits. Запустите построение, нажав кнопку Run.
На экране появиться графики аналогового и соответствующего ему дискретного сигнала.
Сделайте вывод о возможности восстановления данного аналогового сигнала. Проверти выполнение теоремы Котельникова.
Данные графики занесите в соответствующий раздел отчета.
4.3.6 Эффект ложной частоты
Для наблюдения эффекта ложной частоты (рис. 11) увеличить частоту косинусоидального сигнала до 95 кГц (95Å3). Для этого вернитесь к исходной схеме, нажав на клавиатуре клавишу F3. Щелкните два раза на элементе Å1.
Âоткрывшемся окне NFV. (рис. 15) нажмите кнопку Expand... .
Âпоявившемся окне VALUE вместо cos(2*pi*t*1E3) введите cos(2*pi*t*95E3).
Закройте эти окна. Нажмите кнопки OK.
Построить график аналогового и дискретного сигналов (при f = 0,95fд). Для этого в меню Analysis выберите команду Transient... (рис. 27). На экране появиться окно Transient Analysis Limits. Запустите построение, нажав кнопку Run.
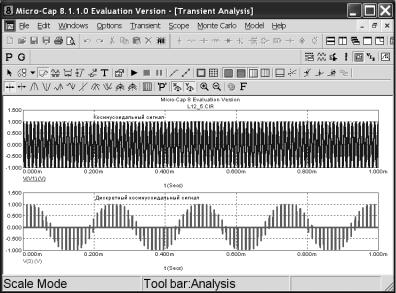
На экране появиться графики аналогового и дискретного сигнала (рис. 32). На нижнем графике отчетливо проявился эффект ложной частоты. Данные графики занесите в соответствующий раздел отчета.
Аналогично уменьшите частоту косинусоидального сигнала до 31 кГц (31Å3). Получите графики сигналов в этом случаи. Сделайте вывод о возмож-
192 |
Глава первая. Описание лабораторных работ по ОТЦ |
|
|
Ðèñ. 32
ности восстановления данного аналогового сигнала. Проверти выполнение теоремы Котельникова. Занесите данные графики в соответствующий раздел отчета.
5 Обработка результатов машинного эксперимента
Сравнить полученные данные с данными, полученными в предварительном расчете. Сделать выводы.
6 Вопросы для самопроверки
1.Какие системы называются дискретными?
2.Как происходит преобразование аналоговых сигналов в дискретные?
3.Что называют отсчетами?
4.Какую величину называют тактовыми моментами?
5.Почему интервал дискретизации нельзя выбрать произвольным об-
разом?
7 Содержание отчета
Отчет оформляется в формате MS Word. Шрифт Times New Roman 14, полуторный интервал.
Для защиты лабораторной работы отчет должен содержать следующий материал: титульный лист; цель работы; результаты машинного эксперимента;
Лабораторная работа ¹ 12 |
193 |
|
|
графики исследуемых зависимостей; выводы. К отчету должны быть приложены в напечатанном виде вопросы для самопроверки и ответы на них.
8Литература
1.Фриск В. В. Основы теории цепей. М.: РадиоСофт, 2002. 288 с.
2.Бакалов В. П., Дмитриков В. Ф, Крук Б. И. Основы теории цепей. М.: Радио и связь, 2003. 592 с.
3.Гольденберг Л. М., Матюшкин Б. Д., Поляк М. Н. Цифровая обработка сигналов. М.: Радио и связь, 1990. 256 с.
Лабораторная работа ¹ 13
Спектральный анализ сигналов
ñприменением ДПФ
1Цель работы
Ñпомощью программы Micro-Cap получить дискретные спектры различ- ных импульсных сигналов с использованием аппарата дискретного преобразования Фурье (ДПФ).
2 Задание для самостоятельной подготовки
Изучить основные положения теории цепей о дискретных сигналах стр. 276—277 [1], стр. 515—525 [2], стр. 8—20, 123—133 [3], 245—277 [4] и 187—204 [5]. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.
3 Предварительный расчет
3.1. Найти непрерывную спектральную плотность F(jω ) прямоугольного импульса (рис. 1)
|
|
U, 0 |
≤ t ≤τ |
|
|
u |
1 |
(t) = |
t |
> τ |
Â, |
|
|
0, |
|
||
где t — время;
τ = 1 мс — длительность импульса; U = 4 В — амплитуда импульса.
В формате Micro-Cap эта формула записывается так:
VALUME = 4*(t< = 1m)
Если неравенство в скобках истинно, то четверка умножается на 1. Если t таково, что неравенство в скобках ложно, то четверка умножается на 0.
Построить график модуля непрерывной спектральной плотности как функцию от частоты |F(jω )|.
3.2. Найти непрерывную спектральную плотность F(jω ) серии из трех прямоугольных импульсов показанных на рис. 2.
τ = 0,1 мс — длительность импульса;
Лабораторная работа ¹ 13 |
195 |
|
|
Ðèñ. 1 |
Ðèñ. 2 |
Т = 0,4 мс — период;
U = 1 В — амплитуда импульса.
Построить график модуля непрерывной спектральной плотности как функцию от частоты |F(jω )|.
3.3. Найти непрерывную спектральную плотность F(jω ) затухающей синусоиды (рис. 3)
|
|
−at |
sin(ω 1t), t ≥ 0 Â, |
u3 |
(t) = e |
|
|
|
0, |
t < 0 |
|
где t — время;
a = 800 1/с — коэффициент;
ω 1 = 8000 рад/c — угловая частота.
Ðèñ. 3
Построить график модуля непрерывной спектральной плотности как функцию от частоты |F(jω )|.
3.4. Найти непрерывную спектральную плотность F(jω ) прямоугольного радиоимпульса, образованного отрезком синусоиды (рис. 4).
sin(ω |
1t), 0 ≤ t ≤τ , |
u 4 (t) = |
0 > t > τ , |
0, |
|
ãäå ω 1 = 8000 рад/с — угловая частота; |
|
Ò1 = 2π /ω 1 — период синусоиды; |
|

196 |
Глава первая. Описание лабораторных работ по ОТЦ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 4
τ = nT1 — длительность импульса;
n = 3 — целое число периодов за время τ .
Построить график модуля непрерывной спектральной плотности как функцию от частоты |F(jω )|.
3.5. Найти непрерывную спектральную плотность F(jω ) серии из трех прямоугольных радиоимпульсов (из трех отрезков синусоид), показанных на рис. 5.
ω 1 = 8000 рад/с — угловая частота; Т1 = 2π /ω 1 — период синусоиды;
τ = nT1 — длительность импульса;
n = 3 — целое число периодов за время τ ; Ò = 4Ò1 — период.
Ðèñ. 5
Построить график модуля непрерывной спектральной плотности как функцию от частоты |F(jω )|.
4 Порядок выполнения работы
Непрерывная спектральная плотность (преобразование Фурье, интеграл Фурье) вычисляется по следующей формуле
∞
F(jω ) = ∫u(t)e − jω tdt,
−∞
ãäå F(jω ) — спектральная плотность;
Лабораторная работа ¹ 13 |
197 |
|
|
j= 
 −1 — мнимая единица;
−1 — мнимая единица;
ω— угловая частота;
t— время;
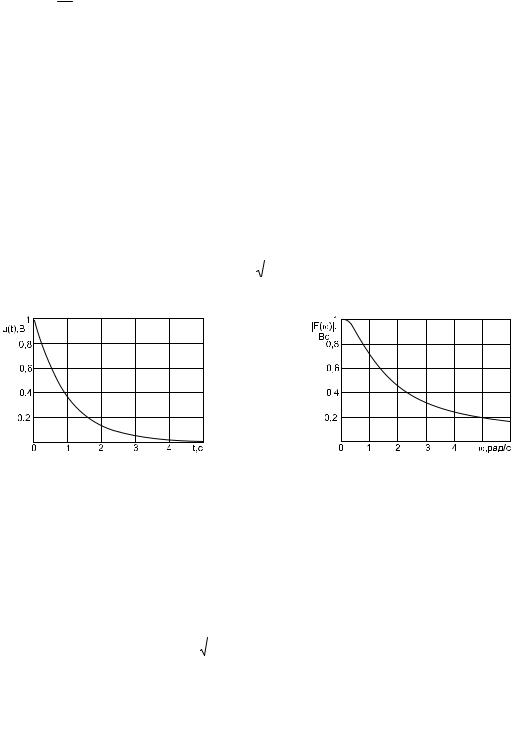
u(t) — абсолютно интегрируемый сигнал. Например, убывающая экспонента (рис. 6)
|
−t |
, t ≥ 0 Â. |
u(t) = e |
|
|
0, |
t < 0 |
|
Спектральная плотность этого сигнала будет равна
|
∞ |
|
|
∞ |
|
|
1 |
|
|
|
∫ |
|
|
|
∫ |
|
|
|
|
F(jω ) = |
u(t)e − jω tdt |
= |
|
e −te −ωj tdt = |
1 + jω |
. |
|||
|
−∞ |
|
|
0 |
|
|
|
||
Модуль непрерывной спектральной плотности как функцию от частоты |
|||||||||
буден равен |
|
|
|
|
|
|
|
|
|
|
|F(jω )| = |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
1 + ω 2 |
|
|
||||
|
|
|
|
|
|
|
|
||
Кривая |F(jω )| изображена на рис. 7.
Ðèñ. 6 |
Ðèñ. 7 |
Затухающая синусоида (рис. 3)
Спектральная плотность этого сигнала будет равна
|
∞ |
∞ |
|
ω |
2 |
2 |
|
|
∫ |
∫ |
|
|
|||
F(jω ) = |
u(t)− jω t dt = |
e |
−at sin(ω 1t)e −ωj tdt = |
(a + jω |
) +ω |
|
. |
|
−∞ |
0 |
|
1 |
|
Модуль непрерывной спектральной плотности как функцию от частоты буден равен
|
|F(jω )| = |
|
|
|
ω 1 |
|
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(a2 + ω 12 −ω 2 )2 + 4aω 2 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Отрезок синусоиды (рис. 4) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Спектральная плотность этого сигнала будет равна |
|
|
|
|
|
|
|
||||||||
|
∞ |
τ |
|
|
ω 1 |
|
|
|
|
|
− j |
ω |
n2π |
||
|
∫ |
|
∫ |
2 |
2 |
|
|
|
|
|
|
|
|||
F(jω ) = |
u(t)e − jω tdt = |
|
sin(ω |
1t)e −ωj tdt = |
(ω 1 |
−ω |
|
|
|
1 |
− e |
|
ω 1 |
. |
|
|
−∞ |
0 |
|
|
|
|
) |
|
|
|
|
||||
198 |
Глава первая. Описание лабораторных работ по ОТЦ |
|
|
Модуль непрерывной спектральной плотности как функцию от частоты (при ω 1τ = 2π n) буден равен
|
|
|
ω |
1 |
|
|
ω |
|
|
|F(jω |
)| = |
|
|
|
2sin |
|
|
nπ |
. |
|
|
|
|
||||||
|
|
|
ω 12 |
−ω 2 |
|
ω |
1 |
|
|
Серия из трех прямоугольных импульсов (рис. 2)
Спектральная плотность этого сигнала (по теоремам линейности и запаздывания) будет равна
F(jω ) = F1 (ωj )(1 + e − jω T + e − j2ω T ),
ãäå F1(jω ) — спектральная плотность первого импульса в пачке.
Эту же формулу можно применить и к серии из трех синусоид (рис. 5).
Дискретное преобразование Фурье (ДПФ)
В настоящее время большое значение придается цифровой обработке сигналов (ЦОС).
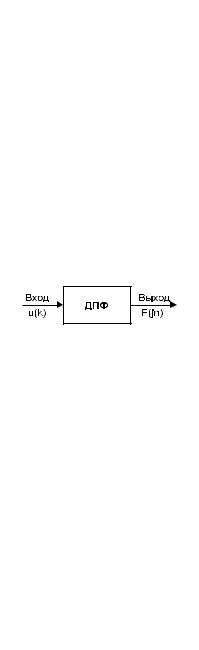
На практике вычисление спектральной плотности происходит с помощью цифровых вычислительных машин (рис. 8).
Ðèñ. 8
Поэтому сигнал представляют в виде конечного числа дискретных от- счетов.
Пусть сигнал представлен последовательностью из N отсчетов
u(k), 0 ≤ k ≤ N – 1.
Для того, чтобы из непрерывного сигнал u(t) получить отсчеты, нужно положить t = kT, где Т — интервал дискретизации во временной области (обычно эта величина постоянная и выбирается так, чтобы выполнялась теорема Котельникова); k = 0, 1, ..., N – 1 — целые числа.
Прямым дискретным преобразованием Фурье называют последовательность вида
N −1 |
− j |
2π |
|
F(jn) = ∑ |
|
nk |
|
u(k)e |
N , n = 0, 1, ..., N – 1. |
||
k=0
Обратным дискретным преобразованием Фурье называют последовательность вида
|
1 |
N −1 |
− j |
2π |
|
|
u(k) = |
∑ |
|
nk |
|||
F(jn)e |
N , k = 0, 1, ..., N – 1. |
|||||
|
||||||
|
N n =0 |
|
|
|
||
Определенные выше преобразования Фурье, не являются единственно возможными. На практике применяют и альтернативные преобразования Фурье.

Лабораторная работа ¹ 13 |
199 |
|
|
Пример. Рассчитаем ДПФ дискретного периодического сигнала, заданного на интервале своей периодичности шестью равноотстоящими отсчетами (N = 6)
u(k) = {1, 1, 1, 0, 0, 0}.
Этот дискретный сигнал (рис. 9) можно выразить с помощью следующей формулы
1 if
1 if u(k) =
1 if0 if
k = 0; k = 1; k = 2; k ≥ 3,
ãäå k = 0, 1, ..., 5.
Ðèñ. 9 Ðèñ. 10
В табл. 1 приведены результаты расчета ДПФ и его модуля (рис. 10).
k |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
u(k) |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
F(jn) |
3 |
1 – j1,732 |
0 |
1 |
0 |
1 + j1,732 |
|
|
|
|
|
|
|
|F(jn)| |
3 |
2 |
0 |
1 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получим ДПФ для различных сигналов, с помощью ЭВМ.
4.1 Запуск программы схемотехнического моделирования Micro-Cap
Включить ЭВМ и запустить программу Micro-Cap
C:\MC8DEMO\mc8demo.exe
èëè
ПУСК\Все программы\Micro-Cap Evaluation 8\Micro-Cap Evaluation 8.0.
