Добавил:

ILM Студент Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет им. М.В. Ломоносова

Предмет:

Математическая экономика

Файл:

ААВасин Математические_модели_рынков_и_аукционов

.pdf

Скачиваний:

Добавлен:

29.05.2024

Размер:

3.15 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 217 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Часть I

Доказательство теоремы 4.3. Из равенства		S ( p) S ( p)
вытекает, что	не существует производителей a , для которых
ca p Далее,	равенства S( p) V a D( p)	означают, что
	a ca p
спрос по цене	p будет удовлетворен полностью. Поэтому произ-
водитель a , для которого sa ca p ничего не продаст. Следо-
вательно, p(s ) p
1) Из условия следует, что D( p)( p ca ) D( p)( p ca ) при

p [ p M ] для всех производителей a , имеющих удельную себестоимость ca p Действительно, при p p из неравенства

D( p)( p c ) D( p)( p c )

получаем

D( p) p D( p) p c (D( p) D( p)) .

ОтсюдаD( p)( p ca ) D( p)( p ca ) .

Рассмотрим производителя a , такого, что ca p Ему невыгодно снижать цену s a p , поскольку он продаст весь свой объ-

ем V a и по цене p

Ему невыгодно выбирать и более высокую

цену sa p так как

(s s

) (s

)D(s

))

,V (s

(sa ca )D(sa )(1 Vp (s sa ) / D( p))

(sa ca )D(sa )(1

V b

V b )

b cb p b a

b cb p

(sa ca )D(sa )V a / D( p) ( p ca )V a ua (s ).

2)Предположим, что существует равновесие по Нэшу s Рас-

смотрим	производителя, имеющего удельную себестоимость
ca c p	При назначении новой цены sa p его прибыль

будет равна

Основные понятия, модели и результаты …

(s s

) (s

)D(s

))

,V (s s

(sa ca )D(sa )(1 Vp (s sa ) / D( p))

(sa ca )D(sa )V a / D( p) ( p ca )V a ua (s ).

При этом одно из последних двух неравенств выполнено как строгое. Следовательно, получено противоречие с тем, что ситуация s является равновесием по Нэшу.

Доказательство теоремы 4.4. Пусть выбраны va a A .

Функция предложения определяется этими объемами. Поэтому цена конкурентного равновесия p(v) зависит от вектора v . Как

отмечалось выше, на втором этапе удельные себестоимости мож-

но считать нулевыми. Поэтому цена p(v)		однозначно определя-
ется из условия D( p) va	(см. рис. 4.4). Условие e(D( p)) 1
a A
гарантирует выполнение	неравенства	D( p) p D( p) p при

p [ p M ] Поэтому все условия первой части теоремы 4.3 вы-

полнены. Из него вытекает, что в рассматриваемой подыгре существует единственное равновесие по Нэшу, соответствующее

ситуации s , для которой a A

s a p(v) Таким образом, пер-

вый этап эквивалентен модели Курно. Если же выполнены условия 2), то, согласно доказательству второй части теоремы 4.3, равновесия по Нэшу на втором этапе не существует ни при каком

выборе объемов va [0 V a ] .

Таким образом, в условиях первой части данной теоремы двухэтапная модель сводится к модели Курно. Для каких товаров выполнены эти условия? Для тех, спрос на которые эластичен, производство которых нельзя осуществлять по мере поступления заказов, и которые нельзя без значительных издержек долго хранить. В качестве примера отметим различные сельхозпродукты.

Часть I

5.Фирма<лидер в конкурентном окружении

идругие иерархические игры

Рассмотрим рынок с функцией спроса D( p) , на котором действует крупная фирма-лидер с функцией издержек C1(v) и много мелких фирм, характеризующихся суммарной функцией предложения S ( p) . Какова оптимальная стратегия фирмы-лидера?

Пусть взаимодействие происходит в условиях конкуренции по Бертрану–Эджворту, причем фирма-лидер первой назначает цену

и объем выпуска. При заданной стратегии ( p1,v1 ) прочие фирмы оказываются в условиях конкурентного рынка, то есть цена p и

объем выпуска определяются из условия								( p) D( p \| p1,v1)
объем выпуска определяются из условия							S	( p) D( p \| p1,v1)
баланса предложения			( p)	и остаточного спроса
баланса предложения		S	( p)	и остаточного спроса
1	1			D( p)		при		p p1
1	1								.
D( p \| p	,v )				v1	при		p p1	.
				D( p)	v1	при		p p1

Замечание. Данная функция остаточного спроса соответствует приоритету потребителей с высокими резервными ценами. Но найденные ниже оптимальные стратегии фирмы-лидера не зависят от этого предположения.

Как обычно, предполагается, что каждая фирма максимизирует свою прибыль. Покажем, что любая стратегия ( p1,v) , для ко-

торой p p1 , не является оптимальной. Действительно, послед-

нее неравенство означает, что фирма-лидер может продать тот же объем товара по более высокой цене. Поэтому оптимальна стратегия, для которой p p1, v1 D( p1) S( p1) . Задача поиска оптимальной стратегии фирмы-лидера принимает вид: найти

p1* max( p(D( p) S ( p)) C1(D( p) S ( p))).

То есть, задача полностью аналогична поиску оптимальной стратегии монополии (см. раздел 2), поскольку функция

Основные понятия, модели и результаты …

обладает всеми свойствами функции спроса.

D( p) D( p) S ( p)

В частности, оптимальная цена p1* p , где p – Вальрасовская цена. Найти p1* можно, построив функцию предложения Курно

для функции спроса ( p) .

Рассмотрим частный случай, когда D( p) max(0, D dp) , фирма-лидер и конкурентное окружение характеризуются постоянными предельными издержками c1, c2 и производственными мощностями V 1, V 2 . Если c2 c1 , то оптимальная цена и объем

*		*	), или
для фирмы-лидера определяются из условия: Sc ( p	) D( p

( p* c1)d = D dp v1 (см. рис. 5.1. а).

В случае c2 c1 также следует рассмотреть соотношение ос-

таточного спроса		(см.
	D( p) и функции предложения Курно Sc ( p)

рис. 5.1. б). Если их пересечению соответствует цена p* c2 , то

она определяет оптимальную стратегию, при этом конкурентное окружение не участвует в производстве.

Рисунок 5.1 а

Рисунок 5.1 б

При p* c2 (пересечение функций происходит на вертикальном участке функции остаточного спроса) оптимальный объем равен V1* min (V1, D dp* ) Sc1( p* ) . На практике для его реали-

Часть I

зации фирма-лидер назначает цену p* ( ) c2 , где 0 – ми-

нимальный шаг цены или минимальная скидка, которая дает возможность полностью продать предложенный объем. Конкурент-

ное окружение покрывает остаточный спрос D(c2 ) V1*. Наконец, при p* c2 для определения оптимальной страте-

гии необходимо сравнить соответствующую этой цене прибыль d ( p* c1)2 с прибылью при p1 c2 . Этот пример показывает, что

при разрывной функции остаточного спроса оптимальная стратегия не всегда соответствует ее пересечению с функцией предложения Курно.

В общем случае модели, учитывающие асимметрию состояний экономических агентов, их неравноправное положение, разрабатываются в рамках теории иерархических игр (в западной литературе их называют также моделями «принципал–агент»). Обсудим две таких модели.

Рассмотрим конфликтную ситуацию с двумя участниками, в которой первый игрок выбирает стратегии x из множества стратегий X , а второй – стратегии y из множества стратегий Y . Ин-

тересы	первого игрока характеризует функция выигрыша
F(x, y),	а второго – функция выигрыша G(x, y) . Они определены

на множестве всех ситуаций X Y . Каждый игрок стремится, по возможности, максимизировать свою функцию выигрыша.

Прежде, чем выбрать стратегии x X , y Y , первый игрок

(лидер, принципал) сообщает информацию о своем выборе второму игроку (агенту). Такого рода игры описывают взаимодействие между неравноправными игроками, например, между верхним и нижним звеньями управления в организации или фирме. Их называются иерархическими.

Решение по Гермейеру

Нас будет интересовать наилучший гарантированный результат (выигрыш), который может получить в игре первый игрок. Различные типы иерархических игр отличаются порядком ходов

Основные понятия, модели и результаты …

(т.е. выбором стратегий) и формой сообщений. Рассмотрим два основных варианта.

Игра 1 . Первый игрок выбирает стратегию x X и сообщает её второму. Затем второй игрок выбирает стратегию y Y , зная x .

Когда интересы игроков близки, смысл подобных сообщений в координации действий. Например, если вы решили с кемнибудь встретиться, то сообщаете, куда придете. В экономике игра типа 1 происходит, в частности, между регулирующим орга-

ном, который сообщает второму игроку (частной компании) установленную норму x (ставку налога, санитарную норму и т.п.). Второй игрок выбирает стратегию y выпуска и продажи, зная

норму x .

Найдем наилучший гарантированный результат первого игрока в игре 1 (решение по Гермейеру, см. Гермейер, 1976). Естест-

венно предположить, что	второй игрок, зная x,	выберет
y Y (x) Arg max G(x, y) ,	т.е. максимизирует свою	функцию
y Y

выигрыша G(x, y) . Первый игрок знает функцию выигрыша второго игрока и может найти множество Y (x) , но он не знает кон-

кретного выбора y Y (x). Величина W (x) min F(x, y) называ-

y Y ( x)

ется оценкой эффективности (гарантированным результатом) стратегии x. В общих предположениях множество Y (x) – непус-

тое и является компактом. Следовательно, минимум по y Y (x) достигается, и наилучший гарантированный результат имеет вид

F1 sup min F(x, y) .

x X y Y ( x)

Определение 5.1. Пусть задано 0 . Стратегия первого игрока x называется – оптимальной в игре 1 , если

W (x ) F1 .

Приведем пример, в котором супремум в выражении для F1

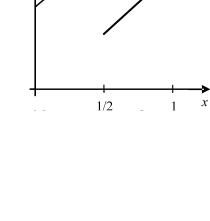
не достигается.	Пусть X Y [0,1] ,	F(x, y) 3x / 4 y / 2 ,
G(x, y) (x y)2 .

Часть I

3x		y	{1},	0 x 1/ 2;

1 : F1 sup min			, Y (x) {0,1},	x 1/ 2;
	4	2
0 x 1 y Y ( x)				1/ 2 x 1.
			{0},

График функции W (x) изображен на рисунке 5.2. Здесь F1 7 / 8 , x 1/ 2 4 / 3 - – оптимальная стратегия.

Рисунок 5.2

Решить игру 1 – значит найти величину F1 и оптимальную стратегию либо, если верхняя грань в выражении для F1 не дос-

тигается, – оптимальную стратегию x в зависимости от 0 . Игра 2 . Первый игрок перед выбором x имеет полную информацию о y . Он делает первый ход: сообщает второму игроку стратегию вида f :Y X , определяющую его действие в зави-

симости от действия второго игрока. Множество всех таких стратегий обозначим { f }. Например, менеджер может назначить ра-

ботнику оплату f ( y) в зависимости от объема произведенной

продукции.

Найдем выражение для наилучшего гарантированного результата первого игрока в игре 2 . Естественно предположить,

Основные понятия, модели и результаты …

что	второй	игрок, зная	f , выбирает y из множества
Y ( f ) Arg max G( f ( y), y) .			Рассмотрим следующие величины и
	y Y
множества:
	G2 max min G(x, y)		— наилучший гарантированный ре-
	y Y	x X

зультат второго игрока при условии, что первый применяет по

отношению		к	нему		стратегию	«наказания»:
f H :	f H ( y) Arg min G(x, y)			для любого y Y		;
		x X
	E Arg max min G(x, y)			– множество максиминных страте-
	y Y	x X
гий второго игрока;
D {(x, y) X Y \| G(x, y) G2};
	sup F(x, y), если D
					;
	K ( x, y) D		если D		;
	,		если D

	M min max F(x, y) .
	y E x X

Теорема 5.1 (теорема Гермейера). В данных предположениях наилучший гарантированный результат первого игрока в игре 2

равенF2 max[K , M ] .

Укажем стратегию первого игрока, обеспечивающую ему результат max[K, M ] . Рассмотрим два случая.

1) K M D . Для			всякого		0		найдется пара
(x , y ) D , такая, что F (x , y ) K . Положим
		x ,		если y y
						.
		f ( y)	Н ( y),	если y y		.
		f	Н ( y),	если y y

Покажем, что W ( f ) F (x , y ) K . Действительно, вто-
рой игрок, получив сообщение о				f ,	выберет y y , так как в
противном		случае	он		получит		выигрыш
G( f Н ( y), y) min G(x, y) G			G(x , y ) .
	x X	2
	x X

Часть I

1) K M . Укажем стратегию			f 0 , для которой	W ( f 0 ) M .
Положим
arg max F(x, y), еслиy E;
f 0	x X		еслиy E.
f Н		( y),	еслиy E.

Получив сообщение о		f 0 , второй игрок выберет		y E . Дей-

ствительно, если y E , то G( f H ( y), y) min G(x, y) < G2 . Отсюда

x X

W ( f 0 )

min

F( f *( y), y) min F( f *( y), y)

y Y*( f 0 )

y E

min max F (x, y) M .

y E x X

Докажем, что для произвольной стратегии f

выполнено не-

равенство

W ( f ) max[K, M ] .

Справедливо

неравенство:

def

( f )

supG( f ( y), y) max min G(x, y) G2 .

y Y

x X

Рассмотрим два случая. 1)

( f ) G2 . Тогда найдется страте-

гия второго

игрока

y0 ,

такая,

что G( f ( y0 ), y0 ) G , т.е.

( f ( y0 ), y0 ) D . Отсюда

W ( f )

inf

F( f ( y), y) F( f ( y0 ), y0 ) K max[K, M ] .

y Y*( f )

( f ) G2 .

Покажем, что

E Y *( f ) .

Действительно,

пусть y E . Тогда

G2 min G(x, y) G( f ( y), y)
	x X
Отсюда y Y ( f ) и E Y ( f ).
Итак,
W ( f ) inf	F( f ( y), y) inf F( f ( y), y)
y Y*( f )	y E

G( f ) G2 .

min max F(x, y) M . ▀

y E x X

Основные понятия, модели и результаты …

Решение по Штакельбергу

В предыдущем разделе расчет МГР и оптимальной стратегии как для 1 , так и для 2 , основан на предположении о выборе

вторым игроком наихудшей среди его оптимальных стратегий с точки зрения выигрыша первого игрока. Во многих реальных ситуациях первый игрок имеет возможность обеспечить благожелательный выбор партнера. Соответствующее решение называется решением по Штакельбергу (см. Васин, Морозов, 2005). В частности первый игрок может после игры осуществить платеж второму игроку в размере, зависящем от стратегии, реализованной последним. Формально это означает, что стратегия первого игрока включает компоненту z( y) 0 такую, что полные выигрыши

агентов имеют вид:

F (x, y, z( y)) F(x, y) z( y), G(x, y, z( y)) G(x, y) z( y).

За счет сколь угодно малого побочного платежа первый игрок может побудить партнера выбирать среди своих оптимальных стратегий наилучшую с точки зрения первого игрока. При этом

выражение для МГР в 1 принимает вид: F1 sup max F(x, y) , и

x X y Y ( x)

сложность расчета в общем случае не меняется, а выражение для МГР в игре 2 заметно упрощается.

Теорема 5.2. Наилучший результат первого игрока по Шта-

кельбергу в игре 2 равен		max	F(x, y) .
кельбергу в игре 2 равен	F2	max	F(x, y) .
		x , y: G( x ,y ) G max min G( x,y)
		y Y x X

Стратегия, обеспечивающая получение этой величины, имеет вид: если x*, y* реализуют указанный максимум, то x*( y* ) x*,

x* ( y) xН ( y) при y y* , z*( y) 0 при y y* .

Упражнение. Докажите эту теорему.

Важно подчеркнуть, что для реализации указанной стратегии необходимо выполнение основных условий игры Г2 : игрок-

лидер имеет физическую возможность реализовать любую аль-

<<< < Предыдущая 1 2 3 4 5 67 / 217 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>