MSCPATRAN2014
.PDF
Рис. 7.2. Геометрическая модель пластины в MSC.Patran.
3. Разбиение геометрической модели на конечные элементы.
Полученная геометрическая модель будет разбита на трехмерные конечные элементы типа Hex8 (рисунок 7.4).
Разбиваем ребра каждого слоя на необходимое нам количество одномерных элементов, чтобы в дальнейшем построить по ним конечно-элементную модель пластины. Четыре ребра слоя меньшей толщины разбиваем на 2 элемента указав в Elements|Create|Mesh Seed|Uniform в поле Number of Elements “Number = 2”, и в поле Curve List выбрав необходимые ребра. Аналогичным образом разбиваем на 4 элемента ребра слоя большей толщины указав в поле Number of Elements “Number = 4”. Получаем восемь ребер, разбитых на одномерные конечные элементы (рис 7.3).
Рис. 7.3. Ребра пластины разбитые на одномерные конечные элементы.
Теперь разбиваем всю пластину на трехмерные конечные элементы
Elements|Create|Mesh|Solid выбрав тип элемента Hex8 (Element Topology: Hex8), при этом значение длины конечных элементов в поле «Global Edge Length» укажем равное 1. Как видно из рис. 7.4 каждый слой был разбит на количество трехмерных элементов, соответствующее разбиению ребер на одномерные конечные элементы и соответственно длине пластины, в зависимости от величины в поле «Global Edge Length». Каждый прямоугольник - это сторона отдельного трехмерного элемента. В процессе разбиения могли возникнуть общие узлы, поэтому объединим их при помощи команды Elements|Equivalence.
71
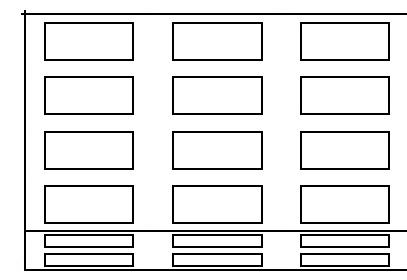
Рис. 7.4. Трехмерная конечно-элементная модель пластины в поперечном сечении.
4. Задание граничных условий и приложение нагрузок.
Поскольку рассматривается только распределение температур в пластине, достаточно только задать температуры, воздействующие на пластину. Задаем температуры
Loads/BC|Temp(Thermal)|Nodal|InputData в поле Boundary Temperature указав температуры нижней поверхности пластины: 70. Для верхей поверхности аналогичным образом указываем температуру: -30.
5. Моделирование материалов..
Зададим используемые материалы Materials|Isotropic|Manual Input|Input Properties
указав теплопроводность в поле Thermal Conductivity, для германия: 60,2 Вт/(м·К)
, для припоя 50 Вт/(м·К). Данных свойств будет вполне достаточно для проведения расчета.
6. Задание свойств конечных элементов.
Пластина состоит из двух слоев, каждый слой изготовлен из соответствующего материала. Присвоим слоям свойства материалов, заданных в п.5. Материал задается в меню Properties|Create|3D|Solid в поле ввода <Material Name>, где необходимо выбрать приготовленную ранее модель материала (германий или припой).
7. |
Процессорная обработка модели в MSC.Nastran и передача результатов для |
|||||
|
обработки постпроцессором. |
|
|
|
|
|
Расчет |
производится |
нажатием |
кнопки |
«Аpply» |
в |
меню |
Analysis|Analys|EntireModel|FullRun. При этом предварительно необходимо задать в
подменю SolutionType тип расчета: Steady State Analysis. |
|
|
|||
Подключение результатов для их визуализации постпроцессором |
MSC.Patran |
||||
производится |
нажатием |
кнопки |
«Аpply» |
в |
меню |
Analysis|AccessResults|AttachXDB|ResultsEntities.
8.Постпроцессорная обработка. Вывод результатов статического расчета моделей.
72

Рис. 7.5. Графическое представление температур биметаллической пластины.
Распределение температур в биметаллической пластине отобразим градиентной заливкой. Для получения градиентной заливки в меню Results|Create|Fringe выберем
Temperatures.
7.4. Содержание отчёта
Конечный результат имеет вид аналогичный представленному на рисунке 7.5. Окно результатов необходимо сохранить и предоставить преподавателю в отчете по работе.
7.5.Вопросы для самопроверки
1.Какие геометрические модели строились в данной работе
2.Каким методом происходило построение геометрической модели
3.Какие основные типы конечных элементов применялись
4.В какой системе единиц задавались геометрические размеры и нагрузка модели
5.Какой тип анализа использовался в данной работе
6.Какой вид нагрузки применялся
7.Перечислите основные этапы компьютерного решения задачи в
MSC.Patran|Nastran
73
Лабораторная работа 8. Расчет деформации биметаллической пластины под воздействием температуры.
8.1. Цель работы
Рассчитать деформацию биметаллической пластины под воздействием разности температур в среде MSC.Patran/Nastran, используя результаты расчета лабораторной работы 7.
8.2. Описание объекта исследования
Данная лабораторная работа использует результаты лабораторной работы №7. Необходимо отметить, что величины температуры, которые формируют выходные данные теплового анализа могут впоследствии использованы в качестве нагрузок в других типах анализа, например, таких как структурный анализ. Использование выходных величин в качестве нагрузок поддерживается в MSC.Patran посредством таблиц, известных как конечно-элементные поля (FEM fields). Эти таблицы базируются на предыдущих результатах анализа. Хорошим примером этого, является использование результатов теплового расчёта конструкции, и затем использование их для определения тепловых нагрузок в прочностном расчёте. Для того чтобы создать FEM Field необходимо вывести на дисплей требуемые результаты теплового расчёта, затем выделить на экране необходимые свойства и поместить их в таблицу.
8.3. Порядок выполнения работы.
Перед выполнением этой лабораторной работы необходимо выполнить предыдущую лабораторную работу №7: ” Термический анализ биметаллической пластины”. В первую очередь необходимо изменить тип анализа Preference|Analysis меняем Analysis Type, вместо Thermal ставим
Structural, так как будем проводить расчет деформации.
4. Задание граничных условий и приложение нагрузок.
Первые три пункта создания модели пропускаем, так как они уже были выполнены в предыдущей работе. Переходим сразу к заданию граничных условий и приложению нагрузок. Воспользуемся результатами теплового расчета для создания тепловых нагрузок:
Fields|Create|Spatial|FEM, вводим название Field Name: t_load, указываем FEM Field Definition: Continuous, Field Type: Scalar, Mesh/Results Group Filter: Current Viewport, Select Group: default_group (рис 8.1).
74

Рис. 8.1. Окно Fields.
Создаем блок нагрузок (Load Cases) для задания всех приложенных нагрузок: Load Cases|Create указав название блока (Load Case Name:struct_load) и его тип (Load Case Type:Static) (рис. 8.2). Блоки нагрузок (Load Cases) позволяют создавать группы нагрузок для различных расчетов. Например можно задать несколько блоков с различным численным значением нагрузки, и уже при анализе подключать необходимый блок, а не менять уже заданную нагрузку в Loads/BC.
75

Рис. 8.2. Окно Load Cases.
Задаем температуру: Load/BCs|Create|Temperature|Nodal, указываем тип анализа (Analysis Type: Structural), выбираем блок нагрузок (Current Load Case: struct_load), вводим название (New Set Name: temp_load) в
разделе Input Data в поле Temperature вводим f:t_load. Также жестко закрепляем 4 угловые точки основания пластины.
Затем переходим во вкладку Load Cases в списке существующих блоков выбераем наш (struct_load) и нажимаем кнопку Input Data. В появившемся окне в списке справа выбираем struct_load, в левом списке
76
выбираем нагрузки, которые подключаем к нашему расчету. По центру отображаются подключенные нагрузки. Нажимаем ОК, затем Apply.
5. Моделирование материалов.
Используемые материалы нужно задать заново, так как изменился тип анализа. Задаем свойства припоя: Materials|Isotropic|Manual Input|Input Properties указав модуль упругости, коэффициент Пуассона, коэффициент расширения и исходную температуру в полях Elastic Modulus: 1.3e7,
Poisson Ratio: 0.4, Thermal Expan. Coeff: 2.47e-5, Reference Temperature: - 30. Аналогичным образом задаем свойства германия:
Materials|Isotropic|Manual Input|Input Properties указав модуль упругости,
модуль сдвига, коэффициент расширения и исходную температуру в полях
Elastic Modulus: 1.3e7, Shear Modulus: 0.933e7, Thermal Expan. Coeff: 2.47e- 5, Reference Temperature: -30.
6. Задание свойств конечных элементов.
Присваиваем свойства материалов соответственным слоям. Перезаписывая старые значения.
7. Процессорная обработка модели в MSC.Nastran и передача
результатов для обработки постпроцессором.
Расчет производится нажатием кнопки «Аpply» в меню
Analysis|Analys|EntireModel|FullRun. При этом предварительно необходимо задать в подменю SolutionType тип расчета: Linear Static, в подменю Subcase Select выбрать созданный блок нагрузок struct_load.
Подключение результатов для их визуализации постпроцессором MSC.Patran производится нажатием кнопки «Аpply» в меню
Analysis|AccessResults|AttachXDB|ResultsEntities.
8.Постпроцессорная обработка. Вывод результатов статического расчета моделей.
77

Рис. 8.3. Графическое представление продеформированной биметаллической пластины.
Отобразим результаты статического расчета в виде градиентной (цветовой) заливки модели объекта в соответствии с деформированием.
Для этого в меню Results|Create|Fringe выберем DisplacementTranslational.
8.4. Содержание отчёта
Конечный результат имеет вид аналогичный представленному на рисунке 7.5. Окно результатов необходимо сохранить и предоставить преподавателю в отчете по работе.
8.5.Вопросы для самопроверки
1.Какие геометрические модели строились в данной работе
2.Каким методом происходило построение геометрической модели
3.Какие основные типы конечных элементов применялись
4.Какой тип анализа использовался в данной работе
5.Какой вид нагрузки применялся
6.Какие способы задания нагрузки применялись
7.Что такое Load Case
8.Что такое FEM fields
9.Почему FEM fields пременялись в данной работе
78
ЛИТЕРАТУРА
1. С.П. Рачков NASTRAN для Windows.— М.:НТП 2004. — 552 с.
2.Е.К.Рыбников, С.В.Володин, Р.Ю. Соболев Инженерные расчёты механических конструкций в системе Patran-Nastran. Часть I.
Учебное пособие – М., 2003. — 130 с.
3.Е.К.Рыбников, С.В.Володин, Р.Ю. Соболев Инженерные расчёты механических конструкций в системе Patran-Nastran. Часть II.
Учебное пособие. – М., 2003. — 174 с.
4.Д.Г. Шимкович Расчет конструкций в . NASTRAN – М.:ДМК, 2004.
— 704 с.
5.В.И.Феодосьев Сопротивление материалов— Изд. 13— е, стер .— М.: Издательство МГТУ им. Н. Э. Баумана, 2005 .— 590,
6.Агамиров, Л.В. Сопротивление материалов. Краткий курс [Текст]: для студентов вузов / Л. В. Агамиров .— М.: АСТ: Астрель, 2003 .— 256 с
7.Введение в сопротивление материалов / П. А. Павлов, Л. К. Паршин, Г. Б. Колчин, Б. Е. Мельников; под ред. Б. Е. Мельникова ; Санкт-
Петербургский государственный технический университет .— Изд. 2-е, исп.— СПб.: Издательство "Лань", 2002 .— 155 с
8.В.Г. Мельников, С.Е. Иванов, Г.И. Мельников. Компьютерные лабораторные работы в системе инженерного анализа - СПб: НИУ ИТМО, 2012. – 74 с.
9.В. Г. Мельников, С. Е. Иванов, Г. И. Мельников. Компьютерные
технологии в механике приборных систем / Под ред. В. Г. Мельникова.— СПб.: СПбГУ ИТМО, 2006 .— 130 с.
10.В.Г. Мельников, С.Е. Иванов, Г.И. Мельников, А.Г.Кривошеев Компьютерные лабораторные работы по сопротивлению материалов” - СПб: СПбГУ ИТМО, 2010. – 60 с.
11.А.А.Хмелев, В.А. Сидоров Сопротивление материалов. Лаб.работы – Мн.:УП 2004. —206 с.
79

В 2009 году Университет стал победителем многоэтапного конкурса, в результате которого определены 12 ведущих университетов России, которым присвоена категория «Национальный исследовательский университет». Министерством образования и науки Российской Федерации была утверждена программа его развития на 2009–2018 годы. В 2011 году Университет получил наименование «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики»
КАФЕДРА ТЕОРЕТИЧЕСКОЙ И ПРИКЛАДНОЙ МЕХАНИКИ
В1900 году Государственный Совет России принял решение о создании в Ремесленном училище цесаревича Николая механикооптического и часового отделения. Именно из этого отделения за прошедшие 100 лет вырос Санкт-Петербургский государственный институт точной механики и оптики (технический университет).
Курсы механики преподавались в Университете с самого начала его основания. В Российской национальной библиотеке Санкт-Петербурга хранится руководство по теоретической механике для учащихся IV класса Петербургского Ремесленного училища цесаревича Николая 1900 года издания.
При создании на базе механико-оптического и часового отделения сначала техникума, а затем института точной механики и оптики, уровень преподавания теоретической механики естественно повышался. В результате этого в начале 1930-х годов в институте была создана кафедра теоретической механики.
В1940-х годах ее возглавлял профессор, доктор физикоматематических наук Н.И. Идельсон. Одновременно он был также заведующим кафедрой гироскопии и гироскопических приборов ЛИТМО, что свидетельствует о широкой области его научных интересов и научных исследований на обеих кафедрах.
В1950-х годах кафедру возглавил доцент ( а затем профессор ) Г.Д. Ананов (1916-1976). Он был известным специалистом в области графоаналитических методов и применял их к исследованию сложных пространственных механизмов и к решению задач астронавигации, Георгий Давидович также увлеченно занимался программированным обучением и внедрением технических средств в учебный процесс.
80
