MSCPATRAN2014

Лабораторная работа 6. Оптимизация топологии скобы.

6.1.Цель работы

При проектировании модели выполняется оптимизация топологии, чтобы сгенерировать концептуально новую модель проекта с учетом задачи оптимизации массы и калибровки формы при удовлетворении всех ограничений и условий внешних воздействий в проекте.

6.2.Описание объекта исследования

Рассматривается модель скобы, выполняется оптимизация топологии модели, создается новая форма скобы, при снижении обшей массы и сохранении прочностных характеристик.

Вработе исследуется модель стальной ручки (скобы),

61

материал сталь.

6.3.Порядок выполнения работы.

В работе выполняется моделирование скобы, геометрии, материала, нагрузок и ограничений в системе инженерного анализа MSC.Patran.

Выполняется оптимизация топологии модели, создаются новые формы скобы, при снижении обшей массы на 40% и сохранении прочностных характеристик модели.

1.Выбор системы единиц измерения.

Вкачестве согласованной системы единиц будем применять систему, обозначаемую в MSC.Patran как «SI (mm-N-Ton)», что означает систему (мм-Н-т), при этом силы будут исчисляться в Ньютонах, длинны - в миллиметрах.

2.Построение геометрической модели объекта.

Проводится построение трехмерной модели пластины.

Для построения трехмерной модели воспользуемся библиотекой примитивов MSC.Patran (Geometry|Create|Solid|Primitive). Построим трехмерную модель с началом в нуле глобальной системы отсчета. Для этого создадим два геометрических примитива и выполним вычитание одного из другого и в результате получим единое твердое тело.

Геометрическая модель скобы представлена на рисунке 1.2

Рис 6.2. Трехмерная геометрическая модель скобы в MSC.Patran

62

Далее отобразим результаты оптимизации и генерации новой формы скобы. Мы получили новую форму скобы, уменьшили массу скобы на 40% при сохранении прочностных характеристик.

Выберем в поле Action - Display Result, для Select Result Case выберем результат DESIGN CYCLE и отметим Fringe.

Рис 6.7. Результаты генерации новой формы скобы.

Для проверки прочностных характеристик новой сгенерированной модели скобы можно выполнить анализ оптимальной конечно-элементной модели скобы.

6.4.Содержание отчёта

Отчет должен содержать все исходные параметры модели оптимизации скобы в соответствии с номером варианта и копию окна результата оптимизации модели скобы в среде MSC.Patran.

Конечный результат имеет вид аналогичный представленному на рисунке.. Окно результатов необходимо вставить в отчет и предоставить преподавателю.

Рис 6.8. Конечно-элементная модель скобы для отчета

67

6.5.Вопросы для самопроверки

1.Какие критерии используются при решении задачи оптимизации?

2.Приведите основные методы, применяемые для решения задач оптимизации.

3.Какие логические операции можно выполнять с геометрическими примитивами?

4.Какие трехмерные примитивы применяются при моделировании?

5.Какие свойства необходимо задать для модели?

6.Какие виды конечных элементов можно применить для данной модели?

7.Какие параметры оптимизации были установлены в данной задаче?

8.Приведите тип решателя для задачи оптимизации?

9.Какие методы применяются в Nastran для оптимизации?

10.Какие библиотеки включает в себя Patran?

11.Какие виды анализа возможно выполнять в Nastran?

12.С какими системами возможно связать Patran?

13.Какие виды геометрических моделей возможно построить в Patran?

14.Для чего применяется автоматическое построение сетки конечных элементов модели?

15.В каких форматах возможен импорт и экспорт геометрической модели

?

16.Каким образом используются результаты расчёта системы Nastran?

17.В чем отличие линейного анализа от нелинейного?

18.В каком методе применяется матрица жесткости?

19.Зачем выполняют оптимизацию сетки конечных элементов модели?

20.Какие виды оптимизации возможно выполнить в Nastran?

68

Лабораторная работа 7. Термический анализ биметаллической пластины.

7.1. Цель работы

Провести анализ температурной нагрузки в биметаллической пластины в среде

MSC.Patran/Nastran.

7.2.Описание объекта исследования

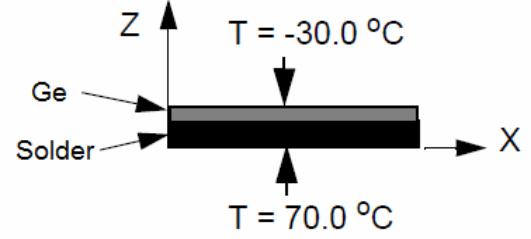
Вработе исследуется пластина размером 2.5 см на 2.5 см и толщиной 2 см, состоящая

из двух слоев: слой из припоя (Solder) толщиной h1 и слой из германия (Ge) толщиной h2. Верхнюю поверхность слоя германия имеет температуру -30оС, нижняя поверхность слоя припоя температуру 70оС (рис. 7.1). Задача определить распределение температур с помощью статического анализа.

Рис. 7.1. Схема поперечного сечения пластины.

В таблице 7.1. приведены толщины слоев h1 и h2 в соответствии с номером варианта.

69

Таблица 7.1. Толщина слоев по вариантам

7.3.Порядок выполнения работы.

Вработе используется термальный тип анализа, поэтому после создания новой базы данных необходимо выбрать тип анализа - Analysis Type: Thermal.

1.Выбор согласованной системы единиц измерения.

Вработе применяется согласованная система единиц «SI (mm-N-Ton)»: силы задаются в Ньютонах, длинны - в миллиметрах, нормальное напряжение s и модуль Юнга E - в мегапаскалях (МПа).

2.Построение геометрической модели объекта.

Для начала построим основную поверхность в плоскости XY с началом в нуле глобальной системы отсчета (Geometry|Create|Surface|XYZ). Для этого в поле Vector Coordinates List укажем размеры поверхности в миллиметрах <25 25 0>, а в поле Origin Coordinates List точку начала [0 0 0]. Затем по созданной поверхности методом выталкивания построим трехмерную твердотельную модель первого слоя

(Geometry|Create|Solid|Extrude), в поле Translation Vector указав расстояние и направление выталкивания в соответствии с вариантом <0 0 h1>, указав Solid Type: Isomeshable, в поле Surface List выбрав созданную поверхность Surface 1. Аналогичным образом создаем второй слой нажав на пиктограмму Solid Face и выбрав поверхность

Solid 1.6 (Surface List: Solid 1.6), в поле Translation Vector указав толщину второго слоя

<0 0 h2>. В результате получаем геометрическую модель биметаллической пластины состоящую из двух твердотельных трехмерных объектов Solid 1 и Solid 2 (рис. 7.2).

70