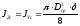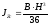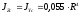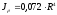Практика сопромат
.docxПрактическое занятие 1.1
Расчет статически неопределимых стержней при растяжении (сжатии).
Статически
неопределимыми называются такие
конструкции, в элементах которых при
помощи только одних уравнений статики
определить усилия невозможно. Например,
на рис.1.1 показан ступенчатый стержень,
жестко закрепленный в точках
 и
и
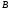 .
На стержень действуют силы
.
На стержень действуют силы
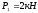 и
и
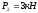 .
Модуль продольной упругости материала
стержня
.
Модуль продольной упругости материала
стержня
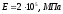 .
Площади поперечных сечений участков:
.
Площади поперечных сечений участков:
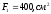 ;
;
 ;
;
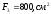 .
Длина участка
.
Длина участка
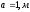 .
Необходимо раскрыть статическую
неопределимость, определить продольные
усилия, возникающие в различных частях
стержня, нормальные напряжения и
перемещения различных точек стержня
при заданной нагрузке.
.
Необходимо раскрыть статическую
неопределимость, определить продольные
усилия, возникающие в различных частях
стержня, нормальные напряжения и
перемещения различных точек стержня
при заданной нагрузке.
Заменим
действие опор на стержень реакциями (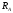 и
и
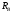 )
и составим уравнение проекций сил на
ось стержня (ось
)
и составим уравнение проекций сил на
ось стержня (ось
 ):
):
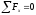 ;
;
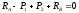 , (1.1)
, (1.1)

Рис. 1.1
Остальные
уравнения статики дадут нам такое же
выражение (1.1). В одно уравнение входят
два неизвестных усилия (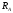 и
и
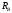 ),
следовательно, задача один раз статически
неопределима.
),
следовательно, задача один раз статически
неопределима.
Для расчета таких систем необходимо использовать уравнения, содержащие деформации элементов конструкций. Так как концы стержня жестко закреплены, то общая длина не изменяется:
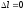 .
.
Общая деформация стержня будет складываться из деформаций его элементов:
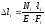 ,
(1.2)
,
(1.2)
где
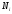 – продольное усилие на
– продольное усилие на
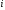 -том
участке;
-том
участке;
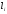 – длина
– длина
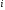 -
того участка;
-
того участка;
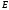 – модуль продольной упругости материала;
– модуль продольной упругости материала;
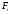 – площадь поперечного сечения
– площадь поперечного сечения
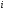 -
того участка.
-
того участка.
Выразим
продольные усилия в поперечных сечениях
стержня через одну из неизвестных
реакций
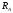 .
.
Разделим стержень на участки по местам приложения сосредоточенных нагрузок и местам изменения поперечного сечения стержня. Для приведенной схемы получаем три участка (рис. 1.1).
Мысленно
рассечем первый участок произвольно
взятым поперечным сечением и отбросим
нижнюю часть балки, заменяя ее действие
на верхнюю часть продольной силой
 ,
которую первоначально направляем в
сторону растяжения рассматриваемого
элемента первого участка (рис. 1.2).
,
которую первоначально направляем в
сторону растяжения рассматриваемого
элемента первого участка (рис. 1.2).
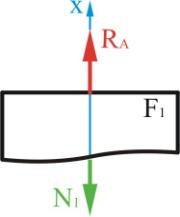
Рис. 1.2
Из
условия равновесия: 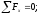
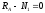 ;
;
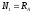 (1.3)
(1.3)
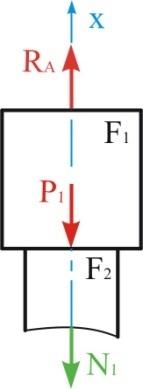
Рис. 1.3
Мысленно
рассечем второй участок произвольно
взятым поперечным сечением и отбросим
нижнюю часть балки, заменяя ее действие
на верхнюю часть продольной силой
 которую первоначально направляем в
сторону растяжения рассматриваемого
элемента первого участка (рис. 1.3).
которую первоначально направляем в
сторону растяжения рассматриваемого
элемента первого участка (рис. 1.3).
Из
условия равновесия:
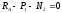 ;
;
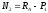 (1.4)
(1.4)
Для
третьего участка (рис. 1.3):
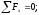
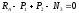 ;
;
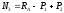 (1.5)
(1.5)
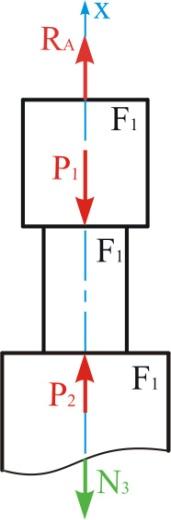
Рис. 1.4
Деформация участков согласно ф-ле (1.2):
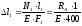 (1.6)
(1.6)
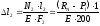 (1.7)
(1.7)
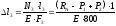 (1.8)
(1.8)
Общая деформация должна равняться нулю:

Умножив
обе части уравнения на
 получим:
получим:
 ,
,
или:
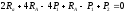
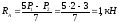 .
.
Из выражения (1.1):
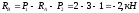 (1.8)
(1.8)
Знак
«-» указывает
на обратное направление реакции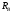 .
.
Определяем значения осевых усилий для каждого участка по найденным ранее выражениям (1.3.) – (1.5):
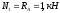 ;
;
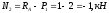 ;
;
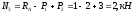 .
.
По
полученным значениям строим эпюру
осевых усилий. Для этого проводим нулевую
(базовую) линию параллельно оси стержня,
перпендикулярно которой будем в масштабе
откладывать значения осевых усилий
(рис. 1.1). В одну сторону откладываем
положительные значения, в другую -
отрицательные. Эпюра заштриховывается
перпендикулярно нулевой линии, а внутри
эпюры ставится знак откладываемой
величины. Рядом указываются значения
откладываемых величин. Рядом с эпюрой
в кавычках указывается название эпюры
(«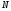 »)
и через запятую - единицы измерения (
»)
и через запятую - единицы измерения ( ).
).
Нормальные напряжения в поперечных сечениях:
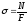 (1.8)
(1.8)
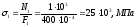 ;
;
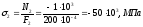 ;
;
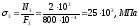 .
.
По
полученным значениям нормальных
напряжений строим эпюру нормальных
напряжений (« »)
(рис. 1.1).
»)
(рис. 1.1).
Определим деформацию каждого участка:
 ;
;
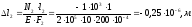 ;
;
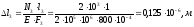 .
.
Эпюру
перемещений строим по перемещениям
точек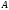 ,
,
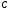 ,
,
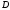 ,
,
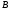 .
.
Сечение
в точке
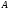 возьмем как базовое, перемещение которого
возьмем как базовое, перемещение которого
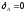 .
Тогда перемещение точки
.
Тогда перемещение точки
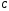 будет равно удлинению первого участка:
будет равно удлинению первого участка:
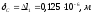
Перемещение
точки
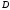 будет складываться из
перемещения точки
будет складываться из
перемещения точки
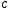 и удлинения второго участка:
и удлинения второго участка:
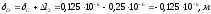
Перемещение
точки
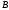 будет складываться из
перемещения точки
будет складываться из
перемещения точки
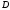 и удлинения второго участка:
и удлинения второго участка:
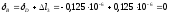
Перемещение
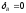 является своего рода проверкой
правильности решения данной задачи,
так как точка
является своего рода проверкой
правильности решения данной задачи,
так как точка
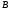 принадлежит
неподвижной опоре.
принадлежит
неподвижной опоре.
По
полученным значениям
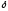 строим
эпюру перемещений («
строим
эпюру перемещений («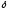 »)
(Рис. 1.1).
»)
(Рис. 1.1).
Так
как внутри участков перемещения
поперечных сечений имеют пропорциональную
зависимость от координаты сечения
 ,
значения, отложенные в точках
,
значения, отложенные в точках
 ,
,
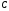 ,
,
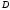 ,
,
 ,
соединяются между собой прямыми линиями.
,
соединяются между собой прямыми линиями.
Практическое занятие 1.2
Геометрические характеристики плоских сечений.
При определении положения главных осей и величин главных центральных моментов инерции сложного профиля, состоящего из простых частей можно руководствоваться следующим порядком:
-
провести произвольную систему прямоугольных координат. Разбить фигуру на простые части и определить положение ее центра тяжести;
-
провести начальную систему центральных осей
 ,
,
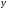 так, чтобы вычислить моменты инерции
частей фигуры относительно этих осей
было наиболее просто; определить
моменты инерции
так, чтобы вычислить моменты инерции
частей фигуры относительно этих осей
было наиболее просто; определить
моменты инерции
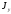 ,
,
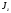 ,
,
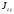 сложного сечения;
сложного сечения; -
определить угол наклона главных центральных осей;
-
определить значения главных центральных моментов инерции сложного сечения.
Рассмотрим плоское сечение, показанное на рис.1.
1.
Для заданного составного сечения выберем
произвольно систему координат
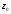 -
-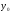 .
.
Лучше
всего проводить координатные оси так,
что бы они совпадали с главными осями
инерции составных площадей. Поскольку
сложное сечение условно можно разложить
на полукруглое сечение с радиусом
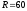 ,мм
и двутавровый профиль №22, ось
,мм
и двутавровый профиль №22, ось
 направим так, что бы она совпадала
с главной осью инерции полукруга, а ось
направим так, что бы она совпадала
с главной осью инерции полукруга, а ось
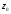 так, что бы она совпадала с главной осью
инерции двутаврового профиля.
так, что бы она совпадала с главной осью
инерции двутаврового профиля.
Положение центра тяжести полукруглого сечения по таблице 1:

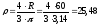 мм.
мм.
Положение центра тяжести двутаврового сечения определяется по сортаменту (Приложение 1 [i])
Координаты
центра тяжести полукруглого сечения
в системе координат
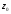 -
-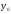 можно определить по рис 1
можно определить по рис 1
 мм;
мм; 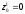 мм
мм
Координаты
центра тяжести двутаврового сечения
в системе координат
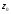 -
-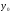 :
:
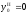 мм
мм 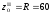 ,
мм
,
мм
Площадь полукруглого сечения:
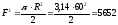 ,
мм2
,
мм2
Площадь двутаврового сечения берется из сортамента (Приложение 1 [1]):
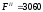 мм2
мм2
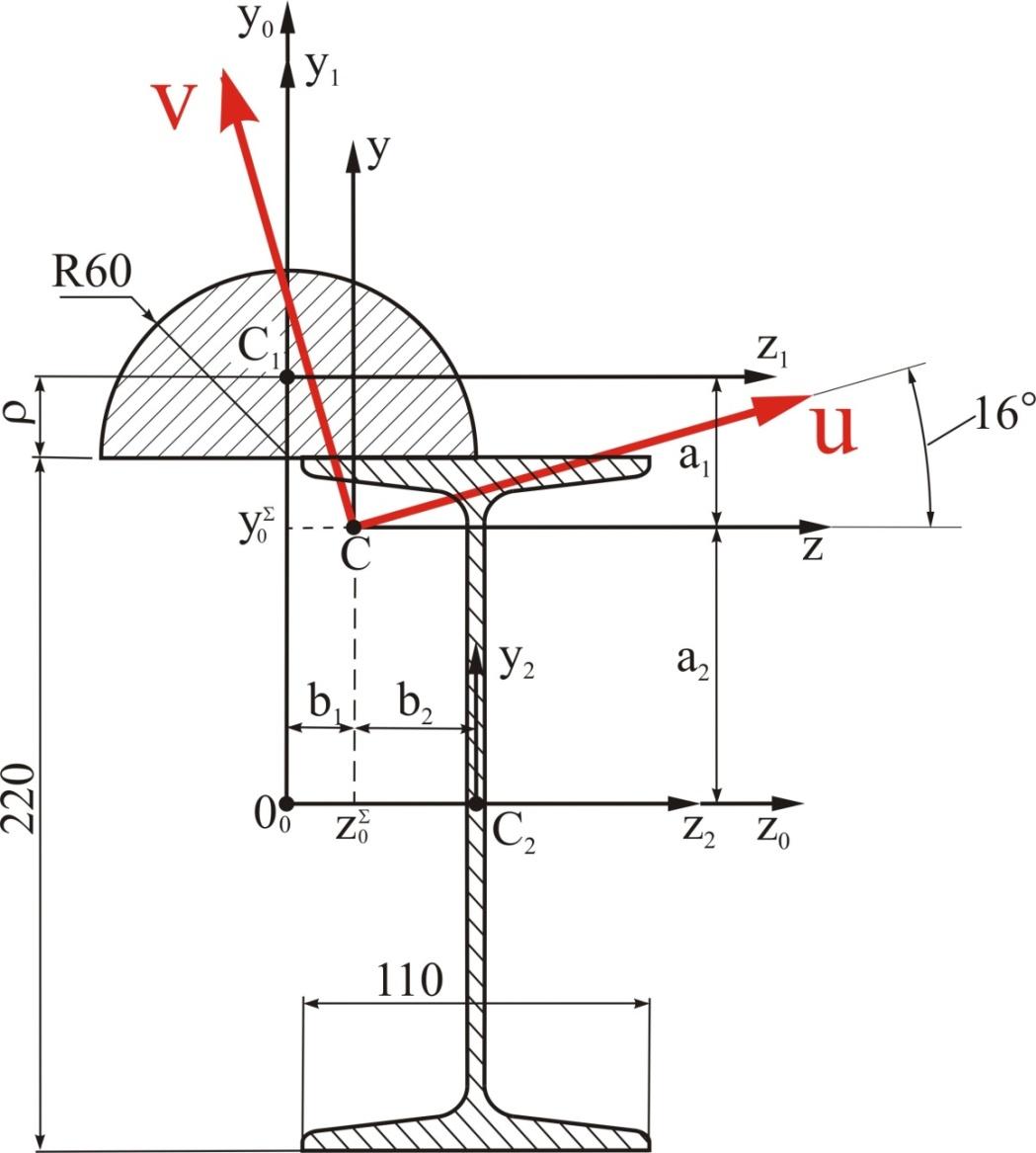
Рис. 2.6
Координаты
центра тяжести суммарного сечения в
системе координат
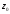 -
- ,
состоящего из полукруглого и двутаврового
сечения:
,
состоящего из полукруглого и двутаврового
сечения:
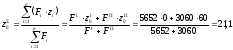 мм
мм
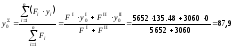 мм
мм
2.
Проведем начальную систему центральных
осей
 -
-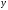 ,
параллельных главным
центральным осям полукруглого
и двутаврового сечений.
Моменты инерции
,
параллельных главным
центральным осям полукруглого
и двутаврового сечений.
Моменты инерции
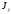 ,
,
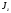 ,
,
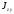 сложного сечения будем вычислять как
сумму моментов инерции полукруглого и
двутаврового сечений. Для этого сначала
запишем значение моментов инерций
данных сечений относительно их главных
центральных осей, а потом определим
моменты инерций этих сечений относительно
начальной системе центральных осей
сложного сечения будем вычислять как
сумму моментов инерции полукруглого и
двутаврового сечений. Для этого сначала
запишем значение моментов инерций
данных сечений относительно их главных
центральных осей, а потом определим
моменты инерций этих сечений относительно
начальной системе центральных осей
 -
- .
.
Осевой
момент инерции полукруглого сечения,
относительно главных центральных осей
полукруглого сечения
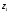 -
-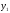 :
:
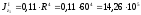 ,
мм4
,
мм4
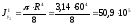 ,
мм4
,
мм4
Осевой
момент инерции двутаврового сечения
относительно его главных центральных
осей
 -
-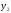 :
:
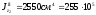 мм4
мм4
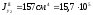 мм4
мм4
Центробежные моменты инерции полукруглого и двутаврового сечений относительно их главных осей инерций равны нулю:
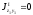 ,
мм4
,
мм4
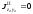 ,
мм4
,
мм4
Для определения осевых моментов инерции полукруглого и двутаврового сечений относительно начальных центральных осей, параллельных главным осям инерции каждого из сечений, найдем расстояния между соответствующими осями.
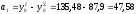 мм
мм
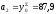 ,
мм
,
мм
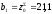 ,
мм
,
мм
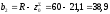 ,
мм
,
мм
Осевые моменты инерций полукруглого
и двутаврового сечений, относительно
начальных центральных осей суммарного
сечения
 ,
,
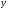 :
:
 ,
мм4
,
мм4
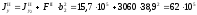 ,
мм4
,
мм4
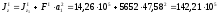 мм4
мм4
 мм4
мм4
Осевые моменты инерций суммарного
сечения, относительно начальных
центральных осей суммарного сечения
 ,
,
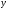
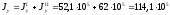 ,
мм4
,
мм4
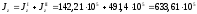 ,мм4
,мм4
Центробежные моменты инерции
полукруглого и двутаврового сечений
относительно центральных осей
суммарного сечения
 ,
,
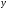
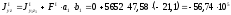 ,
мм4
,
мм4
 ,мм4
,мм4
Отметим, что координаты
 и
и
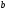 следует подставлять с учетом их знаков.
Центр тяжести полукруглого сечения
лежит в области отрицательных значений
следует подставлять с учетом их знаков.
Центр тяжести полукруглого сечения
лежит в области отрицательных значений
 в системе координат
в системе координат
 -
-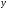 ,
поэтому значение величины
,
поэтому значение величины
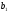 подставлено со знаком минус. Положение
центра тяжести двутавра лежит в
отрицательной области значений
подставлено со знаком минус. Положение
центра тяжести двутавра лежит в
отрицательной области значений
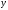 в системе координат
в системе координат
 -
-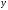 ,
поэтому значение величины
,
поэтому значение величины
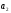 подставлено со знаком минус.
подставлено со знаком минус.
Центробежный момент инерции
суммарного сечения относительно
начальных центральных осей
 ,
,

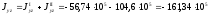 ,
мм4
,
мм4
3. Угол наклона главной центральной
оси
 суммарной площади к начальной центральной
оси
суммарной площади к начальной центральной
оси
 определится из зависимости
определится из зависимости
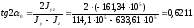
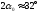
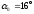
Проведем главные центральные оси составного сечения
4. Главные центральные моменты инерции суммарного сечения

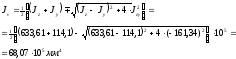
Т. к.
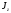 >
>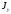 ,
принимаются верхние знаки:
,
принимаются верхние знаки:
Главные центральные радиусы инерции
 мм;
мм;
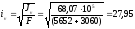 мм
мм
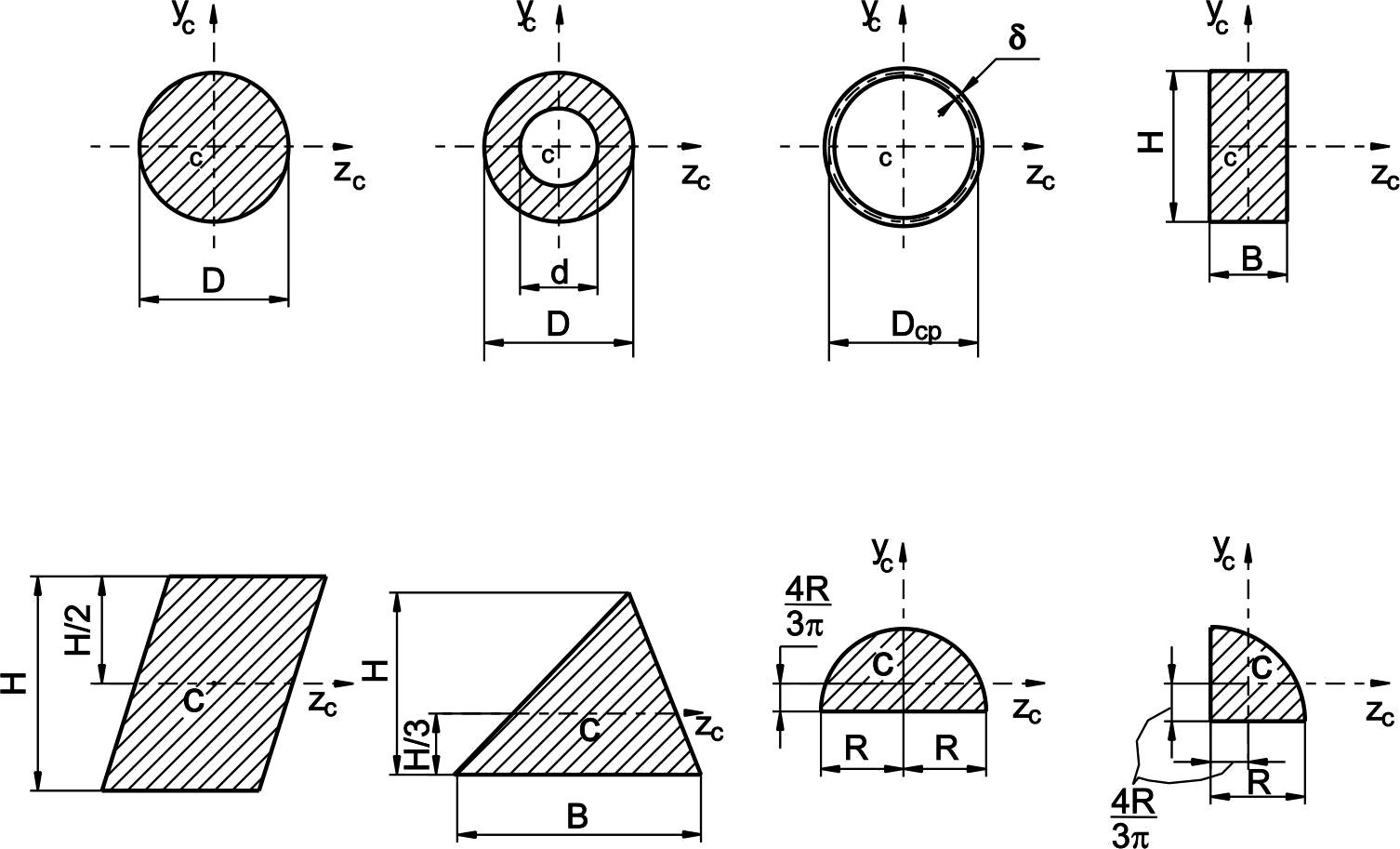
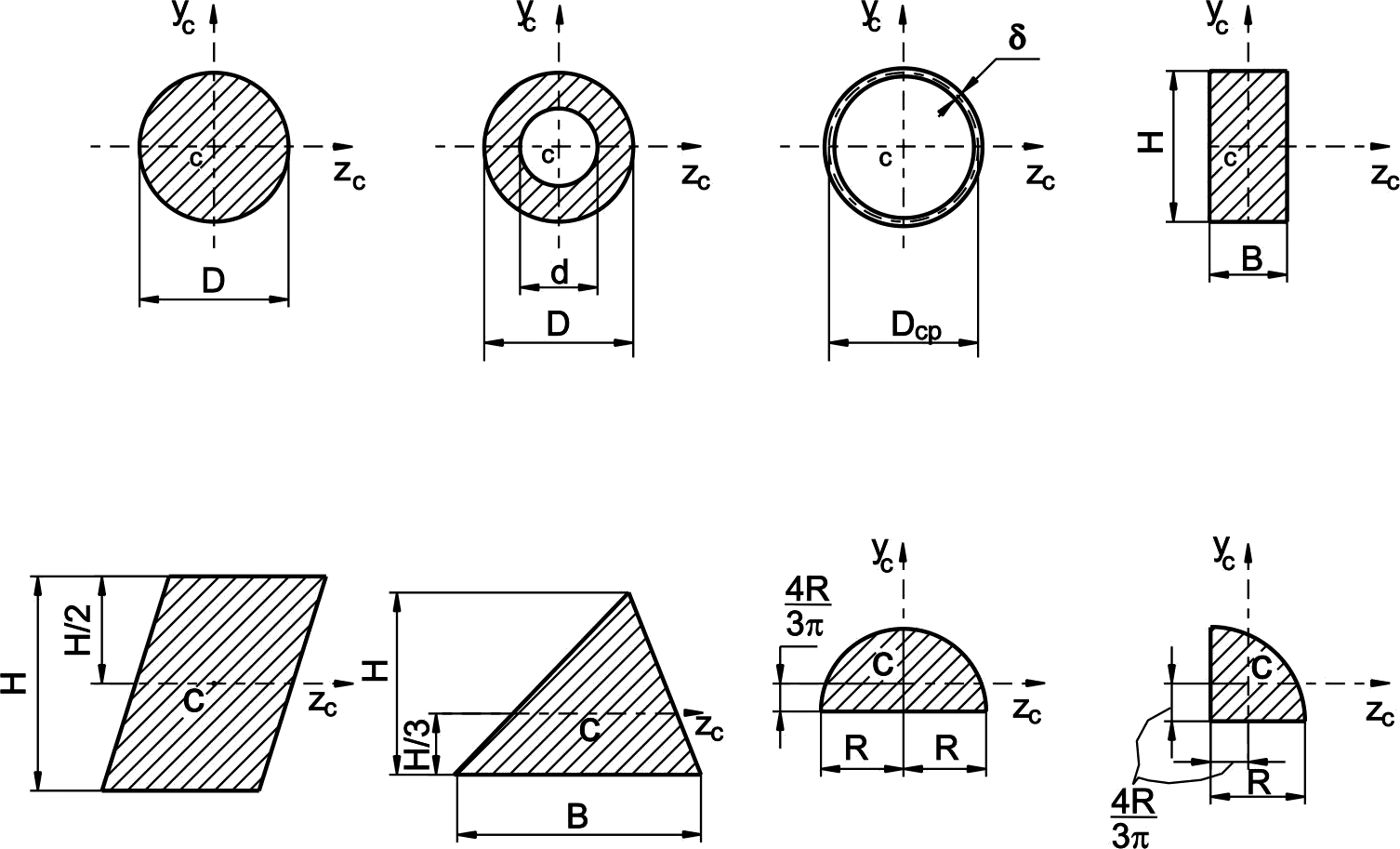
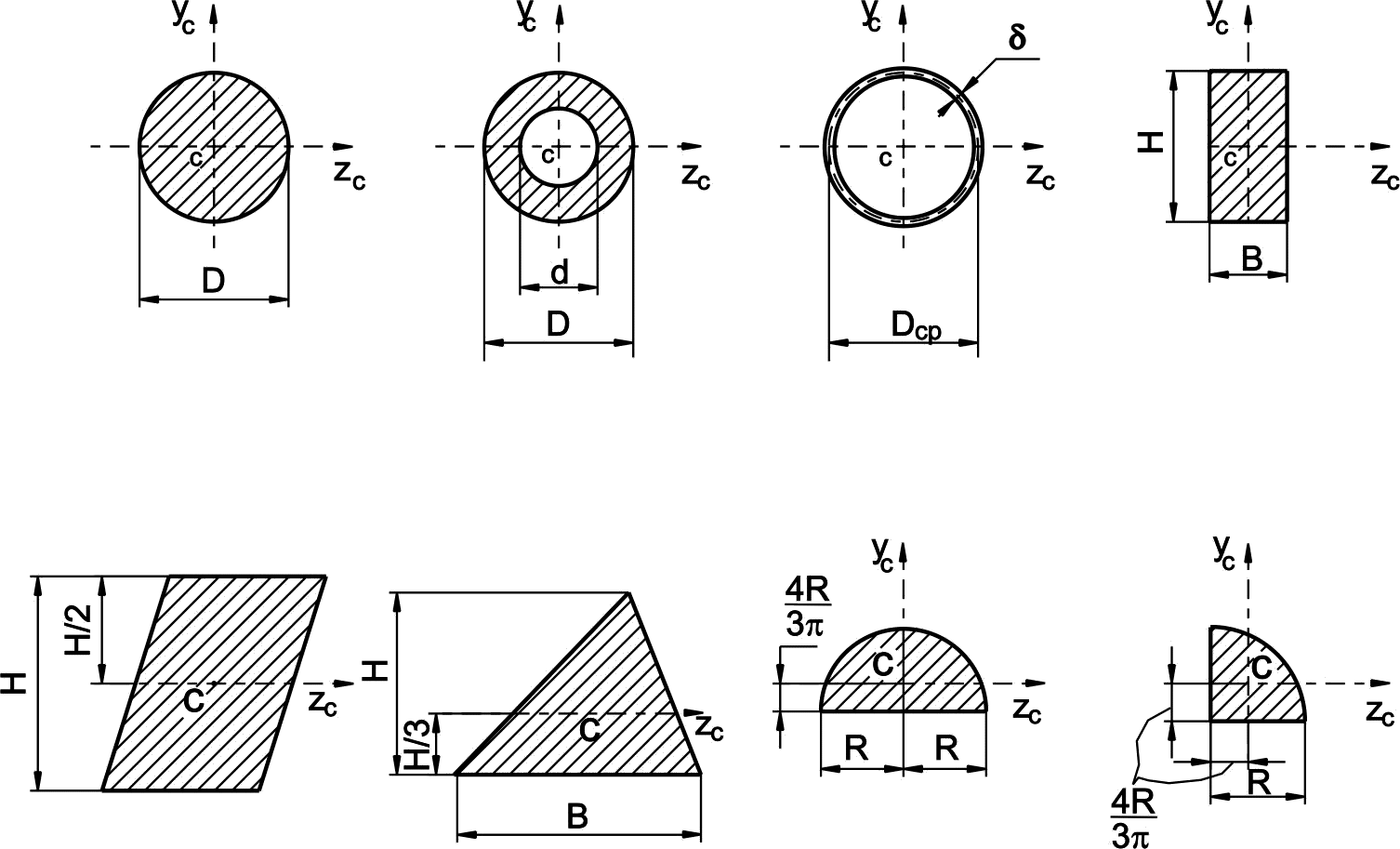
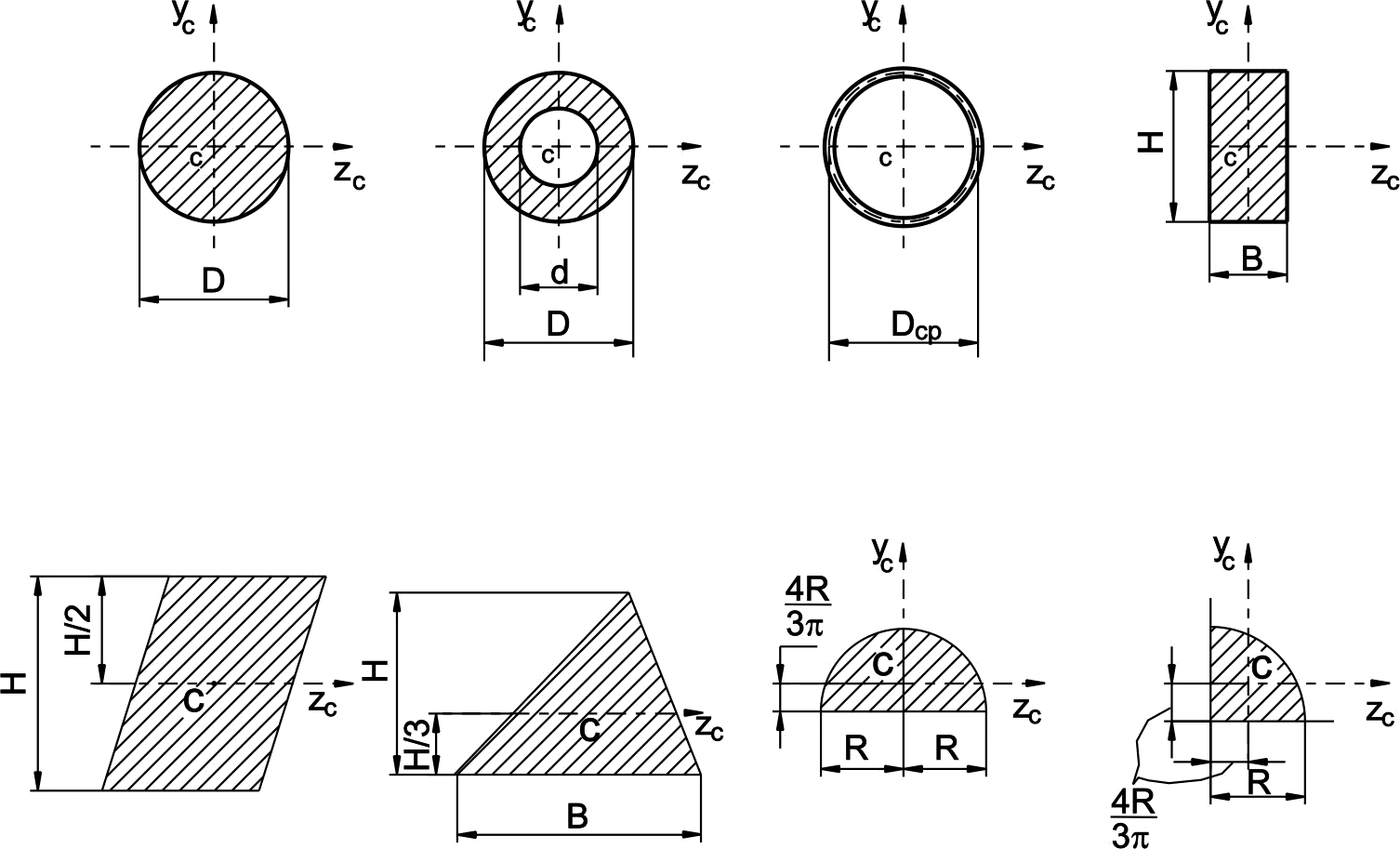
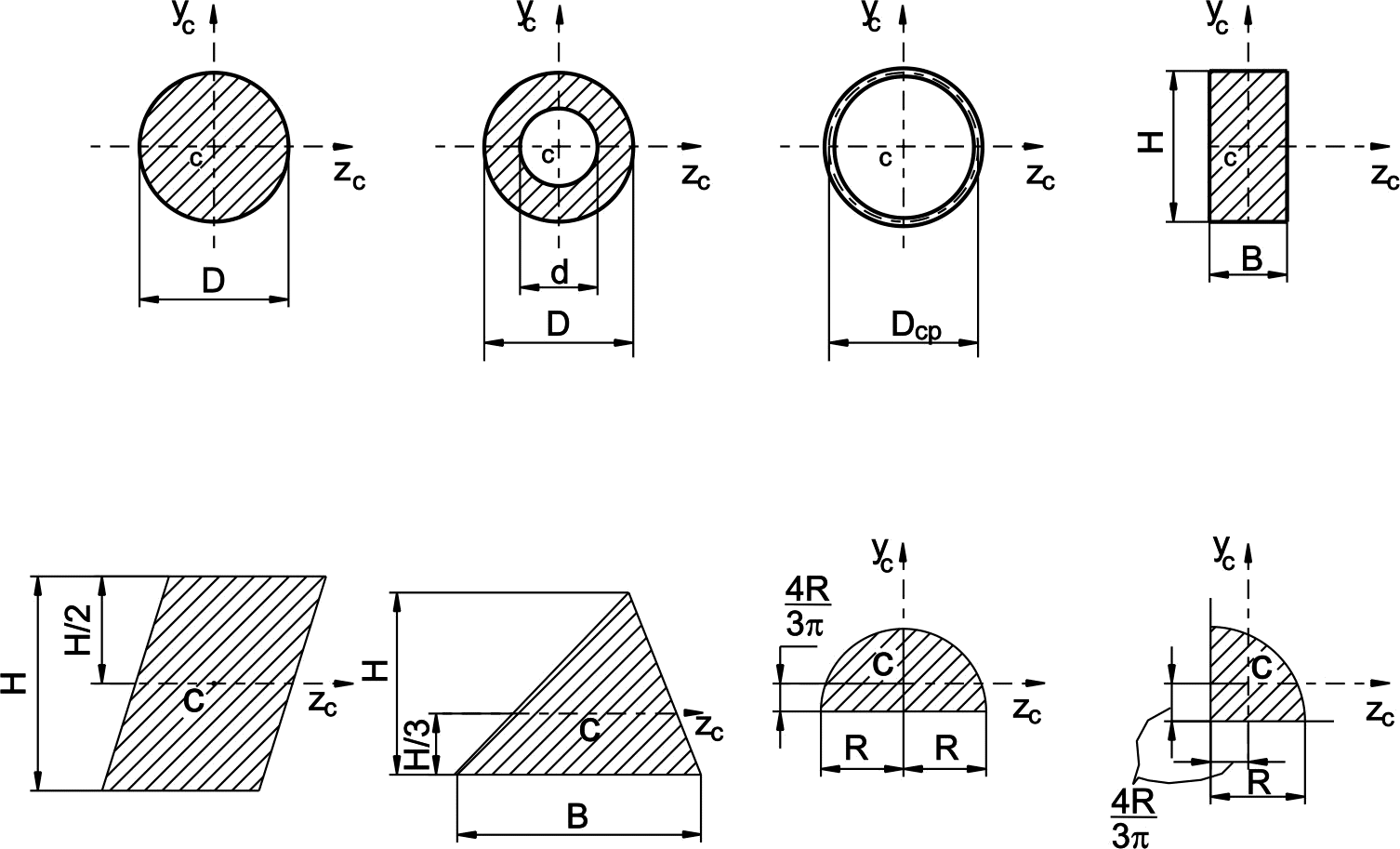
В таблице 1 приведены основные геометрические характеристики некоторых простых сечений с указанием расположения их центра тяжести.
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iПрактическое занятие 1.3
плоское напряженное состояние
При практических расчетах наиболее часто удается определить нормальные и касательные напряжения на некоторых двух взаимно перпендикулярных площадках. Пусть, например, по граням элемента действуют показанные напряжения (рис. 1). Необходимо найти главные напряжения и соответствующие им главные напряжения (Обратная задача в теории плоского напряженного состояния).
Рис. 5
Если обозначить площадки так, как показано на рис. 1, а, то
МПа; МПа;
МПа; МПа.
Определим главные напряжения
МПа
МПа.
Так как значение одного из напряжений получилось отрицательным, его обозначим как .
Тангенс угла наклона главного напряжения к оси
Выполним графическое решение данной задачи.
В геометрической плоскости в системе координат нанесем точку с координатами , (рис. 3.1, б) и точку с координатами , . Соединим точки и

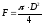 ;
;
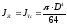

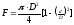
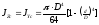
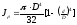
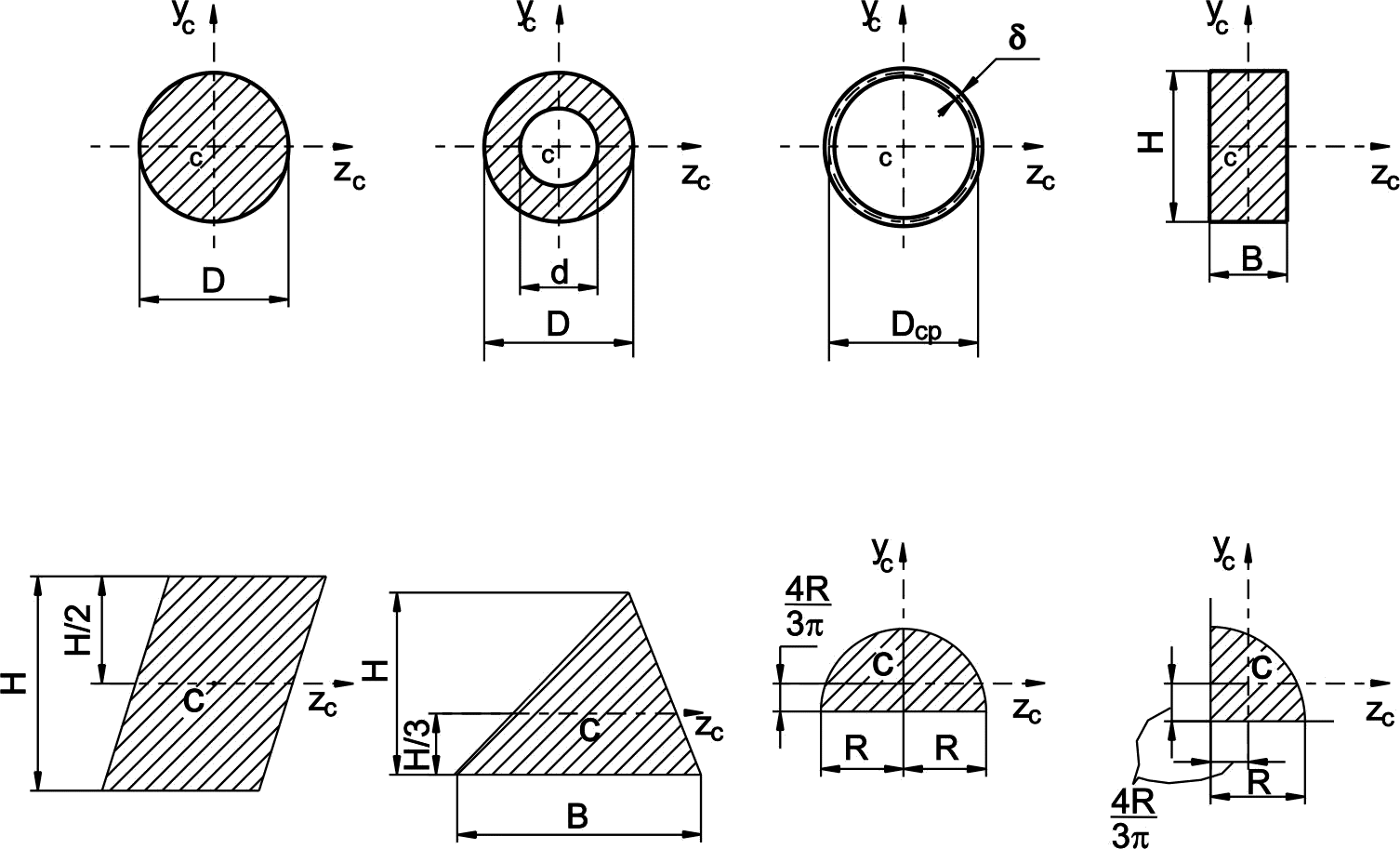
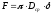 ;
;